�@�@�@�@�@�@�@�@�@����ω��̖@����Бΐ��O���t�Ō��饥�
�͂��߂�
�@���̑O�A�ΐ��O���t���w�K�����B����́A�ׂ����̕ω����w����ɔ�Ⴕ�Ă���ꍇ�������邱�Ƃ������B���������ΐ��O���t�ŕ\���ƁA��Ⴕ�Ă���؋��ɑS�Ē����ɂȂ����B
�@�Ƃ��낪�A����܂ł������Ă����w�����͗��ΐ��O���t�ł͒����ɂ͂Ȃ�Ȃ��B�w�����͕Бΐ��O���t�Œ����ɂȂ�B�����ŁA�����ɂ�������Ă���̂́A���E�̕ω��͔��ɂ���ĕ\����Ă���i�l�Ԃ͔�Ⴕ���F���ł��Ȃ��j�Ƃ������R���炾�B�����āA���̒��̕ω�(�@��)�́A���̂R�̊��ɂ���ĕ\����Ă���B
�i�`�j�ׂ��� �� ���ΐ��O���t�Œ����ɂȂ���B
�@�@�@�@�@�@�@�@�@�@�@�@�@��́A[63,�K���o�[���s�L����]�E�̎��ԃl�Y�~�̎��Ԃ�]�@
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ [65,�x�L������X���[�����[���h��][72,���Ő��E��ǂ݉������Ƃ͂ł��邩]���Q�l�B
�i�a�j�w���� ���Бΐ��O���t�Œ����ɂȂ���B
�@�@�@�@�@�@�@�@�@�@�@�@�@����A[18,�͂܂���̐��w]�@[28,�l�����ׂĂ݂悤]���Q�l�B
�i�b�j�O�p�� �� �|0.1�`0.1�͈̔͂ł͒����ɂȂ���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�U���E���Y���E�J��Ԃ��p�^�[����\���B�t�[���G�W�J�ȂǁB
�@�@�@�@�@�@�@�@�@�@�@�@�@����͕ω����Ă��Ȃ��ƍl���邱�Ƃ��ł���B
�@�����ł͎w������Бΐ��O���t�Ō������āA�O�̓��I�Ɍ��邱�Ƃ����݂Ă݂悤�B
�P�A�o�ς̐��������ŕ\����
[���P]�@�N�ԂP�O�����̌o�ϐ����͂ǂ�Ȋ��ŕ\����邩�B
T�F���Ƃ��A1000�~����P�O�����l�オ�肷��ƁH
S�F1000�{1000�~0.1��1100�~����B�Q�N�ڂ�1100�{1100�~0.1��1210�~�B
S�F1100�~(1�{0.1)��1100�~1.1�̕����ȒP����B
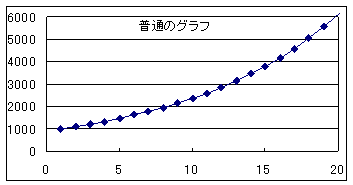
���ԁF�@�@0�@�@�@ 1�@�@�@ 2�@�@ �@3�@�@�@ 4 �@�@�@�@ 5�@�c
�l�i�F�@1000�@1100�@1210�@1331�@1464.1�@1610.51
S�F������O���t�ɂ��Ă݂悤�B
S�F����}�ɏオ���Ă����悤�Ɍ�����B
T�F�Ƃ��낪�����Бΐ��O���t�ŕ\���ƈ꒼���ɕ\����܂��B�Ȃ��Бΐ��O���t���ƒ����ɂȂ�̂��B���̂킯���l���邽�߂ɁA���̕ω������ŕ\���Ă݂悤�B
S�F�ȊO�ɓ���ȁB�w���P�N��10���͂킩�邯�ǁA�w���P���ł͂ǂ��Ȃ�̂��킩��Ȃ���B
T�F�������A�P�O�����̐����̓G�N�Z���ŃO���t��`���Ɩ��炩�Ɉ��̊��ɂȂ��B
S�F����1.1�w�ƂȂ��Ȃ��B
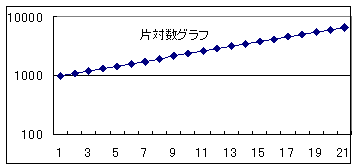
S�F����A��N�Ȃ炢�����ǁA��N�ڂ͂�����܂��g�ݍ��܂Ȃ�����B
S�F�����v�Z����ˁB
S�F��������ƁA�ǂ��������ɂȂ�낤�B
S�F1�N�ڂ́A���z�����{�~(�P�{�N��)������A���̔N�́A(���{�~(�P�{�N��))�����{�ŁA���z��(���{�~(�P�{�N��))�~(�P�{�N��)�ƂȂ��B�Q�N�ڂ������悤�ɍl������B
S�F�������A�܂�A���z�����{�~{(�P�{�N��)�O�^�p�N��}���B
S�F���̏ꍇ���ƁA���z�@����1000�~(1.1^x)
S�F���̏ꍇ�A�^�p�N���ɂ͏��������Ă͂܂�낤���B
T�F�����^�p�N����1.5�N�Ȃ�ǂ��Ȃ�H
S�F1000�~(1.1�O1.5)��1000�~(1.1�O(1+0.5)}��1000�~1.1^1�~1.1�O0.5��1000�~1.1�~��1.1�ƂȂ��Ă����ƌv�Z�ł��邵�A�A���ɂȂ肻������B
S�F�O���t���������̌v�Z�Ƃ҂����荇����B
T�F�悵�A�����10�����̐����̎������������B�ł́A��������N100���ɂ���Ƃǂ��Ȃ邾�낤�H
�Q�A�w�����͑��������̃O���t�ɂȂ�
[���Q]�@�@�N100���̐����́H
S�F���{�~(1�{1.00)^x�����{�~�Q^x���B
S�F���ŏ����ƁA��������Q^x�B
S�F���{���P�Ƃ���ƁA�Q�C�S�C�W�C�P�U�C�R�Q�C�U�S�C�P�Q�W�C�Q�T�U�C�T�P�Q�C�c�Ƒ����Ă����B
S�F���������Ă����Ƃ��̖����̑������ƈꏏ���B
S�F�ۂ��������鎞������ł���B
S�F�������Ea^x�@�͑����������������ɂȂ�ɂȂ��ł��ˁB�������������đ�����ł����H
T�F�������ˁB���̊��͈ӊO�ɑ����A�o�ϐ��������łȂ��A������l���̐����ɂ�������B�˂��ݍu���Ēm���Ă���H
S�F�O�Ƀ`�F�[�����[�����������Ƃ��������B�����̌����̃��X�g���f�����d�q���[���Ɂu���X�g�̂��ׂĂ̌����ɂP,�O�O�O�~���U�荞�݁A���X�g�̈�ԏ�̌������폜���āA���Ȃ��̌�������ԉ��ɉ����ď��ʂ��J��グ�ĉ������B���̐V�������X�g�𑽂��̐l�Ƀ��[���ő��t����A���Ȃ��̌����ɉ��{���̂������U�荞�܂�܂��B�v�Ə����Ă�������B
T�F����͖����A���u�Ƃ����āA���ۂɂ��̂Ƃ���ɑ����Ă����Ǝw�����I�ɑ������A���ォ��ɂ͖c��Ȃ����������Ă��邱�ƂɂȂ�B�����ǁA�����A���u�h�~�@�i�J�ݓ��j���ł��Ė@���ŋ֎~����Ă���B���ꂮ����Ђ�������Ȃ��悤�ɁB
S�F�������l�S�����U�荞�܂Ȃ��Ă����̂����Q�l�̐l���U�荞�炳�����̂悤�ɔ{�X�ɑ����Ă����̂ł��ˁB
S�F����͕K���ׂ����B
S�F���������A�����B���������A�l���͌��肪���邩�疳���ɑ����킯���Ȃ��B��������l���w�����ő�����B
T�F���x�͎w�����Ő��E�̐l���ׂĂ݂悤�B
�R�A�l����Бΐ��O���t�Ō���ƥ���}���T�X�̖@��
[���R]�@�@���E�̐l���́A���N�ق�1.7���̊����ő������Ă����B����́A�ǂ�Ȋ��ɂȂ邩�H
S�F���z�����{�~{(�P�{�N��)�O�^�p�N��}����������A�����ɓ��Ă͂߂�ƁA
�@�l��������Ƃ��̐l���~{(�P�{������)�O�N��}
�@�@�@�@������Ƃ��̐l���~1.017^�N��
S�F�Ⴆ�A1940�N�̐l����2,300,000,000�l�Ƃ���ƁA����2,300,000,000�~1.017^x
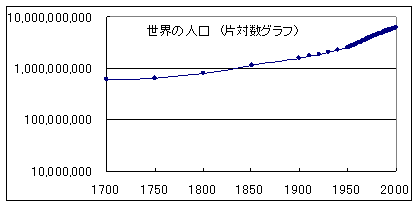
S�F������v�Z����Ǝ��̂悤�ɂȂ�B
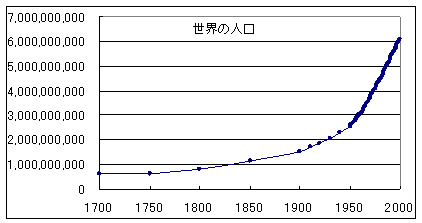
�@�N�@�@�@�@���̒l�@�@�@�@���ۂ̐l��
1940 �@2300000000�@ 2300000000
�@�@�@�@�@�@���
1950�@ 2695658766�@ 2556517137
1951 �@2738789306 �@2594315297
1952 �@2782609935�@ 2636388259
1953 �@2827131694 �@2681738456
1954 �@2872365801 �@2729717908
1955 �@2918323654 �@2781183648
1956 �@2965016832 �@2834158518
1957 �@3012457102 �@2890001400
1958 �@3060656415 �@2946524167
1959 �@3109626918 �@2998875935
1960 �@3159380949 �@3040966466
1961 �@3209931044 �@3081748662
1962 �@3261289940 �@3137743692
1963 �@3313470580 �@3207262725
1964 �@3366486109 �@3278382111
1965 �@3420349887 �@3347361927
1966 �@3475075485 �@3417544528
1967 �@3530676692 �@3487234405
1968 �@3587167520 �@3559028982
1969 �@3644562200 �@3633608846
1970 �@3702875195 �@3708751360
1971 �@3762121198 �@3786142462
1972 �@3822315137 �@3862618859
S�F��̍����Ă��邩�ȁB
S�F�悭�����N������o�����Ƃ��������������ˁB
T�F���̎����o�����}���T�X(1766�`1834)�́A�������̉����𗧂ĂĂ���B�Ⴆ�ΐl�������������ł���Ƃ����������B����ɑ��Đl���������͐l���ɔ�Ⴕ�Č�������Ƃ�������������B
S�F�}���T�X���āu�l���͊����I�ɑ����邯�ǁA�H���͎Z�p�����I�ɑ�����̂Ől����肪������B�v�ƌ������l���ˁB
S�F�l���̑����́A���̐l���ɔ�Ⴕ�Ă���Ƃ����͔̂[���ł���ȁB
S�F���S�����a�������l���ɔ�Ⴗ��Ƃ������Ƃł��傤�B
S�F�w�����́A�����I�ɑ����鎞�������B
S�F�l���̔����I�������ˁB�O���t�ő�����������Ƃ�������B
T�F�ł��A�ŋ߂͑������������X���ɂ���B
S�F�Ƃ���ŁA�u�͂܂����v�ł͊L�̕��ނ��p�x�ł�������ǁA���̐��������g���Γ����悤�ɊL�ނł���Ǝv�����ǁB
T�F�����A�C�f�B�A���ˁB������������Ă݂悤�B�������Ō���L�̕��ނ͂ǂ��Ȃ邾�낤���B
�S�A�L�̐������͏u�Ԃɂ����镪��ʂ̊�����
[���S]�@�L�̐������͂ǂ����߂��炢���̂��H
S�F�L�̎����w���� ��������^�����������B���͌����A�Ƃ͊��ԂƂ��āA���̂��Ƃ����ĉ����낤�H�B
T�Fa�͔N������B�������̕����v�Z�ŁA�@�i���͔N��)
�@�@�@r�i=�������v�j����(1�{a)^t
����́A1�N��1����g�ݍ���Ō������v���o�����̂����ǁA�N��2����g�ݍ��ނƂ���A
�@�@�@������(1+a/2)^2t�@�@�@�c�����͔����ɂȂ��
������������1��̎������������v�͑����Ȃ�B����ɁA�N10��ɂ���A
�@�@�@������(1+a/10)^10t
��������ĉ𑝂₵�Ă����A������g�ݍ��Ƃ���ƁA
�@�@�@������(1+a/p)^pt
�@�@ �@����(1+a/p)^(p/a)at��((1+a/p)^p/a)^at�@�@�@�����ŁAp/a�����Ƃ���B
�@�@ �@����((1+1/n)^n)^at�@���̂Ƃ��A������ɂ���Ƃǂ�ǂ�傫���Ȃ�݂��������ǁA�Ȃ������̒l���ɂȂ�B
�@�@�@ �˂�e^at
S�F�܂�A�N��1�������������ɑg�ݍ��ނ̂ł͂Ȃ��A�A���I�ɑg�ݍ����̒l�Ƃ������Ƃł��ˁB
S�F�������̐������̎��Ɣ�ׂ悤�B
�@�@�@��^ax��(�P�{q)^x�@�Ƃ����
�@�@ (��^a)^x��(�P�{q)^x�@������
�@�@�@��^a��(�P�{q)�@�ƂȂ�A
�@�@���̒l����N����(������)q�����܂邱�ƂɂȂ�B
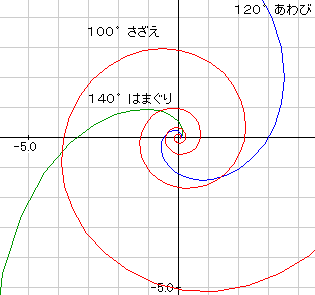
S�F�E�̃O���t�̂悤�ɊL�̊p�x�͂킩���Ă���B�T�U�G��100�x����������A
�@�@�@a��tan(100�|90)��0.176�B�@�@�@��^0.176��1.192
�@�@�@�@ a(�N��)�@�@q(�N��)�@�@ �p�x
�T�U�G�@�@0.176�@�@�@0.193�@�@�@100
����с@�@0.577�@�@�@0.781�@�@�@120
�͂܂���@1.19�@�@�@ 2.29 �@�@�@140
�z�^�e�@�@1.73�@�@�@ 4.65�@�@�@ 150
S�Fa�Ƃ��͂ǂ��Ⴄ�́H
S�Fa�͘A�����ė�����g�ݍ���ł���ꍇ�B���͔N��1��B
S�F�T�U�G�͔N�ԂɁA�������g��19���̊����Ő������Ă���Ƃ������ƁH
S�F�z�^�e���Ă���������������Ȃ��B4�{�ȏ�̊����Ő������Ă���́H
T�F�M�����Ȃ�����C���^�[�l�b�g�Ő����ׂĂ݂��B�P�ʂ͇p�B
�N�@�@�@�F 1�@�@2�@�@3�@�@4�@�@ 5�@�@6�@�@�@����
�z�^�e�@�F 6�@ 10�@ 12�@ 13�@�@�@�@�@�@�@�P�O�`�P�Q�N
�͂܂���F 1�@�@3.2�@�@�@ 4.4�@ 5.5�@�@�@�@�P�O�N
�T�U�G�@�F 2.5�@4�@�@6�@�@8�@�@10�@�@11�@�@�P�O�N
T�F���������ƁA�z�^�e�̐������͑傫�����ǁA�ǂ���w�����Ő������Ă��Ȃ��B
S�F���͑̂̑傫���Ɍ������ăJ���V���E���傷�邩��A�������w�����ɂȂ��Ă���Ǝv���Ă����B
T�F���������v���Ă����B�ȑO�A�\�̐����ׂĂ݂����ǁA�\��(�E���k�̒�����)�w�����Ő������Ă����B�ł��A�L�͎w�����ő傫���͂Ȃ�Ȃ��B�Ƃ��낪�A�`��\�����͎w�����ɂȂ��Ă���B�Ȃ����낤�H
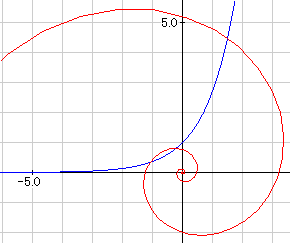
S�F�E�̃O���t�ł����ƁA�Ԃ��点��̎��Ŋp�x�Ƃ������Ɏ��ΐ��O���t�ɂȂ�B�Ԃ͌`�ŁA�͊L�̑傫���������Ă���B
S�F�������傫���Ȃ�A�̐ς͒����̂R��{�傫���Ȃ�B������l����A�w�����ɂȂ��Ă���̂ł́H
S�F���������āA�Ƃ����Ԃƍl����̂����������̂ł́H�B�Ƃ͊p�x�ł���B
T�F�������ˁB�l����o�ς̏ꍇ�́A����������肾�ƁA���鎞���甚���I�ɑ�����B�ł��A�L�͓r���Ő������ɂ߂�B�L�͌o�ςƂ͈Ⴄ�B
S�F���Ⴀ�A�L�̐����̎w�����͉���\���Ă���́H
T�F����́A��f(x)�^��x��f(x)�Ɣ�Ⴕ�Ă���ƍl����Ηǂ��B�L���A����Z�����Ԃ����ɕ��傷��J���V���E���̗ʂ͂�f(x)�B���̊����́A�������g�̑傫��f(x)�ɔ�Ⴕ�Ă���B�������A����𑱂��ĕ��債�Ă���킯�ł͂Ȃ��B�ł��A�`�͏�Ɏ������g�Ɠ����`�ɂȂ�B
S�F�̂̑傫���ɔ�Ⴕ�ĒZ�����Ԃɕ��傷��ʂ����߂Ă��邩��`�͎w�����ɂȂ邯�ǁA������p���I�ɍs���Ă���킯�ł͂Ȃ�����A�����̑傫�����w�����ɂȂ�킯�ł͂Ȃ��Ƃ������Ƃł��ˁB
T�F�������ˁB�����āA�L�̏ꍇ�͐������ł͂Ȃ��A���̏u�Ԃ̕���ʂ̊�����\���Ă���̂�������Ȃ��B
S�F��������ƁAa�̕��̊������g���������ǂ��݂����B�z�^�e��1�N�Ɏ������g��1.73�{�̊����ő傫���Ȃ��Ă���̂ł͂Ȃ��A�������邻�̎��ɁA1.73�{�̊����Ő���(�J���V���E����)���Ă���Ƃ������Ƃ��B
T�F�����āA���̊�����������肾����`�������ɂȂ�B�������Y���y�������ނ������z��ǂ�ł�����A�z�l�K�C(120�x���ɞ�������)�ɂ��Ă���Ȃ��Ƃ�������Ă����B�u���w���g�����邽�߂Ɏז��Ȟ���n�����V�������w�����B����ɂ͂T�`�P�T��������A�H���͂Ƃ�Ȃ��B���̌��ʁA�����Ȑ��͌̍��̂���K�i��ɂȂ�B�v�����āA���̞��܂ł�120�x���Ƃɐ�������B
S�F����ς�L�͕s�A���Ɋk������Ă���B
S�F�ʐ^��������A�T�U�G�ɂ������X�{����ˁB���̞��͈��肷��Ǝז��ɂȂ邩��n�����B�T�U�G�̏ꍇ�͞��܂ō���Ĉ�x�݂���̂��ȁB
S�F�Ƃ���ŁA�ǂ����Ă�f(x)�^������f(x)�Ɣ�Ⴕ�Ă���Ƃ킩��́H
T�F�厖�Ȏ��₾�ˁB���ł����R�ΐ� e�@�̂��Ƃ����ׂĂ݂悤�B
[���T]�@���P�Ō������w������(x)��a^x�̑����̊����A��f(x)�^���������߂Ă݂悤
��f(x)�^������lim[h��0](f(x�{h)�|��(x))�^h
�@�@�@�@�@�@��lim(��^(x�{h)�|��^x)�^h
�@�@�@�@�@�@��lim(��^x��^h�|��^x)�^h
�@�@�@�@�@�@��lim��^x(��^h�|1)�^h
�@�@�@�@�@�@��a^xlim(��^h�|1)�^h
lim(��^h�|1)�^h�@�͂ǂ�Ȓl�ɂȂ�̂��낤���B ��^0��1������A���̒l�́A��^x�̂���0�̎��̐ڐ��̌X���������Ă���B�Ƃ���ŁAlim(��^h�|1)�^h�@���P�ɂȂ�ƂĂ��s�����������ƂɋC�����B��̐}���݂�ƁA�ǂ����X���P�̎��̒l�����肻�����B����͌�ōl����Ƃ��āA�܂��Alim(��^h�|1)�^h�@�̒l�����߂Ă݂悤�B
�����ŁAp����^h�|1�Ƃ����B��^h��p�{1������A�ΐ����Ƃ�ƁAloga(p�{1)��h�@�ƂȂ�B
�����p����lim(��^h�|1)�^h�@��ό`����ƁA
�@�@(��^h�|1)�^h��p�^(loga(p�{1))
�@�@�@�@�@�@�@�@�@ ��1�^((1�^p)�loga(p�{1))
�@�@�@�@�@�@�@�@�@ ��1�^loga(1�{p)^(1/p)�@�@�@�@�@�c�ΐ����ĕ֗��ł��傤�B
����ǂ́A����(1�{p)^(1/p)�̒l���킩���OK�B�����ŁA���̎������܂ōl���Ă������ɒ����Ă݂悤�B
h��0�Ƃ������Ƃ́A��^0��1������p��0�B
�����ŁA1/p�����Ƃ���ƁA
�@�@lim[p��0](1�{p)^(1/p)��lim[n����](1�{1/n)^n�@�@�ƂȂ�B
T�F����͂������o�Ă����ˁB
S�F�����P�ŗ���1/n���O�ɋ߂Â��čs�������̊��Ԗ����̕����v�Z���B
S�F����Ȃ̖�������Ȃ��́H
S�F������0�ɋ߂Â����Ƃ�Y��Ȃ��ŁB
T�F��������߂̎d���������B�����ƔN�����P�ŁA���Ԃ�1�N�B�������A�����������ɑg�ݓ�������Ƃ��鎞�̌������v�B
S�F�v�Z���Ă݂悤�B�����Q�̂Ƃ��͊ȒP���B�ł����Ƃ͂߂�ǂ������ȁB�G�N�Z�����g���Čv�Z���Ă݂悤�B
n�@�@�@�@�@(1�{1/n)^n
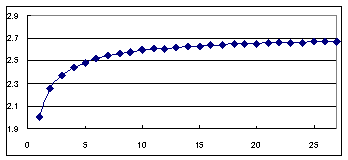
1�@�@�@�@�@2�@�@�@�@�@ =(1+1)^1
2�@�@�@�@�@2.25�@�@�@�@=(1+1/2)^2
3�@�@�@�@�@2.37037037�@=(1+1/3)^3
5�@�@�@�@�@2.48832�@�@ =(1+1/5)^5
10 �@�@�@�@2.59374246�@=
20 �@�@�@�@2.653297705
100�@�@�@�@2.704813829
1000�@�@�@ 2.716923932
10000�@�@�@2.718145927
100000 �@�@2.718268237
1000000 �@ 2.718280469
10000000�@ 2.718281694
100000000�@2.718281786
S�F�Ȃ����̒l�ɋ߂Â��悤�ȁB2.718281�܂ł͊m���݂����B
S�F��(�~����)�݂����Ȑ����B
T�F�����ŁA���̒llim[n����](1�{1/n)^n�����Ƃ���B��������ƁA�������̎���
�@�@lim[n����](��^h�|1)�^h��lim(1�^loga(1�{p)^(1/p))
�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ��1�^loga��
�ƂȂ�A���������āA
�@�@����^x�^��������^x(1�^loga��)
�i1�^loga���j�͒萔������A����^x�^�����͂�^x�ɔ�Ⴕ�Ă���B
����ɁA������ �Ƃ���Aloga����log�������P �ł���A
�@�@����^x�^��������^x
�ƂȂ�B
S�F�o�ϐ����̑����̊������A���̂Ƃ��̑S�̂Ɣ�Ⴕ�Ă���Ƃ��������킩�����B
S�F�� ���Ȃ��o�Ă���̂����킩������B
S�F���͊W�Ȃ��́H
T�F���{������g�傷�邱�ƂɂȂ邯�ǁA���p�点��͊g�債�Ă������ȂB������A��Ȃ̂͂��̒l�I
[���U]�@�]�˂̐������́H
S�F������������A�������̕��@���g���č]�˂̐l�����������o���邩���B
T�F�]�˂̓��p�点��̊p�x��97�`98��������Aa��0.122�`0.141
�@��^a��(�P�{p)�ɑ�����āA
�@��^a��1.13�`1.15��(�P�{p)
�@�܂�Ap��13���`15���@�ƂȂ�B
S�F���́u�N���v���]�˂̐l���������ɂ�����Ƃ����Ă������́H
T�F���ꂪ�l���̑������ɓ�����̂��A�s�s�v��̑������ɓ�����̂��͂킩��Ȃ��B
S�F�ł��A�]�˂̒��̑������͐l���̑������ƌ����Ă������̂ł́B
S�F�������̊L�̏ꍇ�Ɠ����悤�ɍl����A����u�Ԃɂ�����]�˂̒��̕���̊���(����傫�����悤�Ƃ��邿����̊���)���S�̂�12�`14�����Ƃ������Ƃł͂Ȃ��́B
�T�A�w�������Бΐ��O���t�Œ����ɂȂ闝�R
[���V]�@�Ȃ��Бΐ��O���t�Œ����ɂȂ�̂��낤���B
S�F�w�������@����e^ax�@�Ƃ��čl���Ă݂悤�B
T�F�ΐ��O���t�̂����́A�w��(������log ��)�ƍl���Ă悢����A�\�ɂ���ƁA
�@�@x�F�@0�@�@1�@�@ 2�@�@�@3�@�@�@4�@�@�@ 5�@�@�@6�@�@�@7�@���
�@�@y�F�@1�@�@ea�@ e2a�@�@e3a�@�@e4a�@�@e5a�@�@e6a�@�@e7a
log ���F�@0�@�@a�@�@2a�@�@3a�@�@ 4a�@�@�@5a�@�@ 6a�@�@ 7a
S�F��ڗđR�A����log ���͔�Ⴕ�Ă���B�����璼���ɂȂ�B
S�F�����A�Бΐ��O���t�Œ����ɂȂ�����A����͑����������̖@��������Ƃ������ƂȂB
S�F�Ƃ���ŁA�w�����Ƃׂ����Ƃ̈Ⴂ�͉����낤�B
T�F���Ƃ����ʂŌ���ƁA��������Ȃ����ȁB�ǂ������͂��Ⴕ�Ă���B
�@f(x)��a���@�@ ���f(x)�́A���ɔ��
�@f(x)��a��^2�@���df(x)�^dx�́A���ɔ��
�@f(x)��a��^r�@ ���f(x)�́A��^r�ɔ��
�@f(x)��a^x�@�@���df(x)�^dx�́Af(x)�ɔ��
�@f(x)��sin���@ ���df(x)�^dx�́Af(�|���j�ɔ��
�@���Ɂ|0.1������0.1�ł͗��ΐ��O���t�͌X���P�̒����B�܂�Asin���^�����P�ł��邱�Ƃ������ɂ킩��B
�@�����ׂ鎞�ɁA�O���t�\�t�g���g���ƕ֗����B�ΐ��ڐ�����g����O���t�\�t�g���Љ�悤�B
�@�@���y�t�@���N�V�����r���[�z
�U�A(�S���I��)�����̂˂����́A�����Ă�����Y�ɂ���Č��܂�
[���W]�@���̃`���[�g�ɕА��O���t������̂͂Ȃ����H
T�F���ɋ����̂���l�͂��Ȃ������B
S�F�W�F�C�R�����̌딭���̖��͋������������B
S�F����ŁA�����Ɩׂ����l�������ł��傤�B
S�F�Ƃ���ŁA�����̕ω���\���`���[�g�ɂȂ��ΐ��O���t������́H
T�F������l���Ă݂悤�B���̑ΐ��O���t�͕Бΐ��O���t����B�Ƃ���ŁA��������Ă���l�͗��v�⑹���𗦂ōl����B�������z�ɑ��ā������オ�������������������ƂˁB
S�F���~�オ�����Ƃ��ł͂Ȃ��Ƃ������Ƃł����B
S�F���ꂪ�������̐������◘���ɓ�������̂ł��ˁB
T�F���̒l�オ��̋��z�́A�������̐��ɔ�Ⴗ�邩��ˁB������A�o�ό��ۂ��l���鎞�́u���v����Ȃ��āu��v�Ō��Ȃ��Ɩ{���������Ă��Ȃ����Ƃ�����B�����āA���́u��v�ɒ��ڂ����̂��Бΐ��O���t�B
S�F���̔䂪���ɑ������Ă���A�Бΐ��O���t�͒����ɂȂ�܂��ˁB
S�F�t�ɍ������ł��A�傫���Ȃ��Ă����ΐ����͓݂邱�ƂɂȂ�B
�s�F������A�Бΐ��O���t�Œ����I�ɕω����Ă����̂��ς������A�����̕ς��ڂ��Ƃ������Ƃ�����B
S�F�ł����A���̃`���[�g�i���t�[�́j�́A���ʂ̃O���t���Бΐ��̃O���t������Ȃɕς��Ȃ���B
T�F�����ł����̖���������x���グ�悤�B�������͂�������đS�̂Ƃ̔䗦�Ő������l���Ă���B�Ƃ������Ƃ́A�����́u�˂����v���䗦�ōl���Ă���Ƃ������Ƃ��B�Ⴆ�A10���~��1���~���ׂ�Ƃ��ɁA���̐l���ǂꂾ���̍��Y�������Ă���̂��ɂ���Ă˂���������Ă���B
S�F1���~�����Ă���l�ɂƂ��Ă�1���~�ƁA�P�O���~�����Ă���l��1���~�͈Ⴄ�Ƃ������Ƃ��ˁB
T�F�����āA���́u�˂����v�́A�ΐ����g���Ɛ��l�ŕ\�����Ƃ��ł���B
�@���ǂ�