「ベキ関数」から「スモールワールド」へ
１、対数目盛で世界を見る → (空間のスケール)
T：前回、「対数グラフと指数法則」で、対数目盛を学んだね。今度は、このスケールを自然界に当てはめてみよう。
S：対数目盛で自然を計ることができるの？
T：普通の目盛で計るよりも面白いことがわかってくるよ。まずは、いろいろなものを目盛に当てはめてみよう。
微生物(細胞) 昆虫 人間 鯨 社会・生態系 大陸 月
10-4 10-3 10-2 10-1 100 101 102 103 104 105 (ｍ)
─┼──┼──┼──┼──┼──┼──┼──┼──┼──┼──
S：細胞から月まで、同じ目盛に載るんですね。
S：この目盛をもっと大きくすると、どうなるの？
階層 素粒子 原子 分子 生物 惑星 恒星 銀河 泡構造
事物 原子核 水素 分子 微生物哺乳類 地球 太陽 星団
銀河 宇宙
10-20 10-15 10-10 10-5 100 105 1010 1015 1020 1025 (ｍ)
─┼───┼───┼───┼───┼───┼───┼───┼───┼───┼──
法則 量子力学 熱力学 ニュートン力学 一般相対性理論
弱い相互作用 電磁気力 重力
強い相互作用
T：この下に書いてあるのは、当てはまる物理法則なんだ。
S：「ゾウの時間ネズミの時間」の小さな生物は、熱力学の法則の中で生きているというのですね。
S：量子力学とか一般相対性理論なんて、しらなーい。
S：こうやって見ると、この世界は案外狭いなぁ。
T：そうなんだ。私たちが知っているのは、この範囲だけなんだ。
S：それは、対数目盛で見ているからでしょ。
S：そういえば、時間のスケールも同じように考えられないの。
T：そうなんだ。そこで時間のスケールも作ろうと思って始めたけど、この空間のスケールはそのまま時間のスケールにもなることに気がついた。
S：時間にも、最小と最大があるということなんですか？
T：人間の心臓は１00秒で１回動く。ハツカネズミは１０-1、鯨は約１０1。最小はプランク時間１０-43秒で、最大は宇宙の年齢１３６億年≒１０18秒。この目盛は、左が過去で右が現在(未来)のようだ。
S：こうやって見ると、自然には段階があるような気がするな。
T：そうなんだ。自然には階層があり、当てはまる物理法則が違う。だけど、階層を越えた法則はないのだろうか。
S：スケールが違っても、当てはまる法則があるのではないかということ？
S：巻貝の渦は、台風にもあったし、星雲にもあったよ。（はまぐりの数学）
２、対数目盛で関係を見る → (ジップの法則）
T：以前、「エドガー・アラン・ポー」のところで、特別の英語の単語でよく使われるものの出てくる割合について、「ジップの法則」が成り立っているということをやったね。1位がTHE、２位がOF、３位がANDでその頻度は、順位に逆比例するというもの。この分布はフラクタル分布になっている。→（対数グラフ）「ジップの法則」へリンク
表にすると、
出現順位｜ １ ２ ３ ４ …
出現頻度｜ 0.1 0.05 0.033 0.025
S：対数グラフの傾きが-１ということは、指数が-１で、式にすると、ｙ＝0.1χ-1だ。（求め方は「対数グラフ」のページ）
T：こういうｙ＝aχ-1になる関係を、「ジップの法則」という。
S：他にも、この法則に当てはまるものがあるんですか。
T：では、この「はまぐりのサイトの各ページ」のアクセス数を、対数グラフにしてみよう。
| 順位 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 回数 |
24419 |
11153 |
7105 |
5687 |
5124 |
4847 |
4625 |
3849 |
3845 |
3755 |
3646 |
3160 |
S：１位はダントツですね。これ、どのページですか？
T：「アルキメデスは球の体積をどうやって求めたのか」のページですよ。
S：平均的にアクセス数があるわけでなないんですね。
T：そりゃそうですよ。人気のあるページとそうでないページがあって、その割合はだいたい決まっていて、それが毎日合計されるとある一定の割合になるのは当然ですよ。ただ、その毎日の割合がどう決まるのかは不思議ですね。
S：２位は、１位のだいたい半分ぐらいだ。エクセルを動かして、グラフを作り、対数目盛にしてみよう。
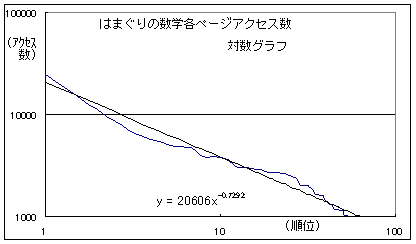
S：この直線は近似値ですか？
T：そうです。エクセルでは自動的に描いてくれます[近似曲線の追加で]。そして、その傾きが-0.7292。
S：直線ではないような…。でも、近いかな。
S：傾きは-1ではないですよ。ｙ＝20606／χ0.73。
T：そうですね。-0.73は-1に近いともいえるけど、違うね。
S：ｙ＝ｙ＝aχ-1ではなく、ｙ＝aχ-0.73だから、「ジップの法則」とは違うけど、これもちゃんと法則だよ。
T：もう一つ、都市別人口なら、インターネットですぐに調べることができるからやってみよう。まず、世界各国の都市別人口を調べてごらん。
S：検索すればいいんだね。なかなか見つからないなあ･･･。あ、「日本の都市別人口のデータ」があった。
| 順位 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 人口 |
8083980 |
3466875 |
2490172 |
2117094 |
1837901 |
1483670 |
1386372 |
1315007 |
1258605 |
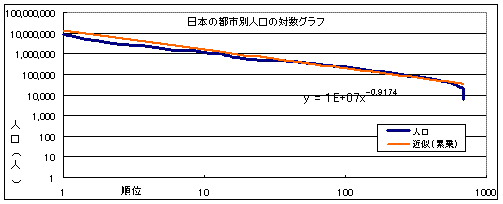
S：これは、かなり、直線に近いね。
S：傾きは−0.9ですね。ジップの法則ではないけれど、ｙ＝10000000／χ0.9という法則が成り立つ。
S：あれ、東京都は1200万人だったんじゃない？
T：この1位の人数は、特別区の人数だけみたいだよ。都市だからね。
S：どうして、直線に並ぶんだろう？不思議だな。さっきのページのアクセス数と同じことが起こっているのかな。
S：ついでに国別の都市別人口も調べてみようよ。
･･･
S：アメリカやロシアのデータが見つかったよ。
S：国によって傾きが違う。人口の多い国ほど傾きが小さくなるような。
S：もしかしたら、人口の多さと傾きは何か関係があるかもしれない。
S：そうだとしたら、すごい発見かも。他の国も調べてみよう。
３、「ベキ法則」と「パレートの法則」
T：このように、自然界には対数グラフで表すと、直線になる関係がとても多い。例えば、地震のエネルギーと回数。ガラスの破片の大きさと個数。月のクレーターのサイズと数、小惑星のサイズと数など。
S：それも「ジップの法則」なんですか。
T：「ジップの法則」は、傾きが-１の場合だけ。この傾きが-0.9や-２や-３になる場合の方が多い。
S：マイナスだから反比例ですね。グラフは左へ行けばいくほど上がる。
T：このように、ｙ＝ａχn（ｎはマイナスの有理数）で表される関係を、「ベキ法則」という。この関係は、自然のスケールに限らずいろいろなところで表れるんだ。
S：対数目盛ではなくて、普通の目盛のグラフを見ると、1位が圧倒的に多くって100位以下はほとんど少ないということですね。
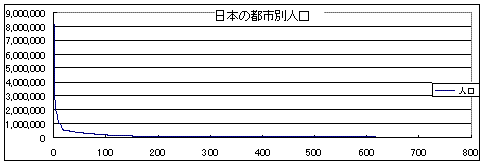
T：そうなんだ。この関係から、面白いことが出てくる。それは、「８０対２０の法則」という。イタリアの経済学者パレートが発見した所得分布の経験則で、全体の2割程度の高額所得者が社会全体の所得の約8割を占める，という法則。
S：そういえばそんな気がするな。金持ちはめちゃくちゃ金持ちだよ。
S：ホントかなぁ。
T：この人口の場合、上位20％の都市が全体の人口の80％を握っていることをいう。
S：本当にそうなるか、エクセルで計算してみよう。
全部で６９１市。上位２０パーセントは138位まで。その合計は66,404,426人だから、全体の合計人数でわると、だいたい65％だ。
S：上のグラフを見ると、パレートの法則が当てはまりそうだけど、８０％もいっていないよ。
S：多いことは多いけど、やっぱり、この法則はいつもいえるとは限らないよ。
T：ところが、パレートの法則はいろいろなところで使用されている。
例えば、
「全商品の20％が80％の売上を作る、全顧客の20％が全体売上の80％を占める、100の蟻の内、よく働くのは2割だけ、税金を納める上位20％が税金総額の80％を負担している・・・」
など。そして、どう使われているかというと、
「商品の品質管理の分野で重点的に改良すべきものを重要なものから順番に10項目あげた場合、まず、その最上位の2つの項目だけを改良する。すると、全体の80％を改良したのと同等の結果が期待できる。」
というように。
S：前に「マンホールのふたはなぜ丸い？」に、「働きアリ」と「怠けアリ」の話があったよ。
『アリの巣を調査した結果、「巣の外にエサを採りに行く」「卵や女王アリをなめてきれいにする」「ごみを捨てる」などの仕事をほとんどしないアリが、どのコロニーにも約２割いた。
働きの良い６匹を取り除くと、次に仕事熱心な層の労働量が若干増えたが、働かない層はやっぱり働かなかった。逆に仕事をしない６匹を除去すると、よく仕事をしていた数匹の労働量は若干、減ったという。』
これは、ニュースに出ていたから、事実でしょ。
S：アリは２割が「怠け者」なんだ。８割は「働き者」。パレートの法則の逆だ。
S：そうすると、会社の２０％の人が、会社の８０％の収入をしているとかいう話も眉唾物だね。
T：こういうときは、エクセルでχが１から100まで、χ1〜χ2の値を計算して確かめるんだ。案外簡単だよ。
S：ｙ＝χ-1では、上位20％が全体の69％。ｙ＝χ-1.2だったら、79.3％になったよ。
S：χの指数が-1.2よりも小さかったら、パレートの法則は成り立つといいうことなの？
T：そう。そして、このことから、ジップの法則もパレートの法則も、ベキ法則の特別の場合ということがわかる。だから、対数グラフを作ってその傾きを調べないと、２割が８割というのはいえないんだ。
S：あるところで成り立つからといって、それを全ての場合に当てはめるのは間違いという事ですね。
S：でも、今まで見てきたデータは、1位がダントツで多いよ。
T：このサイトを見て。→ 【あなたの金持ち度「Global Rich List」】
S：年間収入を入れるんだね。えーっ？。私は真ん中以上だよ。金持ちだよ。
T：今度は、年収１千万円を入れてごらん。
S：ほとんどトップだ。どうして？世界にはもっと金持ちがいるはずなのに。
T：そのわけは、今まで考えてきたことからわかるよ。S：上には上があり、下には下があるということか。でも、大多数の人は貧乏だ。これもベキ法則みたい。
S：もし世界がランダムなら、もっと平均化しているように思うけど、どうして1位（一部）がこんなにたくさん集めるんでしょうか。
T：それについては、次の本を紹介しよう。アルバート=ラズロ・バラバシ著【新ネットワーク思考〜世界のしくみを読み解く〜】という本だ。
４、世界はなぜ平均化していないのだろうか → 【ノードとリンクとクラスター】
T：この本には、「ネットワーク」の「リンク」数が平均化しないで偏りがあり、しかも、ベキ法則に従うのはなぜかということが考察されている。
S：ネットワークって何？リンクって何ですか？
T：世界を、頂点（ノード）と、それをつないでいる線（リンク）でできたグラフと考える。
S：世界ってそんなに単純ではないですよ。
T：複雑な世界を読み解くために、単純化してモデル化し、そこにいろいろな条件を入れながら現実のネットワークの世界を探っていくという方法なんだ。
S：インターネットのサイトや、人と人とのつながりや会社と会社のつながりもネットワークだね。
S：発電所や変電所を頂点（ノード）に、送電線を線（リンク）にすればネットワークができる。
S：脳細胞や神経もそうだよ。木の枝だって、川だって、交通網だってそうだよ。
T：というように、いろいろなものをネットワークとしてモデル化できる。最初は、このネットワークのリンクが、ランダムであるモデルから出発する。
S：ランダムというのはでたらめということでしょ。さいころを転がして決めているということですね。
T：そうやって作ったネットワークでは、現実のネットワークとは違うという事がすぐにわかる。例えば、「世界の誰とでも６人でつながっている」という話がある。
S：世界の誰とでも、知り合いを６人通じればつながるという話でしょ。
T：でも、これはアメリカだけで行った実験らしい。平均すると６人ぐらいで、手紙が伝わったという結果になった。このつながりの回数のことを、そのネットワークの距離という。
S：世界ではないんだ。でも、アメリカで６人だから、世界なら1８人ぐらいでつながりそう。
T：実は、届いた手紙のつながり回数を平均化したのであって、届かなかった手紙も結構多いんだ。
S：世界が、たった６人でつながっているという話ならロマンチックだわ。
T：いずれにしても、なぜ、たった６人でつながっているのかということが問題となる。
S：１人の友人が25人いたら、２５6＝２．４億人でだいたいアメリカの人口になる。つまり、１人が25人知り合いがいたら、６人目でアメリカの全ての人を覆うから、６人でつながるんだ。
S：そんなのおかしいよ。だって、知り合いはたいてい重なっている場合が多いよ。
T：そう。だから、全てがランダムに交わっているというモデルに、リンクの重なりを考慮する必要が出てくる。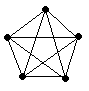
現実は友だちが重なっているので、その重なりぐあいを表現する係数（クラスタリング係数）を導入する。
例えば、私の友人が４人とする。ところが、この友人ネットワークは、リンクが５本しかなかった。
S：私と友だちはつながっているけど、友だち同士では、２人しかつながっていなかったということですね。
T：そう。もし、５人が完全につながりあっているとすると、５（５-１）／２＝１０本ある（左図）。ところが、実際はリンクが５本しかない。このとき、クラスタリング係数Cは、５／１０＝０．５で表される。係数が１になるほど結びつきが強いということになる。これを一般化すれば、あるネットワークがノードをＮ個持っているとすると、
クラスタリング係数＝２（実際のリンク数）／Ｎ(Ｎ-1) で求まる。
S：へー。これ私たちのクラスに当てはめて計算することができそう。
S：クラスが親密であれば、１に近づくということですね。
T：当然、ネットワークがランダムなほど、クラスタリング係数の値は小さくなる。
現実にはこのクラスタリング係数がどれくらいかわからないけど、いろいろな値を設定してモデルでシミュレートすることができる。
５、「ハブ」と「スケールフリー・ネットワーク」
T：アメリカ人のネットワークは２億人もいるのに、つながりの距離は短い。こういうネットワークを、スモールワールド(small-world)という。
(1)
全リンク数が全ノード数の数倍程度しかない、すかすかのネットワークである。
(2)
にもかかわらず、任意の二つのノード間距離がノード数にくらべて著しく短い。
（全ノード数をＮとすると、ノード間距離はlog(N)のオーダー程度）
(3)
また、高度にクラスター化している。
といった性質を合わせて、スモールワールドと呼ぶ。
S：世界は案外狭いということですね。
S：ｌｏｇって指数の逆関数だったね。意味はあまりわからないけど、パソコンの電卓で計算できるよ。
S：ｌｏｇ（２億）＝8.3だし、ｌｏｇ（60億）＝9.8だよ。
S：世界は、9.8でつながっているということなのか。60億人でもそんなに増えていない。比例はしていないよ。
T：ノード数の対数に比例しているんだ。でも、それぞれのネットワークで求める式が違う。例えば、ウェブのノード間距離は、N個のウェブページを持つウェブ上で、ノード間の平均距離をｄとすると、
ｄ＝0.35＋２ｌｏｇＮ となる。
S：クラスターって何ですか？
T：君たちの友人のネットワークのような、頂点（ノード）同士が緊密に塊になっていること。水にだってクラスターがあるんだ。そして、クラスタリング係数はその緊密さの度合いを表している。
S：これで、現実に合うネットワークは作ることができたの？
T：まだまだ。こうやって調べていくと、現実のネットワークには、最初のカウント数のような、特別にリンクの数の多いノードがあることがわかってきた。そういうノードを、「ハブ」（リンクの非常に大きいノードのこと、スケールフリー・ネットワークにしか存在しない。)という。
S：私たちでいうと、中心になっている人のことだね。
T：ところが、スモールワールド・ネットワーク・モデルでは、ハブやベキ法則は現われない。
S：スケールフリーというのは何？
T：前にでてきたような、べき関数（分布）になる性質のこと。
S：上には上があるということか。どうしてスケールフリーというの？
T：放物線のグラフは、みんな相似だったでしょう。同様に、双曲線のグラフも相似になるんだ。つまり、どの部分をとっても同じ形になるから、この部分だと決定できない。だからスケールフリーという。
S：つまりベキ関数は、相似になる性質があるということですね。
T：そして、著者たちが作ったモデルが、スケールフリー・モデル。ネットワークに、「成長」と「優先的選択」という概念を導入することで、ネットワークのスケールフリーを説明できることを示したんだ。
S：ネットワークが常に成長していて、ノードのリンクに優劣があると仮定すれば、べき法則が出てくるということですね。
S：そういえば、お金はどんどん投入されるし、金持ちにお金が集まるリンクが一杯あるからね。
T：しかし、このモデルは、任意の二つのノード間距離がノード数にくらべて著しく短いという性質は持つ一方、クラスタリング係数は小さいのでスモールワールドの性質は持たないらしい。
S：こういうことを研究して何かためになるの？
T：最初に考えたように、世界はネットワークととらえることができるでしょ。例えば、ウイルスの広がりも、ネットワークでとらえることができるんだ。コンピュータ･ウイルスや、エイズ・ウイルスなどがどのように拡散するか、どうしたら収束できるかという研究に役立てることができる。
６、先祖ネットワーク
T：「７５０年前の日本の人口は１０億人！？」という問題がある。この問題を、ネットワークのモデルで考えるとどうなるだろうか。
S：そうか。一族もネットワークだね。しかも、先祖はリンクが２とはっきりしている。
S：子どもは３人ぐらいかな。とすると、平均リンク数は５だ。親子の距離は１、兄弟だと２だよ。夫婦は子どもを通じて２。
S：どこかで、リンクの多いノードがあるし、クラスタリング係数を求めなくては。
S：どんどん成長しているから、スケールフリー・ネットワークとも考えられる。
S：でも、リンクの数はそんなに多くないはずだから、ハブはないよ。（徳川家斉でも５５）
T：もし、先祖ネットワークがランダム･ネットワークなら、平均距離をノード数の関数として予測できる。N個のノードがあり、各ノードが平均ｋ本のリンクを持つとすると、ｄリンクはなれたノードは、ｋd個はNを超えてはいけない。
したがって、ｋd＝N。
よって、ｌｏｇkN＝ｌｏｇＮ／ｌｏｇｋ＝ｄとなる。
先祖ネットワークでは各ノードは５つのリンクを持つから、ｋ＝５。また、ｄとして30代前を設定する。
ｌｏｇＮ／ｌｏｇ５＝３０
ｌｏｇＮ＝３０×０．７＝２１
となり、Ｎ＝１000000000000000000000人となってしまう。これが問題だったんだけど、これを逆に考えてみよう。
まず、江戸時代までの生きていた人数の合計を出す。ボクの計算によると、これが意外なことに1億７千万人なんだ。
（この計算のとき、片対数グラフがとても役立った。）
S：今まで生きていた人すべてをノードにした、先祖ネットワークを考えようというわけですね。
T：そうです。この計算が正しいとして、江戸時代までの子孫ネットワークを考えると、
ｄ＝ｌｏｇ（1.7×１０8）／ｌｏｇ５≒１２となる。
S：これは、江戸時代までの日本の全ての人と、平均１２リンクでつながっているということではないの。
S：先祖が一緒だったりして、さかのぼって下がるということも入れるんだね。
S：でも、これだと時代が下れば下るほど、距離が小さくなっておかしいよ。
T：そうだね。もう一つ、わかっていることがあって、母親を通じて日本人は９つの家系に分かれるという。そうすると、奈良時代までさかのぼれば、生きてきた人の総合計を、ほぼ２億人として、これを９でわると、２千万人。これで計算すると、ｄ＝10.4だよ。
S：９家族の一員だとすれば、平均距離は１０ということなんですね。ほんとかな。
S：９家族という方が驚きだよ。９人に１人はつながっているということの方が。
T：いずれにしても、この先祖ネットワークを、グラフ理論でもっと調べなくっちゃ。
S：いろいろ面白そう。また、研究してみましょう。
参考文献 【新ネットワーク思考〜世界のしくみを読み解く〜】アルバート=ラズロ・バラバシ著
目次へもどる