対数グラフと指数法則

――　　ｙ＝χ²　も　ｙ＝√χ　も　ｙ＝1／χ　も同じ直線のグラフになる世界　――

問題１　無限小を表す目盛はないの？　･･･「数直線目盛」と「対数目盛」

T：普段、私たちは数直線をグラフの目盛に使っている。このような正負の目盛って、どういうときに使うのかな？
S：温度を表わすときには便利だよ。それ以外は、えーっと･･･。

　-5　　　-4　　　-3　　　-2　　　-1　　　0　　　　1　　　　2　　　 3　　　 4　　　　5　　　 6　
─┼──┼──┼──┼──┼──┼──┼──┼──┼──┼──┼──┼──

T：温度も、絶対温度で表せばマイナスは必要ないよ。実際、世界をよく見ると、マイナスはあまりないんだ。だけど、０に近いところはたくさんある。
S：そうか、私たちの世界は正負よりも、無限大と無限小ですよね。だから、負の数よりも、０に無限に近づく目盛が必要ですね。
S：細菌や分子や原子、そして素粒子の世界と、どんどん小さくなっているもんね。
T：そうなんだ。それで、紹介するのが「対数目盛」。どういうグラフか、実際に調べてみよう。
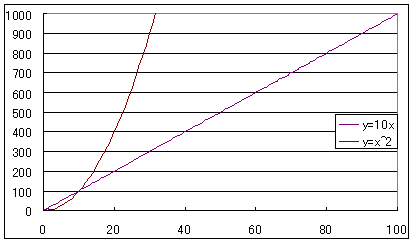
(1)まず、エクセルを起動して。それからχとして、１〜１００までを縦に作る。
(2)次に、その横にｙ＝１０χとｙ＝χ²を作り、χの値に対応するｙの値を計算させる。
(3)そして、それをグラフにする。【グラフの種類】は【散布図】。範囲指定をすると、下のグラフができる。
S：正比例と二次関数のグラフだね。

エクセルのグラフ１

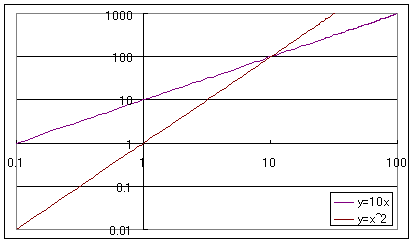
(4)ここで、目盛を対数目盛に変えるよ。まず、ｙ軸の数字をクリックして、印が出たら右クリックする。すると、【軸の書式設定】と出てくるので、クリックして【目盛】を選ぶ。下の方に【対数目盛を表示する】と出てくるのでチェックを入れ、OKとクリック。
(5)これを、χ軸でも同じように行う。できたのが次のグラフ。

対数目盛のグラフ２


問題２　なぜ直線になるの？

S：あれ、二つとも直線になったよ。どうして？二次関数は放物線を描くはずだよ。なぜ直線になるの？
S：直線になるということは比例しているということでしょ。二次関数は比例じゃないよ。
T：よし、なぜ直線になるのか調べてみよう。まず、このグラフのχ軸の目盛を見て。
S：１，１０，１００だ。次は１０００だな。
S：左は0.1だから、次は0.01かな。つまり、こうなっている。

　　0.0001　 0.001　 0.01　　0.1　　　1　　　10　　 100　 1000　 10000　 100000 ・・・
　　─┼──┼──┼──┼──┼──┼──┼──┼──┼──┼──

S：ｙ軸も一緒だよ。ところで、０はどこにあるの？
S：０は、左の方にどこまで行ってもないよ。
S：えーっ。
S：それに、間隔が一定ではないよ。０に近い方がどんどん拡大されている。
S：どんどん小さくなるけど、０にはならないんだ。
S：小学生のころ、少数のかけ算は大きくならずに小さくなったことが不思議だったことを思い出すよ。
S：そういえば、この目盛は大きい方を0.1倍してできている。

問題３　この目盛のしくみはどうなっているのか？　　・・・指数法則

T：さて、この目盛を調べるために、これらの数を指数で表してみよう。
S：100＝10²　にするということ？
S：1000＝10³，10000＝10⁴・・・。でも、１＝はどうするの？
S：0.1＝1／10，0.01＝1／10²・・・だね。規則があるような、ないような。
T：今出た疑問は、指数の法則を調べれば解けるよ。
S：指数法則って、ａ²×ａ³＝ａ⁽²⁺³⁾　というの？
S：もう一つあったよ。ａ⁵÷ａ³＝ａ^(5-3)　だよ。
S：かけ算は＋に、割り算は−になるのはどうしてなの？
S：(ａ×ａ)×(ａ×ａ×ａ)＝ａ⁽²⁺³⁾＝ａ⁵　だから。
S：(ａ×ａ×ａ×ａ×ａ)／(ａ×ａ×ａ)＝ａ^(5-3)＝ａ²　だから。
S：引き算ができるということは、ａ²÷ａ²＝ａ^(2-2)＝ａ⁰だよ。
Ｔ：いい考え方だね。つまり、左辺は１だから、ａ⁰＝１となるよ。ａ⁰をかけることは、指数に０を足すことで、ａ⁰で割ることは、指数から０を引くことだから、その値は変わらないね。
S：ａを０回かけると１というのは、なんかおかしいな。
S：ａ×0.3だって、ａを0.3回足すというのはおかしいでしょ。でも、ａ×3／10＝（ａ＋ａ＋ａ）／10と考えればいいでしょ。
S：ということは、ａ⁰＝ａ¹／ａ¹＝ａ²／ａ²…と考えればいいわけか。
S：ａ⁰＝１なら、マイナスの指数も考えられるよ。
S：そうだよ。ａ²÷ａ³＝ａ^(2-3)＝ａ^-1　だ。これって正しいの？
T：左辺を計算すると？
S：１／ａです。そうすると、ａ^-1＝１／ａということ？
Ｔ：これが正しいかどうかは、指数法則に当てはめてみればわかるよ。
S：(ａ^-2)×(ａ^-3)＝ａ^(-2-3)＝ａ^-5＝１／ａ⁵
S：左辺を分数にしても、ぴったり合っているよ。ａ^-n＝１／ａⁿ　と考えてもいいんだ。
S：ということは、さっきのグラフの目盛は、全部指数で表せるということですね。

　　　　10^-4 　 10^-3　　10^-2　　10^-1　　10⁰　　　10¹　　10²　　　10³　　10⁴　 　10⁵　…
　　　─┼──┼──┼──┼──┼──┼──┼──┼──┼──┼──
　　　　-1　　　-3　　　-2　　　-1　　　0　　　　1　　　　2　　　3　　　　4　　　　5　　（指数だけを取り出す＝対数）

S：指数だけ見ると、数直線と同じだ。
T：そうなんですよ。ここで指数だけを取り出すんです。そうすると、数直線の目盛と同じになる。
S：でも、計算がおかしくならない？
T：さっきの指数法則をもう一度見て。これは、左側がかけ算(割り算)で右側は足し算(引き算)になっている。つまり、指数を使うと、かけ算を足し算にできるんだ。さらに、指数にかけ算も定義することができる。例えば、Y＝X²で、X＝10³を代入すると、Y＝(10³)²＝(10³)×(10³)＝10^(3×2)＝10⁶　となる。つまり、かけ算は足し算に、累乗はかけ算にできるんだ。これを表にすると、

X｜10⁰　10¹　10²　10³　10⁴　10⁵　 10⁶
Y｜10⁰　10²　10⁴　10⁶　10⁸　10¹⁰　10¹²　　　このようになる。

S：あれ？指数だけを見ると、XとYが比例しているよ。比例定数は２だ。
T：そうなんです。ということは、この指数の目盛でグラフを作るとどうなるだろうか。
S：そうか！　それで、直線になっているのか。
S：だったら、ｙ＝χ³のグラフは傾きが３になるはずだよ。
S：指数がマイナスのグラフの場合は、どうなるのかな。
S：反比例のグラフは、ｙ＝１／χ＝χ^-1だから、これも直線になるの？

問題４　ｙ＝１／χ＝χ^-1のグラフはどうなるか？

エクセルのグラフ３

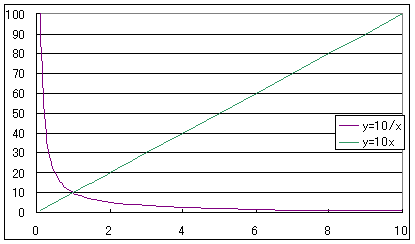
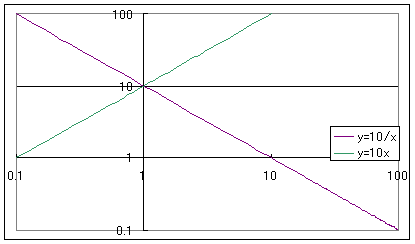
S：ちゃんと直線になっているよ。しかも傾きが−１の直線だ。
S：ということは、二乗に反比例する関数など、みんな直線になるということですね。
S：ｙ＝１／χ²や１／χ³・・・のグラフも作ってみよう。

問題５　ｙ＝１／χ²や１／χ³のグラフはどうなるか？


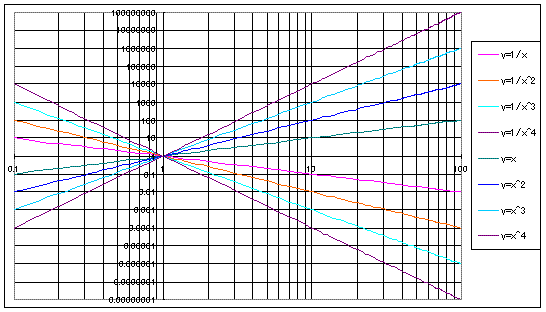
S：ｙ＝１／χ²＝χ^-2，１／χ³＝χ^-3　だから、傾きが、それぞれ‐2，‐3になっているね。
S：ということは、指数の世界から見ると、比例も、反比例も、二次関数・三次関数も、みんな同じｙ＝χⁿの(ベキ)関数ということですね。
S：でも、一つ疑問があるんだ。整数についてはわかったけど、この10⁰から10¹の間はどうなっているの？
T：いい質問ですねえ。考えてみましょうよ。

問題６　10⁰から10¹の間は、どうなっているのか？　　・・・有理数の指数

　10⁰　　　　　　　　 10¹　　　　　　　　10²　　　　　　 　　10³　
─┼──────┼──────┼──────┼─

S：０と１の間だから、きっと0.1とか0.2の指数があるんだ。
T：いい着眼点だね。そのとおり。少数の指数がある。
S：でも、指数が少数だなんて、どうやって累乗するの？
T：実は、この少数の累乗の計算については、もうみんなは知っているよ。
S：まさか√じゃないよね。
T：そう。そのまさかなんですよ。まず、10^0.5＝10^1/2を考えてみよう。さっき、(10³)²＝(10³)×(10³)＝10^(3×2)と計算したでしょう。ということは、100^1/2=(10²)^1/2＝10^(2×1/2)＝10¹＝10。
S：わかった。1/2乗は√と同じだ。だって、√(10²)＝10だよ。
T：そのとおり。同様に1/3乗や1/4乗も考えることができる。
S：ａ^1/3は、３乗したらａになる数。1/4も同じように考えられる。
S：そうすると、0.1乗は1/10乗と考えれば良いのか。
S：10^2/3も定義することができるよ。(10²)^1/3と考えればいい。
S：グラフの傾きも2/3になるよ。
T：こういうように、指数を有理数にまで拡げることができる。もちろん実数にも、さらには虚数にも。そして、こうやって拡げていくと、比例・反比例・二次関数だけでなく、無理関数や三角関数まで指数で表すことができるんだ。
S：指数関数って、「はまぐりの成長」で出てきた関数でしょ。不思議な関数だな。
S：そうか。わかったぞ。ｙ＝aχ^rが直線になるということは、これらは全て「χ^rに比例している」からだ。
T：そうです。だからこのグラフを使うと、自然界のさまざまなモノ・コトの間にある法則を見つけ出すこともできます。
S：対数グラフが直線になれば法則があるということですね。

0　　　　　0.1　　　　0.2　　　　0.3　　　　0.4　　　　0.5　　　　0.6　　　　0.7　　　　0.8　　　　0.9　　　　　1
10⁰　　　 10^0.1　　　10^0.2　　　 10^0.3　　　 10^0.4　　　 10^0.5　　　 10^0.6　　　10^0.7　　　 10^0.8　　　 10^0.9　　　10¹
┼───┼───┼───┼───┼───┼───┼───┼───┼───┼───┼
1　　　　　1.25　　　1.58　　　1.99　　　　2.51　　↑3.16　　　3.98　　　5.01　　　 6.31　 ↑ 7.94　 ↑　10
１　　　　　　　　　　　　　　　　　２　　　　　　　　　３　　　　　　　４　　　　５　　　　６　　　７　　 ８　　９　１0

T：上の(問題５)のグラフを見ると、χ軸の補助目盛が描いてあるよ。
S：あれ？等間隔ではないですね。これは何を表しているのですか？
T：これは指数ではなく、２，３，４，…です。実際にグラフを作るときはその方が描きやすいからね。
S：次は、20，30，40，…ですね。
S：ところで、なぜ指数グラフといわないで、対数グラフというのですか？
T：１や２や３を、10^xで表すと、χはいくつだろう？
S：10^x＝２になるχですね。
Ｔ：この指数χの方を求めたくなるよね。それが対数（１０を底として、２に対する指数）なんだ。
S：関数　ｙ＝10^x　の逆関数ですね。
Ｔ：この場合、χ＝ｌｏｇ２＝0.3010299956639811952137388947244…となります。
S：つまり、指数の目盛で約0.3のところが、２ということなんですね。

T：さあ、このグラフを使って世界のしくみを読み取ってみよう。
私たちは、お金も対数目盛で考えている。

目次へもどる