S:9は一番最後に現われるから、損だよ。
S:こういう場合、確率は平均値になるのかな。
S:ということは、それぞれの確率は違うということではないの。
3、確率をグラフにすると
T:これをグラフにしてみよう。まず、1と2の場合だけ。

S:桁数が1つあがると、グラフが伸びるよね。0から10までの間がわかりにくいな。
S:確率は桁が1つ上がると、同じ繰り返しになる。1〜10〜100〜1000〜10000と相似になっているはず。
T:それなら、χ目盛を対数目盛りにしてみよう。
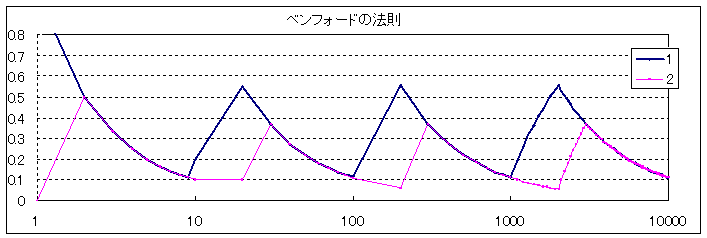
S:同じ曲線が繰り返すよ。対数目盛りだから、当然か。
S:1の方が2よりも確率が大きいよ。
S:1の方の平均は0.3ぐらいだ。2の方は0.2ぐらいかな。
T:では、この確率を具体的に求めるにはどうしたらいいのだろう。
S:このグラフを見ると対数と関係があるような気がする。
T:そうだね。10のn乗がポイントかもしれない。
4、確率を求める
T:どうしたら具体的な確率が求まるのかな。
S:この曲線を積分してやればいいのではないの?
S:でも、この曲線の式はわからないよ。
T:対数ということは、指数で考えたらどう。まず、ある数を指数10αで表わす。
S:どうして?
T:その方が便利だからね。
例えば103.5=100.5+3=100.5・103 (103が桁数を表わし、100.5が数値を表わす。)
この100.5の整数部が最高位の数ということになる。
桁数の方は考えに入れなくてもいいので指数の整数部分は無視し、小数部分だけを調べればいい。
もちろん小数部分は0〜1までの数をとり、どれも一様に出現する。
では、指数の値によって整数値はどんな数になるのか。
S:100=1 100.3010=2 100.4771=3 100.6020=4 100.6990=5 100.7781=6 100.8451=7 100.9030=8 100.9542=9 101=10
そうか!わかった!この指数の幅から確率を求めることができるぞ!
1になるのは、100~0.3010 0.3010−0 =0.3010
2になるのは、100.3010~0.4771 0.4771−0.3010=0.1761
3になるのは、100.4771~0.6020 0.6020−0.4771=0.1249
4になるのは、100.6020~0.6990 =0.0970
5になるのは、100.6990~0.7781 =0.0791
6になるのは、100.7781~0.8451 =0.0670
7になるのは、100.8451~0.9030 =0.0579
8になるのは、100.9030~0.9542 =0.0512
9になるのは、100.9542~1 =0.0458
S:ということは、対数目盛の間の長さが確率と言うことですね。
S:でもね、この場合、10x=yとすると、xの分布とyの分布は違うよ。この場合はxの分布をとったけど、yのT分布をとると確率は1/9になるよ。指数xの分布を確率に選んだ理由はあるの?
T:大事な疑問だね。ここで、xの分布とyの分布を比べてみよう。xの分布は下の図の様になる。
Log2 Log3 Log10
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1
100 100.1 100.2 100.3 100.4 100.5 100.6 100.7 100.8 100.9 101
┼───┼───┼───┼───┼───┼───┼───┼───┼───┼───┼
1 1.25 1.58 1.99 2.51 ↑3.16 3.98 5.01 6.31 ↑ 7.94 ↑ 10
1 2 3 4 5 6 7 8 9 10
S:この図で、yの分布は数直線の下で、xに合わせると均等(一様)ではなくなる。
T:さて、この二つの分布の違いは何なのか。
yの分布を、 1 2 3 4 5 6 7 8 9 と一様に並べ、2倍してみよう。
すると、 2 4 6 8 10 12 14 16 18 となり、最高位の桁が1であるのが5倍に増える。
これは、yの分布が乗法に対して一様ではない(縮尺不変ではない)ということを示している。
それに対して、xの分布を2倍すると、
(指数x) (数) (2倍の数)
0.1 100.1(=1.26)×2=100.1×100.301=100.1+0.3=100.401=2.52
0.2 100.2(=1.58)×2=100.2×100.301=100.2+0.3=100.501=3.17
0.3 100.3(=1.99)×2=100.3×100.301=100.3+0.3=100.601=3.99
0.4 100.4(=2.51)×2=100.4×100.301=100.4+0.3=100.701=5.02
0.5 100.5(=3.16)×2=100.5×100.301=100.5+0.3=100.801=6.32
0.6 100.6(=3.98)×2=100.6×100.301=100.6+0.3=100.901=7.96
0.7 100.7(=5.01)×2=100.7×100.301=100.7+0.3=101.001=10.02
0.8 100.8(=6.31)×2=100.8×100.301=100.8+0.3=101.101=12.62
0.9 100.9(=7.94)×2=100.9×100.301=100.9+0.3=101.201=15.89
となって、2倍する前は3個、2倍しても3個で変わらない。これは、上の数直線を右へ0.3だけずらした時、1の幅は10の幅に移り、合計の長さは変わらないことからもわかる。このようにxの分布は乗法に対して一様(縮尺不変)になっている。
また、指数xは桁数を表しているから、桁数xの方がyよりも一様になっているということがわかる。
S:でも、なぜ乗法に対して変わらない分布の方が良いの?
T:長さ、重さなどの数の集合は、単位が違っても最高位の桁の分布が同じでないと困る。もし、単位が違うたびに分布も違ってくると、分布の法則はないことになる。指数xの分布だと単位が違っても1の分布は同じになるので、指数xの分布で確率を考えた方がいいのだ。
よって、この指数を対数の式で表わすと、次のように確率を求めることができる。
最高位の数がnになる確率P(n)=(Log10(n+1)-Log10n)/(Log1010-Log101)
=(Log10(n+1)-Log10n)
=Log10((n+1)/n)
=Log10(1+1/n)
これをベンフォードの法則という。(1938年発見)