比例の表から対数目盛りの表へ
ここでは、計算尺の原理を「比例の拡張」という視点から再構成してみます。
【表アイテム】でやったように、「表」を使うと、比例(かけ算)が目に見えるように表わされます。
例えば、×2は次の表で表わされます。
0 1 2 3 4 ・・・ 9 ・・・ 100・・・
0 1 2 3 4 5 6 7 8 ・・・ 18 ・・・ 200・・・
でも、これだと3倍、4倍の表を作るには、3の段の目盛り、4の段の目盛りを作らなければなりません。
だから、一つの目盛りで全てのかけ算ができればとても便利です。
でも、そんなことができるのでしょうか。
実はできるのです。そして、そのためのポイントはただ一つ。「ずらす」ことができるということです。
ところが、比例の表は、「ずらす」と一次関数になってしまいます。
この問題点を克服するにはどうしたらいいのでしょう。
(1)まず、「比例の表をずらすと比例でなくなるのは、なぜか」を考えてみましょう。
┌ ×2┐ ┌ ×2┐
0 1 2 3 0 1 2 3
0 1 2 3 4 5 6 7 0 1 2 3 4 5 6 7 8
└ ×2┘ └×1.5┘
×2 ×1.5 ×1.33 …
1 2 3 4
このように比例の表は隣の数との比が一定ではないので、ずれると比例ではなくなるのです。
つまり、表が等差数列になっていて、等比ではないことが原因なのです。
とすると、同じ倍率を同じ長さ(等比数列)にすれば、ずらしても比例になるのではないかと予想できます。
前の数の2倍なら次の数も2倍にするのです。
1 →×2→ 2 →×2→ 22 →×2→ 23
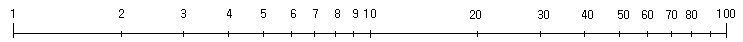
1 →×3→ 3 →×3→ 32 →×3→ 33
このように、2倍の数の間隔が常に一定になっていたら、ずらしても比例になっているはずです。
これは、等比数列(指数)の表を使うということです。
(2)では、等比数列(指数)で表を作ってみましょう。
20 21 22 23 24 25 26
20 21 22 23 24 25 26
この表は、もちろん比例しています。指数も比例していますね。
では、この表を「ずらして」みます。
20 21 22 23 24 25 26
20 21 22 23 24 25 26
指数を見ると一次関数ですが、値は確かに比例しています。
なんと「ずらして」も比例関係が保たれているのです!
ですから、この表を使うと、【表アイテム】と同じ様に計算(かけ算)ができることになります。 (ex. 22×23=22+3=25)
さらに、20=30=40=1ですから 30 31 32 34 35・・・も同じ数直線上にのせることができます。
こうやって作った数直線が対数目盛なのです。
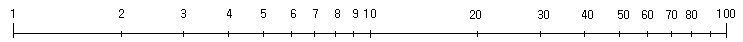
20 21 21.58 22 22.32 23
0 1 1.58 2 2.32 3 (目盛の長さ)
この目盛は、長さを指数で決めます。
例えば、3=2xとしてxを求めると、それが2を1とした時の3の長さということになります。
このxを求めると、1.584962501…となります。
指数で表すときは、何を基数(底)とするのかが問題となります。この場合、基数2が単位みたいなものです。
(3)2つの対数目盛を「ずらして」みましょう。

見事に比例関係が保たれていますね。しかも、下の表は上の表の2倍になっています。
もっと「ずらして」みましょう。
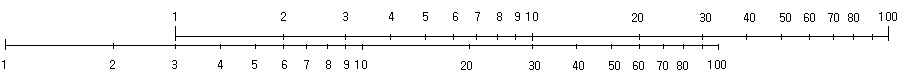
上が2倍になれば、下も2倍。3倍になれば3倍です。そして、上の表の3倍が下の表の値になっています。
これを利用すると、かけ算が簡単にできることに気がつきます。
そして、もっと細かい目盛りを使えば、1.5×3.6も簡単に計算できます。
ずらすことは加法減法です。ずらしても比例になるということは、乗法除法ができるということです。
乗法が加法に変わります。これが計算尺の原理です。
なぜ比例するのかは、【64、対数グラフ と
指数法則】のページへ
等比数列と等差数列の違いについては、【67、私たちは、お金を対数目盛で考えている!?】のページへ
目次へもどる