1、九九の表でベンフォードの法則を調べる
ベンフォードの法則によると、最初の桁は1になる頻度が高い。 九九の表でも同じことが言えるのだろうか。×|1 2 3 4 5 6 7 8 9
1|1 2 3 4 5 6 7 8 9
2|2 4 6 8 1 1 1 1 1
3|3 6 9 1 1 1 2 2 2
4|4 8 1 1 2 2 2 3 3
5|5 1 1 2 2 3 3 4 4
6|6 1 1 2 3 3 4 4 5
7|7 1 2 2 3 4 4 5 6
8|8 1 2 3 4 4 5 6 7
9|9 1 2 3 4 5 6 7 8
これを見ると、1=18(22%),2=15(19%),3=11(14%),4=12(15%),5=6(7%),6=7(9%),7=4(5パーセント),8=5(6%),9=3(4%)となっていて、やはり1が多い。そして、全体としてベンフォードの法則に近いようである。
こう見ると、数はベンフォードの法則が成り立つようにできているのかもしれない。
2、二つの数目盛
前ページ【125、0と1】でやったように、数の構造を表わす図は二つある。一つは数直線目盛、もう一つは対数目盛である。
数直線目盛は加法についての目盛、対数目盛は乗法についての目盛となっている。
また、【79、ベンフォードの法則】では、自然数を集計しても最初の桁が1になる確率が多いことが示される。
1〜10000までの自然数で、最初の桁が1である割合と2である割合を調べると、次のグラフになる。

この図を見ると、相似形が浮かんでくる。
位が上がるたびに同じことがくりかえされているからだ。
そもそも、一桁目の数は1〜9までの数である。
だから、1の位にすると、x×10n(1≦x<10)と表わされるので、10nで相似形になることはすぐにわかる。
つまり、1〜10,10〜100.100〜1000,・・・と同じように数字が出てくる。
だから、これは対数目盛で表わせば同形になることに気がつく。
先のグラフを上のような対数目盛で作り直してみると、
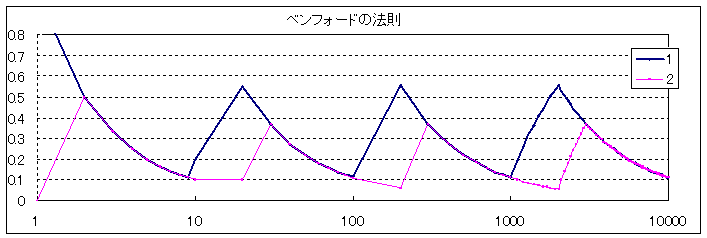
見事に相似形になる。
そうすると、当然1〜10に関しても相似形に縮小されているはずである。
そして、相似形だから割合も保存されている。
ちなみに、この曲線を積分すると1になる割合(確率)が求まる。
それは、24.1348%であった。
3、1〜10までの対数目盛
では、1〜10までの間はどのようになっているのだろうか。対数目盛は指数の大きさで長さを表わしたものであるから、指数間隔を等しく取っている。
1〜10までも同様にしてみると、
100 100.1 100.2 100.3 100.4 100.5 100.6 100.7 100.8 100.9 101
┷━━┷━━┷━━┷━━┷━━┷━━┷━━┷━━┷━━┷━━┷━
100.1=1.258925…
100.2=1.584893…(=(100.1)2)
100.3=1.995262…(=(100.1)3)
100.4=2.511886…
100.5=3.162277…
100.6=3.981071…
100.7=5.011872…
100.8=6.309573…
100.9=7.943282…
となっている。
これを見ると、不思議なことに1.…をとる数の幅が大きくなっている。
これは、x×10n(1≦x<10)のxの分布を示しているはずである。
それをもっと詳しく見ると(自然数で目盛ると)、次の目盛になる。
これを見ると、20,30,40,…の分布も全く同じようになっている。
これは、1の出る割合は、位が変わっても変わらないことを示している。
そうすると、1の出る割合はこの目盛の10に対する1の幅と同じになる。
数直線目盛では、横にずらしても1になる割合は変わらない。
これは加法に関して(nを加えても)1の割合が不変であることを示している。
4、n倍した時に分布はどうなるのか?
では、最初の九九の場合はどうなっているのだろうか。九九の表を10(指数)で表わしてみると、かけ算は指数の足し算になる。
(×) | 1 2 3 4 5 6 7 8 9
(+) | 0 0.301 0.477 0.602 0.699 0.778 0.845 0.903 0.954(指数)
1 0 | 0 0.301 0.477 0.602 0.699 0.778 0.845 0.903 0.954
2 0.301| 0.301 0.602 0.778 0.903 1 1.079 1.146 1.204 1.255
3 0.477| 0.477 0.778 0.954 1.079 1.176 1.255 1.322 1.380 1.431
4 0.602| 0.602 0.903 1.079 1.204 1.301 1.380 1.447 1.505 1.556
5 0.699| 0.699 1 1.176 1.301 1.398 1.477 1.544 1.602 1.653
6 0.778| 0.778 1.079 1.255 1.380 1.477 1.556 1.623 1.681 1.732
7 0.845| 0.845 1.146 1.322 1.447 1.544 1.623 1.690 1.748 1.799
8 0.903| 0.903 1.204 1.380 1.505 1.602 1.681 1.748 1.806 1.857
9 0.954| 0.954 1.255 1.431 1.556 1.653 1.732 1.799 1.857 1.908
(指数)
この場合、整数部は桁数、少数部が最初の数を表わしているので、小数部だけに注目すればよい。
指数の小数部0〜0.301が1にあたるが、これが多くなるのは当然である。
指数の加法は0〜1までの指数で均等(一様)になるはず。
指数について分布が均等(一様)になっているとすれば、1の出る割合はlog102=0.30103となる。
九九表がベンフォードの法則に近い理由がわかる。
これを積分で求めてみると、
1=24.1348
2=18.32
3=14.55
4=11.74
5= 9.50
6= 7.64
7= 6.05
8= 4.65
9= 3.42 であった。
九九表の1の割合が24%であるのは、1,2,3・・・を指数で表わすと、すでに偏っているからである。
さらに、対数目盛で乗法のしくみを調べてみると、
(この二つは同じ目盛で、1〜10までの目盛は23456789を示している。)
下の100=1を上の2にあわせるようにずらしたもので、下の数の2倍はそのすぐ上の数になっている。
5≦x<10の数は1*になることが一目でわかる。
これは、2倍しても、1になる数の幅が変わらない事を示している。
(水色の部分は1になる部分で幅は変わらない。)
同様に、3倍は、
となり、やはり100=1を上の3に合わすようにずらしただけで、3倍しても1になる幅は変わらない。
つまり、乗法に関しては横へずらすだけなので、k倍しても1の割合が変わらないことを示している。
5、指数関数はベンフォードの法則が成り立つ
ということは、指数が一様ならばベンフォードの法則が成り立つ。つまり、指数関数 y=ax はすべて指数が一様であり、ベンフォードの法則が成り立つ。
例えば、フィボナッチ数列は指数関数で表わされるので、ベンフォードの法則が成り立つ。
では、ベキ関数はどうだろうか?
まず、y=x2を調べてみよう。
nの出る割合は、(10(1/2・log(n+1))−10(1/2・logn))/(10(1/2・log10)−10(1/2・log1))
となり、y=xaでは、
(10(1/a・log(n+1))−10(1/a・logn))/(10(1/a・log10)−10(1/a・log1))
となる。
ということは、ベキ関数に関しては、上の公式で求めた割合になり、ベンフォードの法則は成り立たない。
つまり、指数関数については、1の出る割合はlog102=0.30103となり、
ベキ関数について1の出る割合は、xについて一様だと仮定すると、
a=2ならば、19%
a=3ならば、23%
a=−1ならば、55.5%
a=1ならば、11.1%
ところで、1の出る確率は0.241348であった。
2で求めたように、乗法で1が出る確率は24.1348%である。
この一致は、実数をかけあわせてできる数の世界での1の出る確率は、24.1348%ということを示している。
6、縮尺不変性について
普段見慣れている数直線目盛は、加法に関しては自然なのだが、乗法に関しては0に近い所がわかりにくい。乗法に関しては対数目盛の方が自然で、数の位を自然に表わしている。
この二つの目盛はともに実数を示す目盛であり、
加法をする場合は数直線目盛が、乗法をする場合は対数目盛がわかりやすい。
そして、この対数目盛はベンフォードの法則を示しており、
数(の集合)をk倍しても、最初の桁が1の割合は変わらないことを示している。
(ベキ関数の割合も)
「縮尺不変性」はもともと数の持っている(乗法の)性質なのだ。
このことは、対数目盛を調べている中で、少しずつ明らかになってきた。