人間の五感は対数に変換されている
･･･ウェーバー・フェヒナーの法則から平均律音階まで･･･
音は周波数という物理的な量を持っている。では、私たちがこの音を聞くときに、周波数に比例するように聞いているのだろうか。また、物を持ったとき、感覚だけで重さを当てることができるのだろうか。
そもそも、人間の感覚はあまり正確ではない。だから、感覚を正確にするために温度計や時計など様々なハカリが作られてきた。正確なハカリができると、今度は人間の感覚はどうなっているのかという先ほどの疑問が出てくる。そして、それをさぐるために様々な実験がなされ、いろいろな法則が発見されてきた。
でも、物理法則とは違い人間の感覚を正確に量化することは難しい。個人差もあれば、感じ方の曖昧さなどがあり、実験者のバイアスも入ってしまう。ここではそういう問題点を仮説に置き換えながら、数学的に考察してみようと思う。
１．ウェーバーの法則（1795年 - 1878年）ドイツの生理・心理学者が発見
『彼は、1834年に行なった錘を持ち上げる実験で、錘の重さの変化を感じ取る感覚は、何kg増えたかといった差ではなく、何倍になったかという比に依存しているということを示した。
《ウェーバーの法則》
「弁別閾（気づくことができる最小の刺激差）は、原刺激の値に比例している。」
ΔR(弁別閾)／R(刺激量) ＝ Ｋ(定数) (Ｋをウェーバー比という)･･･(1)
すなわち、100の刺激が110になったときはじめて「増加した」と気付くならば、200の刺激を増加したと気付かせるためには220にする必要がある（210では気付かない）。』 ―ウキペディアより―
T：２個の刺激強度を比較する場合、その差を感覚できる値域を弁別閾というが、この弁別閾がそのときの刺激強度に対する比は一定である。つまり、10g / 100g ＝ 20g / 200g ＝ 0.1＝Ｋ （実験値は1/40～1/30=0.033だが、計算をしやすくするための仮の値）という比例関係が存在するということ。
もっと具体的に言うと、
手に重りを100gのせ、そこに1gずつ重りを加える。その結果、重さを感じたのが110gの時。
手に重りを200gのせ、そこに1gずつ重りを加える。その結果、重さを感じたのが220gの時。
表にしてみよう。
刺激量：10 …100 200 300 400 … 1000
弁別閾： 1 … 10 20 30 40 … 100
S：すごい法則だね。刺激が大きくなってくると感覚は鈍くなるということか。
S：もしかしたらこの法則は、重さだけでなく、聴覚や視覚なんかにも当てはまるんではないの。
S：でも、これだけの結果から直ぐに全ての感覚がそうなっていると結論づけるのは間違いだよ。あくまで実験で確かめなくっちゃ。
T：そうですね。この法則から「人間の感覚は等差ではなく等比になっているのではないか」という仮説が生まれてきます。でも、それは後から確かめることにして、まず、この法則を定式化してみましょう。
S：等差ではなく等比になるということは、以前にやった貝の生長や人口やジップの法則、そして複利計算や経済の成長と同じということですね。
T：そうです。それをヒントに考えてみましょう。問題は感覚をどう定式化するかです。
S：(1)の式には感覚は出てきませんね。
S：最初の説明には、「錘の重さの変化を感じ取る感覚は、何kg増えたかといった差ではなく、何倍になったかという比に依存している」と書いてあるから感覚が数量化されたように思えるけど。
S：弁別閾と感覚がどう関係するかですね。
T：実は、ウェーバーの弟子でフェヒナーという人が同じように感覚量を問題としました。
２．フェヒナーの法則（1801年 - 1887年）
S：弁別閾＝感覚とするとおかしいけど、弁別閾を感覚の単位と考えたらどうかな。
T：すばらしい。フェヒナーの考えと同じだ。彼は、
「感覚量は直接測定できない。でも、弁別閾は人間の感覚の最小単位と考えられるのではないか。」
と考えました。
S：ということは、これは仮説ですね。（フェヒナーの仮説）
S：弁別閾を基本の単位として間接的に感覚量を尺度化したわけですね。
刺激量 100-110 200-220 300-330 400-440 …
弁別閾 10 20 30 40
感覚単位 +1 +1 +1 +1
S：そうすると、二つの刺激の間の感覚の違いをどう表すのかということになりますね。
T：そうです。例えば、刺激は連続的に変化しているわけだから、弁別閾も連続的に変化しています。それを表にしてみましょう。
弁別閾は刺激の10％ずつ増えていくわけだから、刺激の増加は次のような表になります。このとき増分が弁別閾ですが、仮説の通りこの増分を感覚の単位とすれば、（ここでは仮に刺激量100の時の感覚量を１とする）弁別閾を刺激量にプラスすれば感覚量は１増えるはずです。
×1.1 ×1.1 ×1.1 … +ΔR
刺激量 100 110 121 133 146 160 176 193 212 233
弁別閾 +10 +11 +12.1 +13.3 +14.6 +16 +17.6 +19.3 +21.2
感覚量 1 2 3 4 5 6 7 8 9 10
+ΔE
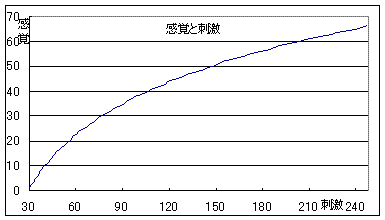
S：これだったら感覚量Eと刺激量Rの関係を式にできますね。
S：刺激量＝100×1.1^（感覚量－１）･･･(2)
と表すことができます。
S：指数関数になるんですね。
S：でも、感覚量を求めるにはどうしたらいいのですか？
T：指数関数の逆関数を使えばいいのですよ。
S：x = apのとき、p = loga x だから、
感覚量－１＝log1.1（刺激量／100）
（100は、本来は最小刺激量）
E＝log1.1（R/100）＋1 ･･･(3)
（右のグラフは、E＝log1.033(R/30)+1 ）
S：対数関数になりました。
S：ということは、感覚量は刺激量の対数で求まるということですか？
T：そうです。フェヒナーは微分方程式を解いて求めています。一応紹介しておきます。
『刺激量を増やしたときに、感覚の大きさの微少な増分dEと微少な刺激増分dRとの間に、上の表からわかるように、dE/dRは刺激量Rに反比例するという関係が出てきます。つまり、
dE/dR＝10/R
dE＝10･dR/R
と表せます。この両辺を積分すると、（感覚増分を積算すると感覚量が求まる）
∫dE＝∫10･dR/R （∫は積分記号）
E＝10･∫(1/R)dR (loge x)'＝1/x だから、
＝10･logR+C ･･･(4)（C:積分定数，logは自然対数） 』
となります。この式は、感覚の大きさEは，刺激強度の対数に比例することを意味しています。
これがフェヒナーの法則です。
S：最初の感覚の大きさの増分を考えた所が、弁別閾の増分からきているわけですね。
S：ところで、(3)の式と(4)の式は違いますが、どうしてなんですか？
T：気がつきましたか。実は、先ほどの表は連続になっていないのです。100→110となっていて、折れ線です。101→110.1も増えているので、それらを加算する必要があります。それを考慮して刺激量の増加を無限回組み込んだとすると、(2)式は、
刺激量＝100×e0.1(感覚量－1) となる。
よって、
E＝1／0.1×loge(R/100)+1
E＝10×loge(R/100)+1 となって、(4)とほぼ同じになる。
《フェヒナーの法則》
「感覚量は刺激強度の対数に比例する。」
E(感覚量<心理量>) ＝ｋ(定数)log R(刺激強度)
T：さて、これは他の感覚にも当てはまっているのでしょうか。初めに音について調べてみましょう。
３．音はどう聞こえるか
○音量とデシベル
T：音量はデシベル(ｄＢ)で表されています。１Ｂ(ベル)＝１０ｄＢで、電話を発明したベルさんからとっている。
120dB ジェット機の騒音
110dB 自動車の警笛
100dB 電車が通るときのガード下
90dB 大声による独唱、騒々しい工場の中
80dB 地下鉄の車内、電車の中
70dB 電話のベル・騒々しい街頭、騒々しい事務所の中
60dB 静かな乗用車、普通の会話
50dB 静かな事務所
40dB 図書館や静かな住宅地の昼間、コオロギの鳴き声
30dB 郊外の深夜、ささやき声
20dB 木の葉のふれ合う音、置時計の秒針の音
10dB 蝶の羽ばたき
『音量は物理的には、アンプで言うと電力（Ｗ）などで表されます。経験的に、スピーカーの出力が１Ｗから２Ｗへ「１Ｗだけ」大きくなった時、人間の耳には音が大きくなったと感じることができます。しかし１０Ｗから１１Ｗへ「１Ｗだけ」大きくなった時には音の変化を感じとることが難しい。つまり１Ｗから２Ｗの変化は「２倍」ですが１０Ｗから１１Ｗの変化は「１.１倍」となり、人間は音の出力の差ではなく比で音の大きさを感じとり、人間の感覚と音の大きさは等比関係ではなく対数関係になっています。』
電圧量 1 - 2 10 - 11 10 - 20 (W)
弁別閾 1 1 10 (W)
S：「比で音の大きさを感じ取っている」ということは、弁別閾が物理的な音量と一定の比を持っているということだから、ウェーバー・フェヒナーの法則が使えますね。
S：でも、音量の単位デシベルは、ある意味で物理量だから心理量とは違いますね。結局、ウェーバー・フェヒナーの法則を使ってデシベルを決めたということですね。
T：そうなんだ。本当に感覚がそうなっているのか実験データを調べたが、サイトには出ていなかった。
S：ということは、音の大きさの物理量と感覚量の間の関係がウェーバー・フェヒナーの法則にしたがっていると仮定して調べていけばいいわけですね。
T：そうだね。まず、デシベルの定義を見てみよう。
『音量のデシベルの定義
ｄＢは 基準値と比較して何倍、或いは何分の１であるかという事を対数（log）を用いて表現するための単位記号で、これを使って大きさや量を表すには基準になる大きさや量が必要です。
基準となる音圧は通常の人の耳に聞こえる最小音圧の２×１０-5Ｎ／㎡（＝Pa）と比較してどの程度大きいかという表現です。
音量（ｄＢ）＝１０･ｌｏｇ（対象の音圧／最小基本音圧）2
最小音圧＝0.00002Ｐa 』
T：音圧というのは、音が伝わるときには、圧力の高い部分と低い部分ができるだろう。この圧力の変化量を“音圧”っていうんだ。単位はパスカル（Ｐａ）。（音圧と電力は同じと考えてよい）
S：この最小音圧って聞き取れる最小の音圧ですね。これが、さっきの弁別閾にあたるんですね。
S：１０倍は、ベルをデシベルに直すためだということはわかるけど、なぜ２乗しているのですか？
T：デシベルは元々オーディオ機器（アンプなど）で使われているから、電気に関わって定義された。ワットは電力=電圧×電流 だから、電流と電圧それぞれで定義されているとしたら、ワットは２乗しなければ都合が悪くなる。
とりあえず、これを表にしてみよう。
(最小音圧) ×10 ×10 ×10 ×10 ×10 ×10（最大音圧）（106)
音圧 0.00002 0.0002 0.002 0.02 0.2 2 20Ｐa
音量 0 20 40 60 80 100 120ｄB
E 0 1 2 3 4 5 6
S：音圧という物理量は1000000倍にわたっているけど、それを桁数だけにすればはるかに小さい範囲（0～120ｄB）で表すことができるということですね。
S：しかも、感覚とよくあっている。
T：ただし、振動数が同じ音の場合だけしか成り立たないようだよ。
S：さっき物理的な音量をワットで考えたけど、音圧はワットに直せるの？
T：その音を出力に換算すると、なんと10-10W（10のマイナス12乗ワット＝ 0.000000000001 ワット）という極少の値になるそうです。
S：最小音圧がわかっていればこれを最小の弁別閾と仮定して式を求めることができるわけだ。
S：でもそれなら、弁別閾は音圧によって変化するわけだから、それぞれの音圧によって最小音圧も変わるはず。どうして割るんだろう？
T：上の表から、
音圧R＝0.00002×10E となっています。逆関数を求めると、
E＝log10(R/0.00002) となります。
一方、デシベルはベルの10倍であり、２乗なので２倍になります。
つまり、音量＝10×2×E
S：聞き分けられる最小の音の音量は０ｄBで、弁別閾は１０倍ずつ増えていると仮定して式を作っているんですね。
○音の周波数･･･周波数と音階
T：今度は周波数だよ。人間は２０～２０００ヘルツ程度の音を聞くことが出来ると言われている。
S：１０００倍か。音量よりは少ないけど、巾は大きいね。
S：周波数は物理量だけれど音階になるのだから、感覚といってもけっこう正確に求められるんじゃないのかな。
T：それが、絶対音感のある人以外はけっこう曖昧なんだ。さて、ここにも対数が出てくるのでしょうか。･･･
音は鼓膜で振動し、それが蝸牛管で電流に変換される。このときの変換が等差だとすれば、受け取るほうの脳の目盛はたくさん必要になります。それに、音程は倍音ですよね。
S：やっぱり等比で分けないと脳が大変なんだ。
T：仮に、20～2000までの周波数を等比で分けてみましょう。1000倍を２倍ずつに分けると、ちょうど２10＝１０２４でほぼ10等分できます。
S：なぜ２倍になるように分けるのですか？
S：「２倍の倍音は同じ音程に聞こえる」ということはピタゴラスが発見したんですよね。音程にとって２倍音は大事なんだ。
（参考 【89.音階を作ってみよう】へ）
S：ついでに、ﾄﾞと高いﾄﾞの周波数にあわせるように数値を取ると、
×2 ×2 ×2 ×2 ×2 ×2 ×2 ×2 ×2 ×2 ･
周波数 16 32 65 130 261 523 1046 2092 4184 8369 16735
弁別閾 +16 +32 +64 +131 +262 +523
対数変換 １ ２ ３ ４ ５ ６ ７ ８ ９ １０ １１
音階 ド ド ド ド ド
S：ちょうど１０オクターブに分けることができた。
S：人間の耳はもっと細かく聞き分けれれるから、５と６の間をもっと分割してみよう。
T：1オクターブは８だけど、ピアノは半音を入れて１２の鍵盤があるから１２等分をしてみよう。もちろん等差ではなく等比になるように分けなければいけない。（等比に等分することの意味→【78.比例を拡げる】へ）
S：２６２Hｚから５２３Hｚを１２分割するには、２倍をさらに細かくすればいいんですね。
S：等比級数で書くと、1=20/12，21/12，22/12，23/12，…，212/12=2 となるはず。21/12≒20.083≒1.06 だから、（1.0612＝2.0121）
×1.06×1.06×1.06×1.06×1.06×1.06×1.06×1.06×1.06×1.06・・
周波数 262 277 294 311 330 349 370 392 415 440 466 494 523
音階 ド ド# レ レ# ミ ファ ファ# ソ ソ# ラ ラ# シ ド
弁別閾 15.7 16.6 17.6 18.7 19 21 22 23 25 26 28 29
対数 5 5.08 5.17 5.25 5.33 5.41 5.49 5.58 5.67 5.75 5.83 5.92 6.00
+0.083 +0.083 +0.083 …
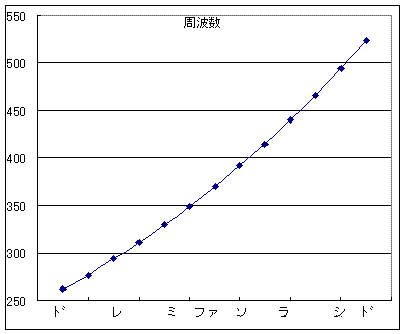S：つまり音階も対数変換ととらえることができる。log2(周波数)＝音階といっても良いね。
S：以前ピタゴラス音階を調べたけど、これは少し違いますね。
T：これは、１２平均律といって、ピアノなどに用いられている音階です。
S：どう違うのですか？
T：これは、移調が簡単。レをドと考えて同じように音階をふっていけば、ドレミができてしまう。ピタゴラス音階とあっている音程もあるんですよ。
S：６％ずつの成長率と同じですね。
参考文献 畑村洋太郎著「数に強くなる」岩波新書
４．「人の感覚と対数」
T：さて、これまでのことから、人間の感覚は対数に変換されているという仮説が出てくる。
S：でも、感覚量は正確に計れないし、今まで見てきたようにウェーバー・フェヒナーの法則を既定のものとして当てはめている所があるような気がするな。
T：ここで、以前考えたお金の価値について、感覚量の考え（フェヒナーの仮説）から調べてみよう。
○お金の価値は対数変換されている
T：フェヒナーの仮説をお金に当てはめてみると、「お金の感覚価値は全体に対する割合から決定する」といえる。
S：全体というのは何に対して？
S：その人が所有している財産とみなしていいのじゃないかな。
S：刺激量を財産、弁別閾を使う金額とみなすわけですね。
T：その比が常に同じと仮定するわけです。そうすると、同じ議論ができ、「お金の価値は所有している財産によって決定する。」つまり、お金の心理的な価値は財産の対数となるということがいえる。
R 財産 100 200 300 万円
ΔR 金額 1 2 3 万円
E 価値 2log1 2log2 2log3
S：お金に関しても対数的なのは、等比だということからわかるね。
T：利息とは、そのお金が生み出す値打ち。そして、「利息は全体の同じ割合から求まる」ということが仮説になっている。割合が同じ限り等比なのだから、これまで考察したように、感覚は対数変換できる。
しかし、この仮説が本当に正しいのかは考えてみなければいけない。等比的ではなく「累進課税」みたいな考え方だってある。利息が元本の割合として表される限り、財産が指数的に増えていくのは当然だよ。
S：1000円を持っている時に100円使うのはキツイけれど、10000円なら余裕だと感じるということか。
S：逆に、利息を累減させれば、もっと平等になるということですね。
T：ここで、利率を弁別閾と考えてみよう。例えば、年間１０％ずつの複利計算は、元本＝10×1.1(時間－1) で表される。
×1.1 ×1.1 ･･･ ×10 ×10
元本： 10 11 12 13.3 … 100 1000 10000 円
利息： 1 1.1 1.21 1.331 10 100 1000 円
時間： 1 2 3 4 25.2 49.9 73.5 年
心理金額： 10 20 30 40 252 499 735 心円
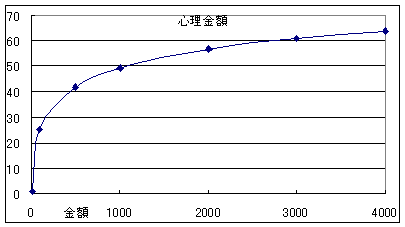表はこのようになります。
S：重さの時にやったのと同じだね。E＝24.15･log10(R/10)+1 だ。
S：利息が弁別閾だ。
S：ここでは、元本に対して時間が対数になっているわけか。ということは時間＝心理金額と考えることができる。
S：11円が20心円とはどういうこと？
S：10円が11円になるのに1年かかるから、2倍の20円と考えたらどう。
S：1000円から逆に安くなっていますね。
S：金額が増えると指数関数で利息が増えていくので、年数が少なくなるからだよ。
T：今度は利息の値を代えてみよう。今は利息が0.3％ぐらいだから、E＝(1/log101.003)･log10(R/10)+1
元本 1万 10万 100万 1000万 1億 10億 100億 1000億 1兆 10兆 円
利息 30 300 300 3000 3万 30万 300万 3000万 3億 30億 円
心理金額 1 770 1538 2307 3075 3844 4613 5381 6150 6919 心円
S：１万から１０万円を作るには770年かかるので心理的には770万円と感じる。1兆円は感覚的には6150万円ぐらいにしか感じない。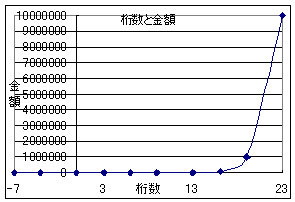
S：心理的金額は、１万円を基準にしたのですね。なんとなくわかるような。
S：まさに、Time is money. ですね。
S：右のグラフは、利息が同じ割合でつく限り金持ちはますます金持ちになるということか。
【あなたの金持ち度「Global Rich List」】
S：これが金持ちに関するベキ法則が成り立つ一番の原因じゃないの。
【65.「ベキ関数」から「スモールワールド」へ】
T：ただ、私たちはお金に関しては無意識のうちに対数変換しているから、逆に気をつけなくてはいけないところがある。
【67.私たちは、お金を対数目盛で考えている！？】
○地震のマグニチュードは、なぜ対数目盛になっているのか
『マグニチュード（magnitude）とは、地震が発するエネルギーの大きさを表した指標値である。1935年に、アメリカの地震学者チャールズ・リヒターによって初めて定義された。マグニチュードはエネルギーの対数をとったもので、マグニチュードが2増えるとエネルギーは1000倍になる。
リヒターは、ウッド・アンダーソン型地震計（2800倍）の最大振幅A（単位：μm）を震央からの距離100kmのところに値に換算したものの常用対数をマグニチュードとした。従って、地震波の振幅が10倍大きくなるごとに、マグニチュードが1ずつあがる。
ML = log10A 』
S：この定義はわかりやすいですね。底が１０だから桁数だけを見れば直ぐに変換できますね。
T：でも、最近ではもっと複雑な式が使われている。
『地震が発するエネルギーの大きさをE（単位：J（ジュール））、マグニチュードをMとすると
log10E = 4.8 + 1.5M
という関係がある（マグニチュードの計算に用いる対数は常用対数である）。このことと一般的な波動の性質から、マグニチュードが1増えるとエネルギーは１０√１０倍（およそ31.62倍）になる。』
S：なぜ4.8を足すのか、1.5倍するのかわかりません。
T：説明すると余計わからなくなるからやめよう。
S：さっきの「マグニチュードが2増えるとエネルギーは1000倍になる」というのは、間違いではないですか。だって、桁数が2増えるとエネルギーは100倍でしょう。
T：いや、これは、log10E0 = 4.8 + 1.5M の定義に当てはめると、
logE0=4.8+1.5M
logE1=4.8+1.5(M+1)
logE1=4.8+1.5M+1.5
logE1-logE0=1.5
log(E1/E0)=1.5
E1/E0=101.5=10(3/2)=√103=10√10
+1で10√10なので、+2だと、10√10×10√10=1000 となる。
『Ｍの平易かつ効果的な説明法としては「地震は地下の（震源）断層面の破壊で生じる．Ｍは，その断層面積の目安である」と説明し，「Ｍ６でだいたい10km，Ｍ７で30km，Ｍ８で100kmにわたって広がる断層面が破壊し，そこから地震波が発生する」と付け加えれば，エネルギーの概念を解さない人を含む多くの市民に，Ｍの防災上の意味が理解可能と思われる．』
S：もっとわかりませんよ。
T：とにかく最初の定義は、エネルギーの対数だったということで良いことにしよう。
○《星の明るさも対数表示》
T：星の明るさを「１等星」「２等星」などと呼ぶのを知っていますね。この数字は、目が星から受ける光の強さの対数になっています。
S：光度は確かルックスですよね。そのルックスの対数をとるということですか。
『等級が1等級変わると明るさは100の5乗根、すなわち約2.512倍変化する。よって等級差が5等級の場合に明るさの差が正確に100倍となる。』
S：つまり、6等級を１とすれば、
×2.512 ×2.512 ×2.512 ×2.512
光度：1000 1001/5 1002/5 1003/5 1004/5 100 1006/5 1007/5
1 2.512 6.31 15.851 39.81 100 251.2 631.01
等級： ６ ５ ４ ３ ２ １ ０ －１
S：なぜ１００の5乗根倍なんですか。
T：最初に１から６等級までを決めたからだろう。一番明るい星を１、一番くらい星を６としてその間を等比に６等分したわけですね。そして、19世紀の天文学者ポグソンは、実際に明るさを定量的に測定し、1等星と6等星は明るさの差がおよそ100倍であることを見つけた。そして、等級が5等級変化するごとに明るさが100倍になる、すなわち1等級が1001/5 ≒ 2.512倍に相当すると定義したのです。
S：人間が見える明るさは、ウェーバー・フェヒナーの法則に当てはまっていると仮定して決めたんですね。
S：これだとマイナス等星だけでなく、少数等星も決めることができますね。
○《ジャネの法則》 感覚年齢も対数
T：以前、「年齢と感覚時間は反比例する」ということを話したね。これは、感覚時間／年齢＝一定ということで、この場合の感覚時間は弁別閾でありこれまでの議論が適用できる。
S：感覚年齢を求めることができるということですね。
T：まず、次の仮説を設定する。
「感覚年齢τの増加（=感覚時間Δτ）は、自分の知識（=記憶）の総量が何パーセント増加したかという割合に比例する。つまり、Δτ＝知識の増量／知識の総量。」
S：（知識の増量）÷（時間の増量）＝（知識の時間に対する増加率）だけど、（知識の増量）÷（知識の総量）＝（知識の全体に対する増加率）といってもいいのか。ということは、（知識の全体に対する増加率）＝（感覚時間）は（知識の総量）に反比例している。
S：知識の総量でなく、起きている時間の総量では駄目なの？
T：実はいろいろな定義があるけど結果は同じ。なんといっても心理時間だから経験＝知識の量と考えても良いでしょう。どんどん進めるよ。
「知識（記憶）の総量はその人の生きた物理的時間t、つまり年齢に比例する」と仮定しよう。
S：なんだ。起きている時間に戻ったよ。つまり、知識の増量も時間の増量に比例する。
S：Δτ＝時間の増量／年齢となり、年齢と弁別閾（Δτ）が反比例しているわけですね。
S：しかも、この場合は感覚時間の総和が感覚年齢になるから簡単に求まるね。
年齢 0 1 2 3 4 5 ･･･
感覚時間 1 1/2 1/3 1/4 1/5 ･･･
感覚年齢 0 1 1+1/2 1+1/2+1/3 1+1/2+1/3+1/4 1+1/2+1/3+1/4+1/5
T：これは一年間隔だから、もっと細かく区切ると値が違ってくる。とりあえず、ウェーバー・フェヒナーの法則に当てはめてみよう。
ΔτはΔt／t に比例することになり、
Δτ＝ｋΔt／t
Δτ＝ｋ（1／ｔ）Δt ･･･ 両辺を積分すると
∫Δτ＝∫ｋ（1／ｔ）Δt
τ＝ｋ･loge ｔ＋C （0歳のときにτ＝0になるようにCをとる）
S：フェヒナーの計算と全く同じですね。
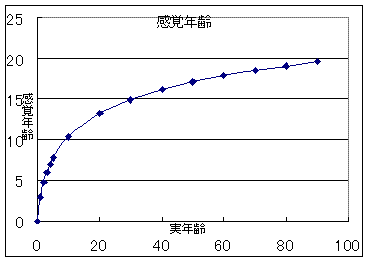
S：グラフを見ると、齢を重ねるにしたがって、増加率が非常に緩慢になっている。
S：Δτは感覚時間で、τは感覚年齢ということか。「感覚年齢は実際の年齢の対数となる」ですね。
T：ｋをどういう値にとれば一番合うのか迷ったけど、とりあえず１０歳にあわせてみた。
S：このグラフを見ると、80歳の人の感覚年数の半分（折り返し点）は８歳ぐらいですね。
S：感覚時間については調べた人はいるのですか？
T：ちゃんといるんです。その人の名前をとって、「ジャネの法則」と言います。
『１９世紀のフランスの哲学者・ポール・ジャネが発案し、甥の心理学者・ピエール・ジャネが著作で紹介した法則のことである。簡単に言えば生涯のある時期における時間の心理的長さは年齢の逆数に比例し、年齢に反比例する。
例えば、50歳の人間にとって1年の長さは人生の50分の1ほどであるが5歳の人間にとっては5分の1に相当する。よって、50歳の人間にとっての10年間は5歳の人間にとっての1年間である。1歳の人の1日が50歳の人の50日にあたることになる。』
S：へー。どうやって調べたんだろう？
T：感覚時間の弁別閾を実際の時間と比べたんだろう。君たちもよくストップウオッチでやっているじゃない。
S：でも、赤ちゃんは測れないでしょう。
あとがき
ここでは、感覚（心理）量というものを、いろいろな仮説を用いて考察してきた。感覚（心理）量は、重さ、音、お金、明るさ、時間、味、寒暖、匂いなどいろいろ考えられる。その時に問題となるのはやはり私たちの脳であろう。
生物は幅広い範囲の刺激をとらえられないと生存できない。しかし、刺激の全ての範囲を入力し処理しようとすると、脳には膨大な作業負担がかかる。そこで、対数変換をするように進化してきたのが私たち人間なのではないだろうか。
○面白サイトの紹介
「音は脳がつくりだしている」ということを実験できる。→リンク【錯視と空耳のアナロジー】のページへ
目次へもどる