音階を作ってみよう！
１、糸電話からモノコードへ
T：紙コップで糸電話を作ったよ。話してみよう。
S：小さな声で話してもはっきり聞こえる。
T：（糸電話で話しかけながら）こんなに小さな声で話しても聞こえるのはなぜ？
S：糸が震えているから、ふるえ（振動）が伝わる。
T：振動が伝わっているんだね。声帯から出た振動は空気を揺らしてコップの底を揺らして…？
S：糸を振動させてまたコップの底を振動させる。さらに空気を振動させ、鼓膜を振動させる。
T：そして骨を振動させ、今度は電気の振動となって脳に伝わる。
S：高い音と低い音は振動がどう違うの？
T：調べてみようか。（私の流儀はとにかく実際にやってみる。）先ずこの紙コップを使ってモノコードを作ってみよう。（右の写真→）
（必要なものは、木の板・釣り糸・コップ・画鋲・輪ゴム）輪ゴムは弦を引っ張るときに使う。
（インスタントラーメンのコップをつけてみた。コップを逆につけたら弦を短くできる。→）
S：弦の長さを決めるためには爪がいるね。
S：紙で作れば簡単だよ。
S：これって、ギターみたいですね。短くすると音が高くなるよ。振動が速くなるんだ。
T：ピタゴラスは音楽の理論を研究するときにモノコードを使って調べたんだよ。
S：これを使ってピタゴラスの足跡をたどってみようということですね。
２、モノコードで音階を作ってみよう
T：音階は、どうやって決めればいいのだろう？
「音階を作るには、はかりの作り方を思い出してください。
はかり（重さや長さの認識）は、[直接比較]→[間接比較]→[個別単位]→[自分のはかり]→[普遍単位]→[半端な量の測定]、へと発展していきます。長さ、重さ、面積、体積等はほぼこの道筋を通って認識が深まっていきます。音階も同様にして認識が深まります。もちろんそこには人間の感覚のあいまいさが前提になっていますが、はかり作りと同様に音階作りが認識を深めるポイントです。」
S：どこかをドにすればいいんでしょう。
S：どうやってドを決めたの？
S：周波数でドを定義してるんでしょう。でも、当時はそもそもドがないんだから適当に決めたんじゃない。
S：じゃあ、ここをとりあえずドにしてみよう。
T：次はどんな音階が決まる？
S：ドの長さの半分はどう？高くなるよ。
S：結構高い音だな。ソかな。
S：違うよ。高いドだよ。１オクターブ高くなるんだ。
「７音なのにオクターブ（８音階）というのは、ヨーロッパの数え方によります。ヨーロッパでは、ﾄﾞを１として高いﾄﾞまで８音階と数えますが、インド音楽ではドを０として７音階と数えセプターブと言うそうです。また、日本では古来５音階や７音階でした。８音階は絶対的なものではありません。」
T：音階も比べたいね。モノコードでは２つの音が比べられないから、弦を２つにしようか。これは、モノコードじゃなくて、ジコードだね。
S：ドと高いﾄﾞを一緒に弾くと…、何となく合っているような気がするな。
S：他の所と比べるときれいな音になると思うけど。
S：そうかな。音階ってけっこう思い込みかもしれない。
T：今まで聞きなれていることもあるかもしれないね。さて、全くドレミを知らないとして音階を作るにはどうしたらいいのだろう？
S：この半分を７等分したらどうかな。
S：でも、僕はギターをやっているけど、フラットの間は長さが違うよ。それに１２音あるし。
S：音を聞いて適当な長さを決めるのかな。
T：実は、この音階の決め方は全く数学的なんだ。ピタゴラスが比を大事にしたという話は知っているね。彼は、音階も比で求めようとしたんだ。まず、高いドは１：２。次に考えられる比は何だろう？
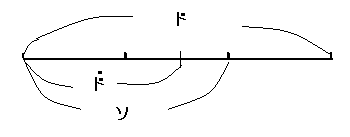S：１：３ではもっと高くなるから、１：２以上だと、２：３が次に簡単な比です。
T：では、２：３の所に印をつけて音を出してみよう。これは何の音？
S：ソだね。でも、どうして長さの比を選んだんだろう。
S：このソの音はドとよく合うからじゃないかな。
S：ドとソは和音だもんね。
T：このﾄﾞからソへの高さを完全５度と言います。では、次の音は？
S：次に簡単な比は４：３。いや、５：３かな？
S：ソの音から２：３で新しい音をつくる方法もあるよ。
T：どちらの方法も新しい音を作ることができます。整数比だと弦が共鳴しやすいんだろうね。ピタゴラスは、２：３を次から次へと当てはめる方法を採用しました。ここでは、この方法でやってみましょう。
「単純な比だけで音階を作る方法を、純正律音階といい、各音が最も調和しています。しかし、現代（のピアノなどの調律）はピタゴラス音階も純正律音階も使わないで、平均律音階を使っています。」
S：ソを２：３に分けるということは、ソの２／３だから、ﾄﾞから言うと４／９になるよ。これだと、高いﾄﾞを越えてしまう。
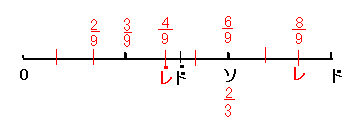T：そうなんだ。そこで、今度は１オクターブ下げる。計算で言うと、２倍するんだ。
S：８／９ですね。これはレですね。
S：次も、２：３に分けると、(８／９)×(２／３)＝１６／２７。これは･･･ラかな？
S：同様に、(１６／２７)×(２／３)＝３２／８１だから、さらに２倍すると、６４／８１。これはミだ。
S：どんどんできるね。次は(６４／８１)×(２／３)＝１２８／２４３。これはシかな。
S：後は、ファだね。(１２８／２４３)×(２／３)×２＝５１２／７２９＝0.7023319
S：このファを(２／３)するとﾄﾞになるのかな。でも、これって絶対に約分できないからどんどん複雑な分数になりますね。
T：いや、ファだけは高いドを３／２倍するんだ。つまり、（１／２）×（３／２）＝３／４とやって作る。
S：３／４＝０.７５だから、さっきの出し方の値とは違いますね。でも、これで、８音階ができたことになりますね。（ファの作り方の違いは、７章で分かります。）
３、音階とピタゴラス
S：ところで、なぜオクターブは８なの？
S：そうだよね。８音階はどうやって決めたの
T：頭の中でドレミファソラシドと言ってごらん。どれだけ高くしていっても音程は変わらないんじゃない？
S：ホントだ。音階というのは繰返すということか。音は繰返すということを発見したんだね。音楽で音階とは言葉みたいなものなんだ。
S：ぼくは、音楽が苦手だから音階もわからない。
T：そこで例によって、実際に作りながら、試しながら少しずつ理解していこう。１オクターブを８音階に分けたのがピタゴラスだ。そして、音楽も数学の原理にかなっていると主張した。音と音の周波数比ができるだけ小さな整数の比になっているという考えは、後に波動理論にもつながっていく。ピタゴラスは「数は万物のもとである」と考えていたから、音階も整数比でできていると考えたんだろうね。
４、「オクトパス」と「オクトーバー」と「オクターブ」
S：オクトパスって蛸（たこ）でしょう。蛸は８本の足があるから、オクトは８という意味なんだ。
S：オクターブも８音階ということでしょう。
S：でも、オクトーバーは１０月だよ。
T：本当は８月だったのですよ。
S：どうして８月が１０月になったの？
T：ローマ帝国初代皇帝アウグストスが変えたんだよ。それまでは、Actoberは８月だった。義理の父であるジュリアス・シーザーの誕生した７月をJulius（ジュライ）、自分の誕生した８月をAugustus（オウガスト）と変えたので、２か月分ずれることになってしまったらしい。
S：Septemberは７月で、Novemberは９月。Ｄecemberは１０月だったのか。
S：デカメロンは１０日物語だもんね。
T：それ以後の皇帝も誕生月に自分の名前をつけたが、その皇帝の死後はまた元にもどったらしい。
S：ネロの月なんていやだよ。
５、三分損益法
S：古代中国では音階はどうやって作られていたの？
T：中国の場合は弦ではなく、竹管を使って音階が作られていた。これも実際にやってみよう。節つきの女竹を用意してください。この竹を切り、切り口に唇を当てて吹くと音が出ます。
S：ビール瓶も音が出ますね。
T：唇の当て方や角度さえわかればいい音が出ます。でも、節がないと音は出ません。
S：竹と弦ではどう違うのかな？
S：弦は糸が振動する。竹は空気が振動する。でも、空気はどうやって振動しているのだろう。
T：竹の中に音が入ると、色々な雑音が出る。そのうち竹管の中に定常波ができる振動数の波だけが生き残るんだ。これを気柱共鳴といい、竹管の長さによって音程も違ってくる。
S：空気の振動って縦波でしょう。それがどうやって定常波になるのかな？
「振動は長さによって異なってきます。また、長さが一緒なら共鳴します。これは、波の特徴で、ここでは振り子も波の一種と考えて、共鳴することを動画で示します。竹管の場合、色々な音が出る中で、竹の長さの音だけが共鳴して聞こえてくるのでしょう。」
【動画：振り子の共鳴】
T：まず「三分損一」について説明するよ。長さ９寸の竹管から出る音を壱越(いちこつ)と決め、９寸を３分して、その３分の１を捨てると６寸になる。
この６寸の竹管から出る音が９寸の壱越に最もよく調和する。これを黄鐘(おうじき)と名づける。
S：３分してその１／３を捨てるから三分損一と言うのか。
S：計算で言うと、長さに２／３をかけることになるね。
S：これは、ピタゴラスと同じだね。弦か管の違いだけだ。
T：次は「三分益一」だ。６寸の竹管から最も調和する音を見いだすために、６寸を３分してその１／３を益すと８寸になる。
S：つまり、「三分損一」は長さで言うと２／３を求め、「三分益一」は４／３を出すことになるわけか。
「ちなみに、竹管は長さで音程が決まり、太さには因りません。この三本の竹管は皆同じ音が出ます。それに対して、弦の場合は、糸の長さだけではなく、張る強さ、糸の太さなど色々な要因が絡んできます。」
T：これを交互に繰返します。そうすると、やがて壱越の１／２になる所があります。
S：計算してみよう。(２／３)×(４／３)^6＝262144／531441＝0.4932701≒0.5
S：ぴったり0.5にはなりませんね。それから、音は１２音できることになります。
T：日本ではこれを順八逆六法という。
S：１２音全部使っていたんですか？
T：いや、５音から７音を使います。例えば、ドレミで表すとドレミ♭ソソラ♭ドドとなります。
T：音階を正確に聞き分けるソフトがあります。これも使いましょう。【おんかい君】です。このフリーソフトは、マイクをつけて、声を出すと、その音程が何かを示してくれます。
S：パイプを使うと音程がはっきりとわかりますね。この竹の長さを切っていけばぴったりと音程を合わせることもできますね。
S：でも、さっきのモノコードは瞬間の音なので、はっきりとはわかりませんね。
T：そうなんです。弦はあまり揺れないのです。笛は息が続く限り音が出ていますからこのソフトを使うにはばっちり。このソフトを使って確かめながら削って作ったのがこのサンポーニャです。フォルクローレは乾いた音がぴったり。【動画で音を聞いてみよう】
S：ところで、三分損益法はピタゴラス音階の作り方と同じように思えるのですが、違いはあるのですか？
T：比較表を作ってみましょう。ちなみに整数比だけで作る純正律の音階も入れてみました。三分損益はレ（壱越）が基準ですから、それをドに直したのが古代中国の音階です。なお、長さは周波数に反比例しますから、ここでは笛の長さの逆数にしました。
ピタゴラス音階 純正律音階 平均律音階 古代中国音階←三分損益法 *
ﾄﾞ １ １ １ １ ８／９ *
レ ９／８ ９／８ ２^(2/12) 1.125 １
1.125 1.125 1.12246 １ *
ミ 81／64 ５／４ ２^(4/12) 1.265625 9/8
1.265625 1.25 1.259921 1.125 *
ファ ４／３ ４／３ ２^(5/12) 1.3515243 19683／8192
1.3333 1.3333 1.33484 1.2013549 *
ソ ３／２ ３／２ ２^(7/12) 1.5206042 177147／65530
1.5 1.5 1.498307 1.3516481 *
ラ 27／16 ５／３ ２^(9/12) 1.6875001 ３／２
1.6875 1.666… 1.681793 1.5 *
シ 243／128 15／8 ２^(11/12) 1.8984376 ２７／１６
1.8984375 1.875 1.887749 1.6875 *
ﾄﾞ ２ ２ ２^(12/12) 2.0272866 59049／32768
2 1.8020324 *
レ 531441／262120
2.0274721 *
S：半音って何？
S：ミとファの間にどうして黒い鍵盤がないの？
S：和音はどうしてハモルの？
T：これらの質問には今までのことを使って、ある程度説明できるはずだよね。考えてみてください。最後に、数学的にまとめてみよう。以前やった分数多角形を使って説明するよ。
７、正７／３角形と正１２／５角形と音階
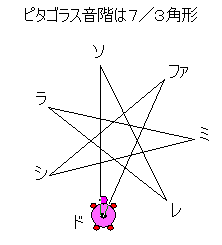
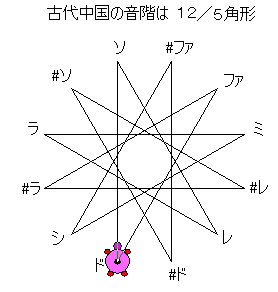T：これはピタゴラス音階の作り方が７／３角形で、三分損益の音階の作り方が１２／５角形になっています。ピタゴラスの方は、ファはﾄﾞの方から作るから完全な７／３角形になるわけではありません。
S：ほんの少しの違いですね。いずれにしても、音階は繰り返すわけだ。
S：その繰り返しを発見したのがすごいことなんですよね。
S：もう一つ気がついたよ。１２／５角形でドミソやドファラ、ソシレの和音をつないでみると同じ形の二等辺三角形になるよ。なぜだろう？
８、ギターの弦の間隔
S：ギターの弦はどちらの並び方なんですか？
T：ギターは平均律です。真ん中までは１２フラットあります。
S：このフラットの間隔が段々短くなっているようです。
T：平均律って、長さの比で分けるんではなく上の表のように２の指数で分けます。この考え方がまた面白い。全く数学的なのです。
さて、平均律については、【人間の五感は対数変換している】のページへ。
もどる