%２　【ユークリッドの世界】

『エラトステネスの仮説』

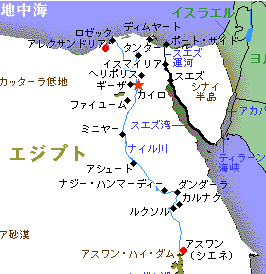
　二千年前の、エジプトのアレキサンドリアには大きな図書館があったという。ここに集った学者たちは、近代科学の先駆を成す成果を上げている。みんなも良く知っているアルキメデス、ユークリッド、エラトステネスなどだ。
--アルキメデスなら理科でならったよ。えーと、浮力の原理だ。
--確か、［エラトステネスのふるい］も勉強したことあるな。

この学者たちはお互に意見の交流や、遠く離れていても手紙の交換をやっていたらしい。そして、彼等はギリシャで生れたどちらかと言えばプラトニックな科学を実用化したり、応用しようとした。しかも、単なる応用でなく彼等には、一定の方向があったと思われる。これは想像だが、彼等の目的は、数学を使って宇宙を探る事にあったのではないだろうか。
--数学で宇宙が解るの？

　　その目的を支える発想とは、
(1)　できるだけ多くの自然現象を説明できるような、できるだけ少ない原理を見つける事。
(2)　自然の法則を見つけ、その原理で色々な現象を説明する事。
--理科のこと？
（この方針は、現代科学の根本原理ともなっている。）
　そして、このことを体系的にまとめた本が「ユークリッド原論」。これは読むと解りにくい本であるが、このユークリッド幾何学を宇宙を探るために用いたと思えば、なんと壮大な事ではないか。
--？

　ここで、エラトステネスという人を紹介しよう。彼は地球の大きさを求めたということで有名だ。彼の方法に対して、ぼくは壮大な同位角という名前を贈っている。

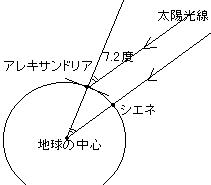
図　　夏至の真昼には
図　　大いなる同位角
図　　地球の大きさを測る

　毎年夏至の日には、エジプトのシエネでは真昼になると、井戸の底まで太陽の光が届きます。ところが、同じ日にアレキサンドリアでは太陽は、真上から７.２度傾いていました。彼は、地球が丸いことを知っていたので、この事から地球の大きさを測ることができると気がついたのです。
　まず、次のような図を考えました。地球を球だと考えて円で表します。太陽はずっと遠くにあるので、光線はほぼ平行に地球にやってきます。だから、緯度が違うと太陽の高度も違います。一方、旅人からアレキサンドリアとシエネの距離を聞いたら９２５�qとわかりました。
　さて、これでアレキサンドリアと地球の中心とシエネを結ぶ中心角の大きさが分かりますね。
--平行線の同位角だから７.２度になります。

そうすると、中心角と弧の長さからこの円の周の長さが分かる。これが地球の一周の長さだ。さあ計算してみよう。
--３６０÷７．２×９２５＝４６２５０�qだ。正確な値にずいぶん近い。
--ところで、シエネからアレキサンドリアまでの距離はどうやって測ったの。

それは、歩いて何歩か数えたのさ。
--そんなのいい加減じゃない。

伊能忠敬先生も、歩巾で測るのが一番正確だと言っているよ。
--ところで、不思議なことがあるんだけど、どうして彼はそんな昔に地球が(1)球だということを知っていたの。社会で昔の人は地球は平らだと考えていたとならったよ。
--それにさ、(2)太陽がそんなに遠くにあるなんてどうやって測ったの。

実にいいところに気がついたね。２０００年前の人達がそういうことを知っていたなんて信じられない気がするね。そこで彼等と同じ知識でこの２つの事が考えれるかどうかやってみよう。
まず、彼が知っていた現象として、夏至の日、シエネとアレキサンドリアでは正午の太陽の高度が違うという事実から考えてみよう。これをどう理解するかというと、実は二つの仮説が考えられる。それは、

仮説１
(1) 地球は球形である。
(2) 太陽ははるかかなたにあり、光線は平行。

　　　　　　　 遠くの太陽　　○　　　→　　　　→　　　　→　　   ○　丸い地球

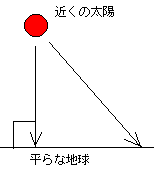
まったく逆のモデルとして      
仮説２　　　　　　　　　　　　　　　　　　　　　　　　　　             
(1) 地球は平。　　　　　　　　　近くの太陽　○　→　→　→ 　   |  平らな地球
(2) 太陽は近い。　　　　　　　　　　　　　　　　　　　　　　         

この２つの仮説はどちらでも前記の現象を説明できる。　

図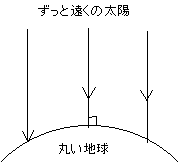　『何故、エラトステネスは仮説１を選んだのか。』

まず(1)の仮説について
地球が球である証拠を示すことができるかい？
--ひまわりの写真がある。

--海から陸地を見ると、始めは山の頂上、近づくにしたがって山の麓まで見える。

地球が球であるということは、今では当たり前になっているがそう簡単には証明できない。エラトステネスは地球を外から見る方法の代りに、地球の影を見る方法をとった。彼は月食が地球の影であることを知っていたのだ。地球の影は丸かった。
次に、(2)の仮説について
近いか遠いかを比べる時、二つの物を比べると解りやすい。その二つとは、月と太陽である。月が太陽を隠すくらいだから、太陽の方が遠くに在る事は解る。しかしどれくらい遠いのだろうか。ここでやはり月と太陽の関係を地球との三角関係で考えてみよう。
　図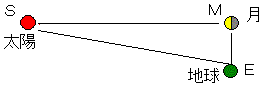
　
この△ＳＭＥはどんな三角形であろうか。その事を探るには、二角の角度が解れば十分である。∠ＳＥＭは計ればすぐわかる。したがって、もう一つ角度が解れば三角形の形がわかる。それには、月が半月になるまで待たねばならない。半月の時、∠ＳＭＥは９０度といえる。これで、この壮大な三角形の形がわかった訳であるが、∠Ｓは思ったより小さい事に驚くだろう。今日はちょうど半月で昼間に月が見えるから∠Ｅを計ってみよう。
--先生は測ってみたの。

うん。太陽も月も巾をもっているからしっかりと測れなかったけれど、この角度は８５度前後だった。この角が９０度に近いということはこの三角形が極めてとんがったものであることが解るであろう。つまり、太陽が月と比べて遠くにある事が解るだろう。その遠くにある太陽が月と同じくらいに見えるわけだから？
--太陽の方が月よりもずっと大きい。（月と太陽の見かけの大きさは同じである。地球から太陽までの距離が地球と月の距離の１００倍だとすると、太陽の大きさは月の１００倍になるはず。つまり、地球の２５倍である。本当は４００倍の距離！！）

月に写る地球の影からいうと、地球はその月の四倍ぐらいしかない。【月食から月と地球の大きさを求める方法】
--ということは、太陽は地球よりもずっと大きい。

その大きい太陽が地球の周りを回ることは？
--おかしい。

つまり、太陽を中心に地球が回っていると考えた方が自然である。そして、太陽ははるか彼方にありはるかに大きいから、太陽の光は平行だと考えてもいい。これで、エラトステネスが、仮説１を選んだ訳がわかったね。
--そんな昔にここまでわかっていたのか。それじゃあ、社会でならったのはどういうことだったのかな。

その後、アレキサンドリアの学問はヨーロッパでは忘れさられてしまったからだ。とにかく、アレキサンドリアの科学者たちが、幾何学（図形の勉強）が宇宙を探る重要な方法であることと考えていたのはうなずけるね。ところで、アレキサンドリアの科学者たちが目を向けていたのは宇宙だけではない。彼等は、身の回りの事にも数学を利用することを考えていた。
たとえば、アルキメデスなどは静力学に数学を利用している。


　　　てこがつりあうわけ　『アルキメデスとてこの原理』　
　アレキサンドリア学派が、ユークリッド幾何学を宇宙や自然を探る道具と考えていた事は前にも述べた。その例として、アルキメデスの事を挙げてみたい。彼の業績をいくつか挙げたいのだが、ここでは一つあげよう。
てこの原理を彼は、力の平行四辺形から証明したのだ。図→

参考文献　　
　　『玉川児童大百科事典』、『歴史的に見た数学概論』(岩田至康著）、『科学の形成と論理』板倉聖宜著
　　

　これらのやり方は、千何年の後に様々な人達が利用することとなる。たとえば、コペルニクスも地動説を称える時に使っている。ガリレオやデカルト、ニュートンも彼等から学んだのだ。

　『自然と数学はなぜ結びつくのか』
　
　アレキサンドリア学派のとった方法がその後の科学の方法を示している。アインシュタインの相対性理論もこの方法をとっている。できるだけ少ない原理でもって、論理的（数学を使って）に自然の現象を説明するという方法のことだ。これは数学を使って自然の法則を説明したり予測したりできるということを示している。ガリレオも「自然という書物は数学の言葉で書かれている」といっている。
--数学は役立っているのかなあ。

　『認識ののぼりおり』 　　　　（法則を見つけることと法則を応用すること）

小学生３年生の弟がいたとするよ。その弟が、「何故、縦×横で面積がでるの」と聞いたらどう答える。
--「そうなっとるからや。」と答える。

それでは、弟から馬鹿にされてしまうよ。こういう時は、うまい方法がある。それは、
「たとえば」を使う方法だ。例えば、縦が２�pで、横が３�pとすると。
--面積は２×３＝６。つまり、１ｃ�uの正方形が６個あるから。

１ｃ�uの正方形が何個あるのか出すためには、縦×横を計算すればいいということだね。
--３個の正方形が２列あるから３×２で計算できるということだね。これなら弟も納得するな。

弟の尊敬が、かちとれたかな。ところが、弟はさらに聞いてきた。長方形は分かったけど、平行四辺形も同じ様に計算するの？
--えーと。縦×横でいいのじゃないかな。

本当にいいの。この長方形をこうやって平行四辺形につぶしていくと？   （図　平行四辺形）
--あれ、面積がなくなる。わかった。縦でなく高さだ。

じゃあ、その理由を説明してよ。
--この三角形の部分を切り取って、こっちに移動させると長方形になり、横は変らないし縦は高さということです。

うまい。すでにわかっている長方形をちゃんと利用している。弟はさらに聞いた。
--しっつこい弟だな。　　　　　　　　　　　　　　　　　　　　

三角形の面積の出し方はどうなっているの。
--底辺×高さ÷２です。

なぜそうなるのか説明できる？
--この三角形をひっくり返してくっつければ、平行四辺形になる。底辺×高さで面積がでて、２倍したから２で割れば三角形の面積がでる。

弟は感心してさらに聞いてきた。台形の面積はどうやって出すの？
--（上底＋下底）×高さ÷２だったかな。

こういう公式になるわけを説明してみて。
--同じように台形をひっくり返して合せると平行四辺形ができます。底辺は上底と下底を合せたもので、２倍したから２で割ります。

上出来。長方形から平行四辺形、そして三角形ときてさらに台形へと、公式（法則）を見つけていったけれど、すでにわかっている事を使えば新しいことも説明できるということもわかったね。 ところで、この最後に出てきた台形の公式で長方形の面積を求めることができるだろうか。
--上底と下底が同じだから使える。あっ、それで２で割るのか。

三角形にもあてはめることができるかな？
--上底がないからだめじゃない。
--上底を０と考えればそのまま使えるよ。

三角形の公式で台形の面積を一度に求めることはできないけれど、台形の公式で三角形の面積は求めることができる。このように発見した公式（法則）は応用範囲も広くなっていく。
こういうように考える事を「のぼりおり」といい、私たちの考えは、こうやって深まっていく。（台形の公式は全てに当てはめることができる。）
--うちへ帰ったら、妹に教えてやろう。

さらに、このことは円の面積や扇形の面積を求めるのにも使える。ここに扇形があります。この周を直線にすると、扇形は？
--三角形になる。

面積は？
--底辺×高さ÷２＝弧の長さ×半径÷２
--扇形って、こんなに簡単に面積を求めれるのか。

円の面積も、まったく同じ様に求めることができるよ。
ここに揚匙にテープを巻いて作った円がある。この円の面積を求めるんだよね。そこで、この円を三角形に直してみるよ。この円をようじまで半分固定して、そして残りの半分を切る。
--三角形になります。　　　　　[円を長方形にする]リンク

この三角形の面積と円の面積は同じですね。では、三角形の面積は？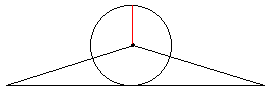
--底辺×高さ÷２。
--つまり、円周×半径÷２です。でも、円の面積は半径×半径×３．１４とならったよ。
--えーと、円周は直径×円周率だから、直径×円周率×半径÷２。さらに、直径÷２は半径だから、半径×半径×πだ。
--すごい！

☆ここで宿題をだすよ。今までの考えを使って、普通の四角形の面積を求める公式を作ってみてください。

　『多角形の外角の和』

（ロゴというコンピュータ言語がある。極めて簡単で、小学生にも理解できる言語であり、コンピュータを自分で動かしながらその働きをさぐれる。） このサイトからダウンロードできます。　「ロゴ情報室｣へリンク

今日は、コンピュータで図形の勉強をします。
勉強の相手をしてくれる動物を紹介します。
（ロゴをＲＵＮさせると亀がでてくる。）
--あれ、亀だ。かわいい。

この亀の名前はタートルと言います。このタートルは、命令するとおりに動きます。たとえば、［まえへ　５０］と命令すると、
--おっ！　前へ動いた。

［みぎへ　９０］と命令すると、
--向きを変えたよ。右へ９０度回転するわけか。すると、［ひだりへ　６０］は左へ回転するんだね。

じゃ、これで正三角形を作るにはどういう命令を与えたらいいのか。　　図　正三角形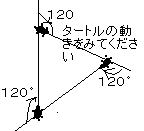
--ウーンと。［まえへ　１００］　みぎへ　えーと。　
--内角が６０度だから１２０度回転すればいいのか。
--それを３回くりかえせばできる。やった！
--３回くりかえせというのも命令できるの。

くりかえせ　３　[まえへ　１００　みぎへ　１２０]と書けば、[　]の中を３回くりかえすことになる。
　この１２０度を外角というんだ。ところで亀は何度回転したんだ？
--３６０度です。
--元へ戻っているから、一回転したことになります。

今度は正方形を、亀に書かせるにはどうしたらいいだろうか。
--外角を９０度にすればいい。

正６角形も簡単に作れるね。
--外角を６０度にすればいい。　図　外角の和から内角の和へ

今までやってきたことから、何か気がついたことない。
たとえば、ここに一般の六角形がある。この外角の和は何度だろうか。
--角を平行に移動して一ヵ所に集めると、ちょうど３６０度になる。
--亀さんに聞くともっと簡単に説明できます。亀さんは結局、この六角形の周りを外角の分だけ一回転するから３６０度です。
--あれ、すると六角形でなくても１回転するよ。

とすると、どんな法則（定理）がいえるの。
--どんな多角形でも外角の和は必ず３６０度になる。「外角の定理」

では、この定理を使って、正３６角形を作ろう。
--外角の和は３６０度だから３６で割ると、１０度になる。つまり、一つの外角を１０度にすればいい。
--この３６角形は、ほとんど円だね。

もう一つ応用をしてみよう。１０角形の内角の和は。
--三角形に分けると８個できるから、１８０×８＝１４４０度です。

--１０角形の中に点を取ってから、三角形を作ると１０個できる。点の周りの角は引けばいいから、１８０×１０−３６０でもいい。

--各辺を延長して、外角を足せば全て１８０度になるから、１８０×１０。外角の和を引けば内角の和がでるから、１８００−３６０＝１４４０。
--後の二つは考え方は違うけど、同じ式になるよ。

つまりこういう法則が成立つことになる。
法則　（　内角の和＝１８０×角の数−３６０　）

『正５/２角形を考えてみよう』　　分数の正多角形はあるか?!

Ｔ：正五角形をロゴで作図することはできるね。

S：エート。タートルにどれだけ右に回れといえば良いかというと・・・
S：外角の和は３６０度で正五角形だから、５で割ると・・・７２度にすれば良い。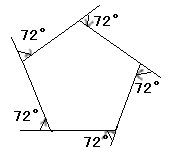

T：ではタートルに描かせてみましょう。自分がカメになったつもりで作図しても良いですよ。 ---　さて、正六角形は?

S：３６０度を６で割れば６０度だから、かめを６０度づつ右に曲げていけばいいです。

T：そうですね。正多角形を作図する時に、特にロゴで描くと、「外角の定理」を使った方がはるかに描きやすくなります。そして、この考えを使うと、なんと分数の正多角形まで作ることができるのです。例えば、正５/２角形を作ることもできます。さて、これはどんな形になるでしょうか?

S：正５/２角形なんてできるの?

T：これができるんだな。しかも、みんなの知っている形になる。

S：どうやってやるの?

T：正五角形と同じようにやれば良いのさ。外角＝３６０度÷Nでしょう。正五角形の時は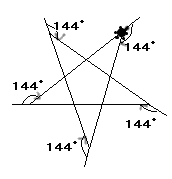Nは５、正六角形の時はNは６。とすると、正５/２角形のときは、N=５/２にすれば良い。

S：３６０÷（５/２）だから１４４度だ。すると、１４４°右へ回転すると・・・

参考 ： ロゴのプログラム
TO　正多角形　：角数　：分母
くりかえせ　：角数　[まえへ　１００　みぎへ　（３６０　/　：角数　＊　：分母）]
END

S：あれ、星型になる!　これが正５/２角形か。

T：数学の面白さはその意味を拡張（広げることが）できる所にあります。例えば、正の数を広げると負の数を見つけることができます。また、「×３＝３回たす」から 「×負の数」、「×分数」、「×少数」とドンドン「かけ算」の意味を広げたり深め たりすることができます。ここでは、正多角形を分数まで広げました。すると、分数の正多角形も考えることができるんですね。

　私はこのことを　岐阜物理サークル「のらねこ学会」　　　http://www.straycats.net/　　の村田憲治さんに教えていただきました。この文はのらねこ学会のサークルニュースvol.19に載った原稿からの引用です。

『　どんな多角形でも外角の総和は３６０度になる。このことから、正多角形の１つの外角を求めることができる。
例えば，正五角形の場合，　
　　　　　　　　　　　　　　　　　３６０度÷５＝７２度
この７２度を１つの外角として，次の図（その１）を描くことができる。
この関係を利用すると，正５／２角形なるものを描くことができる。
正５／２角形の場合，１つの外角を求めると，
　　　　　　　　　　　　　　　　　３６０度÷（５／２）＝１４４度
この「１４４度」の結果に従い，多角形を描くと「星形正五角形」になる。（図その２）
（村田註：「星形正五角形」とは，いわゆる５つの頂点がある星形のことです）このあと，例会では「正ｎ／２角形は描けるか」という問題に発展していきました。　』

S：正５/３角形はどうなるの?
T：ロゴに描かせて見たら。角数が５で、分母が３と。
S：あれ?　正５/２角形と同じだ。じゃあ、正５/４角形は?
S：あっ!これは正五角形と同じだ。でも、位置が違うよ。
S：内角はここだから・・・。この五角形は外側じゃない?。
S：すると、さっきの正５/３角形は正５/２角形の外側ということか。
S：つまり、五つの辺を持つ正多角形は正五角形、正５/２角形、正５/３角形、正５/４角形の４種類あるわけか。

S：ところで、星形正五角形の内角の和は１８０度で、外角の和は７２０度だろう。
S：このアイディアは多角形の外角の和を常に３６０度として考えているからおかしくないかなぁ。
S：それに辺も５つだし、５/２は何を意味しているんだろう。
S：正５/２角形の１つの外角は１４４°で角の数を２．５と考えたら。外角の合計は１４４×２．５＝３６０となるよ。

S：どんな小数も分数で表せるから、どんな少数の多角形もあるということかな。
S：正０．３角形って、角数を３として分数を１０にすればいいから、やっぱりどんな小数の多角形でもあるということだよ。

T：この分数多角形の内角の和を調べてみよう。
S：奇数の多角形で一番細かいの「（２ｎ＋１)/ｎ｣は、必ず１８０度になるんじゃない?
T：証明してみよう。
S：１８０（２ｎ＋１)−３６０ｎ＝１８０°だよ。
T：では、偶数の多角形の場合の一番細かいの「２ｎ/（ｎ−１)｣は?
S：１８０×２ｎ−３６０（ｎ−１)＝３６０°になるんじゃないかな。
S：正ｍ/ｎ角形の内角の和は、１８０ｍ−３６０ｎになる。
T：ｎ＝１なら？
S：１８０ｍ−３６０。そうか、ｍ角形の内角の和と同じだ。
S：この公式は、正多角形でなくっても成り立つよ。　　　　　　　　　
　【Ｌ３でいろいろな分数多角形を作ってみよう】 　 　分数正多角形・・・正２分の５角形とはどんな形？(Giogebra)

『分数多角形で葉のつき方を調べよう』

Ｔ：ジュン君はロゴを使って、色々な花を作っていたね。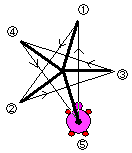
Ｓ：ハイ。バラとかさくらとか名前もつけました。
Ｔ：せっかくここまで勉強したんだから、夏休みのテーマ作品に植物の葉のつき方を、分数多角形で調べてみないかい？
Ｓ：どうやってやるの？
Ｔ：このヒメジョンの葉のつき方を見てごらん。葉は下の方から作られるだろう。それで、この葉に(1)とマジックで書くんだ。では、(2)はどの葉かな？
Ｓ：下から順番に書いていけば良いんだね。これが(2)だ。(3)はこれ。あれ、(6)は(1)と重なるよ。
Ｔ：そうだね。そこで、これを植物の上から見た図にしてみると、こういう５/２角形になる。つまり、(1)(2)(3)(4)(5)と回転して(6)で元にもどるわけだ。
Ｓ：サツマイモもそうだったよ。でも、どうして(1)(4)(2)(5)(3)の順番なの？(1)(2)(3)(4)(5)と並ばないのかな。
Ｔ：葉っぱの役目は何だった？
Ｓ：わかった！植物は葉で光合成をするから光が必要なんだ。だから、光ができるだけ当たるように回転しているんだ。
Ｔ：すばらしい。植物の智恵を解明できたね。では、外に出て、このやり方でいろいろな植物の葉のつき方を調べてみよう。
･････････（互生の葉を調べる）

Ｓ：トウモロコシは･･･。これは２/１角形だ。先生、トウモロコシはおかしいと思うよ。だって、これだとすぐに重なってしまって光が受けられないよ。
Ｓ：ひまわりは･･･。これも５/２角形だ。でもヒメジョンは上から見て右回りだったけど、ひまわりは左回りだよ。サツマイモも左回りの５/３角形。
Ｓ：あれ？この草は(9)が(1)と重なる。えーと、図に書くと、８/３角形だよ。（鬼百合・菊・桐・大根･白菜･幸福の木など)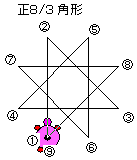
Ｓ：先生、質問。分数多角形の分母は何を表わしているの？
Ｔ：大事なことだね。実はこの２や３は茎の回りを回転する回数を表わしています。
Ｓ：どうして？
Ｔ：８/３角形は、八角点を３点飛ばしで一筆書きをして作図することを表わしています。だから、飛ばした点は一周してきて通るわけだから、その飛ばした点の数だけ回転するんですよ。
Ｓ：本当だ。この草は３回転している。
Ｔ：ここで、今まで調べた植物を整頓してみよう。
　２/１　　３/１　　５/２　　８/３　　･･･
Ｓ：この他にもあるのかなぁ。
Ｓ：分数でいうと、４/１や４/２があるけど、４/１は四角形だから、植物はこんな順番では絶対作らない。４/２は２/１になる。６は約分できる。７/２角形は葉っぱのつき方が不自然だ。でも、７/３角形はありそうだな。探してみよう。
Ｓ：９/２角形はありそうもないな。９/４角形もありそうもないよ。
Ｔ：ボクたちが調べたのはこれだけしかなかったけど、これを詳しく調べた人がいて、この他に、１３/５角形　もあるらしい。すると、１、１、２、３、５、８、１３、と並ぶ数が出てくるんだけど、１３の次は何かわかる？
Ｓ：前の二つの数を足しているんだ。だから２１。
Ｔ：そう。これをフィボナッチ数という。この数は植物のいろいろな所にあらわれてくるんだ。

　　　　【正ｎ/ｍ角形】　　　　　―――――　　【植物】
　１、　角数＝分子＝ｎ　　　　 ―――――　重なるまでの葉の数
　２、　分母＝ｍ点飛ばし＝ｍ―――――　重なるまでの回転数
　３、　外角＝３６０÷(ｎ/ｍ)　 ―――――　葉と葉の作る中心角（一定　130°＜Ａ＜145°）
　４、　分母の対＝ｍ、ｎ−ｍ　―――――　右回り、左回りの回転数

　　　【仮説：葉のつき方の原理（ルール）】
(1)　植物は、中心角が一定になるように葉をつける。
(2)　植物は、まんべんなく光や水が当るように葉をつける。
(3)　植物は、葉を重心がつりあうようにつける。

Ｔ：さらに、この分数多角形を使って、まつぼっくりを調べてみよう。

『まつぼっくりの研究』　　まつぼっくりを分数多角形で調べると・・・

参考文献　『形の周辺』清田圭一・千田稔著、『クンクン市のえりちゃんとロゴくん』戸塚滝登著、『折れ線の幾何』遠山啓著、『フラクタルって何だろう』高安秀樹･美佐子著

目次へ