四角形の面積の求め方（公式）
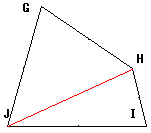
三角形に分けて面積を求める
S：台形までの面積の公式はわかったけど、台形でない四角形の体積を求める公式はあるんですか？
Ｔ：左の図のような四角形の面積をどうやって求めたらいいのか、ということですね。
S：そうです。でも、こんな四角形の体積を求める公式なんてないよね。
Ｔ：それをみんなで考えてみよう。公式とは何かを考えるいい機会かもしれない。さて、この四角形の面積を求めるには普通どう考える？
S：二つの三角形に分けます。三角形なら公式が使えるから。
S：この四角形をＪＨで分けて、ＪＨからの高さをそれぞれｈとｉとすると、
面積＝JH×（ｈ＋ｉ）÷２ で求まるよ。
Ｔ：でもね、この公式からは台形の公式は出てこないよ。台形の公式もふくむ四角形の面積を求める公式
はできないかな。
一般の四角形の面積を求める
S：台形を求めたときと同じようにやってみよう。
S：合同な四角形をひっくり返してくっつけると、左の図のようになる。
S：平行四辺形みたいだけど、へこんでいる。
S：このへこんでいるところをならせないかな。
S：横の辺の中点を結ぶと、面積は変わらないよ。
S：これで平行四辺形になったから、底辺×高さで求まるよ。
S：えっと、底辺を求めるには…。
S：縦の辺の中点どうしを結んでも、底辺と平行だよ。
S：これなら面積を半分にしなくってもいいね。
S：後は高さだ。中点から垂直に中線に下ろせばいい。
一般の四角形の面積の公式
S：できた。面積＝２ＡＢ×（ＣＥ＋FＤ）÷２＝ＡＢ×（ＣＥ＋FＤ）だ。
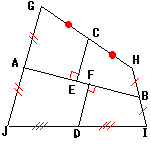S：中点連結の定理を使うと、この二本の垂線の長さは同じだよ。
S：どうして？
S：中点を結んでできる四角形ＡＤＢＣは平行四辺形だろ。だから、ＣＥ＝FＤといえるよ。
S：結局、面積は中点を結んだ線で求めることができる。
S：面積＝ＡＢ×ＣＥ×２
S：あれ、意外に簡単な公式だね。
Ｔ：よく出せたね。さて、問題はこの公式が、今までの公式も全て含んでいるのかということなんだ。
S：長方形でも台形でも中点を取ると、縦と高さになるから当てはまります。
S：三角形でも当てはまるよ。中点連結の定理で半分だから。
S：この公式はどんな四角形にでも使えるし、今までの公式を含んでいるんですね。
S：台形の公式はちょっと複雑だったけど、この公式は長方形と変わらないよ。
裏返すと長方形になる
Ｔ：そうなんです。この公式を見ると、この四角形を左図のような長方形に変えることができるということを示している。
S：そうか。周りを直角に切っていってつけたせば、できるんじゃないかな。
Ｔ：いやいや、そう簡単にはいかないよ。
S：そうか、でこぼこができるな。
S：さっきは平行四辺形になったもんね。
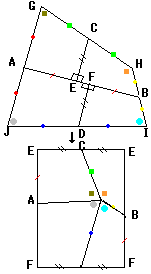Ｔ：実は、この中線や垂線にそって四角形を切って並べ直す（裏返す)と、長方形になるんだ。
S：パズルみたいだな。できた、長方形になる。不思議だな。
【四角形を長方形にする・・・四角形の面積を求める方法（ジオジェブラのシュミレーション）】
Ｔ：長方形になるから、四角形の面積＝AB×（CE＋FD）ということが改めて確かめられるね。
S：ところで、これ本当に長方形になるの？
Ｔ：そうだね。確かめなくっちゃ。
S：真ん中に集まる角は確かに３６０度になるな。
S：四角形にもなる。
S：４つの角がそれぞれ９０度だから、長方形だよ。
S：CEとFDは同じ長さだったから長方形だ。
S：それにしても、なんだか不思議だな。
台形の面積の公式にも当てはまる
S：ところで、さっき先生がこの公式から台形の公式が出てくると言ったけど、本当に出てくるの。
Ｔ：台形の二つの足の中点をとって結ぶと？
S：中点連結の定理で上底や下底と平行になる。
S：しかも、長さＡＢ＝（上底＋下底）÷２だ。
S：そうすると、高さをかけると面積が出る。
S：台形の公式＝AB×（CE＋FD）＝（上底＋下底）÷２×高さ
S：長方形や平行四辺形、三角形も、（中点を結んだ長さ）×（高さ）で求まるよ。
Ｔ：この公式は、台形の公式を拡げているんだ。長方形から出発して、平行四辺形、三角形、四角形へと面積の公式を考えてきたけど、拡げた公式はそれまでの公式を含んでいる。つまり、新しい公式が世界を広げているということが大切なことなんだ。
検地はこの公式を使っている
S：歴史の教科書の検地の絵を見ると、田んぼの辺の真ん中に棒を立てているんだ。
そして、上の図でいうとABの長さを測っている。
多分CDの長さも計るんだろう。それがなぜなのか不思議だったけど、今日やっとそのわけがわかったよ。
田んぼの面積をAB×CDで出しているんだ。
（これは正確な面積に極めて近い近似値になっている。また、絵によってはABの中点から直角になるようにCDを計ったと見られる絵もある。
これだと、ここで求めた公式で求めていることになる。
ジオジェブラで実際に調べてみてください。）
リンク【面白教材づくり】へ（四角形を反転させると？ 三角形の反転は？）→動画【はまぐりの数学別館へ】
目次へもどる