「新しい概念」はどのように認知されるのであろうか。「わかる」とはどういうことなのであろうか。
人工言語「LOGO」を開発したパパートは、自分の体験から、新しい概念を今まで持っている概念と関連づけていることに気がついた。
「…私は学習に関する基本的事実と考えられることを定式化し始めた。どんなことでも、自分の持っている内的モデルと同化させることができれば容易にできる。」
また、彼はこう言っている。
「我々は何かを知っている時、それを比喩的に知っている。」
このことを、彼の創った「LOGO」におけるプロージャ(手続き)の概念から見てみよう。
①正三角形を作る手続き(出会いの手続き)
・一つ一つ作る
まえへ 100
みぎへ 120
まえへ 100
みぎへ 120
まえへ 100
・繰り返しを使って作る
くりかえせ 3 [まえへ 100 みぎへ 120]
②正四角形、正五角形、正六角形、…、正星型五角形…を作る手続き(つながりの手続き)
くりかえせ 4 [まえへ 100 みぎへ 90]
くりかえせ 5 [まえへ 100 みぎへ 72]
くりかえせ 6 [まえへ 100 みぎへ 60] ・ ・ ・ ・ ・
くりかえせ 5 [まえへ 100 みぎへ 144] ・ ・ ・ ・ ・
③正n角形を作る手続き(一般化の手続き)
TO 正多角形 :角数
くりかえせ :角数 [まえへ 100 みぎへ (360 / :角数)]
END
④正分数多角形を作る手続き(拡張の手続き)nを分数にしたらどうなるだろう。
TO 正多角形 :角数 :分母
くりかえせ :角数 [まえへ 100 みぎへ (360 / :角数 * :分母)]
END
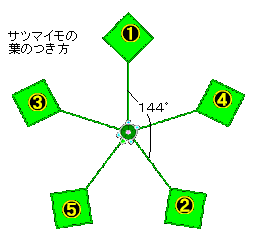
⑤サツマイモの葉のつき方のシミュレーション(利用の手続き)
サツマイモの葉は、つるのまわりを144度ずつ回転しながら出てくる。そして、ちょうど5つ目の葉が重なる。これはそのプログラム。
TO 葉
まえへ 100 ひだりへ 45
くりかえせ 4 [まえへ 50 みぎへ 90]
みぎへ 45 うしろへ 100
END
TO サツマイモ
いろは 4
えん 10
おそくなれ
葉
くりかえせ 4 [みぎへ 144 葉]
はやくなれ
END
この様にある手続きが学習者の頭の中に統合されるとその手続きには名前(葉)が与えられ、新たな手続きを作る際にはその名前(葉)を使って、新しい手続き(サツマイモ)が合成される。
しかし、新しい概念を既知のモデルに当てはめることはかなり難しい。「このことは何と関連しているのだろうか」「これと同じような事は今までになかったか」とはなかなか考えられないのである。上の例でいえば、一般の正多角形の「手続き」がわかったからといって、正分数多角形を考えれるわけではない。(③→④が難しい)
私の場合は、正星型五角形も一般化しようとして失敗している。いろいろ試したが、しばらくたって「正分数多角形」で紹介した様に外角を分数で割るというアイディアと出会い、この正分数多角形の一般化とつながったのである。そうなってみると、正分数多角形も外角で一般化できることになり、そうだったのかとわかる。
その場合、この「手続き」はさらに大きな「手続き」の概念でくくられる。わたしはそれを「出会い」「つながり」「ひろがり」の「手続き」と名付けている。
(1)「出会いの手続き」とは問題との出会いである。つながる問題(人)との出会いである。
(2)「つながりの手続き」とは三角形から四・五角形へつなげていったり、分数多角形につなげていくことである。さらに、それを自然や社会につなげていくことである。
(3)「ひろがりの手続き」とは一般化したり、拡張したり、他の人に伝えたりすることである。
そして、これは「わかる」過程でもある。 1999.8.6
【L3で分数多角形を作ってみよう】(「ロゴで遊ぼう」のページへ)
参考文献 「数学理解の認知科学」R.B.デーヴィス著、「数学教育とコンピュータ」J.T.フェイ編