%I１８ 　 【はまぐりの数学】

　数学は自然を抽象化したものです。しかし、抽象化のしっぱなしでいいのでしょうか。時には抽象化したものを、もう一度自然に帰してやることだって必要ではないでしょうか。その方法を「のぼりおり」と私はいっています。
　自然の中には数学がいっぱい溢れています。海のそこで寝ているはまぐりも、山の上であくびをしているまつかさも数学をしています。自然は数学をしているのです。だから私たちも数学をしているのでしょう。
　数学をするといっても、計算を紙の上でするのではありません。ここでは実物の貝を手に取って眺めながら、調べながら、実験をしながら考えを進めていきます。
　どんな現象にも法則があるものだということを、もう一度見てみましょう。そして、自然と数学の間を何度ものぼりおりしてみましょう。

　『相似と貝』
　
これは、はまぐりです。こちらはオウム貝です。さらにこれはさざえです。さざえのような貝を何と言いますか。
・・巻貝です。はまぐりは２枚貝。

このあわびは、何貝でしょう。
・・１枚貝。

えっ！　１枚貝なんてありませんよ。あわびは巻貝です。これらの貝は、一見して違った形のように見えますが、良く見ると共通した所があります。何でしょう。
・・殻でできている。
・・巻いている。

はまぐり（あさり）を一人ずつに渡しますから、よく見てください。実はこの貝の中に、今まで勉強してきた相似があります。どこにあるか探してください。
・・この貝をよく見ると、年輪みたいな模様が入っている。
・・その年輪は相似形です。

これは、この貝の過去の大きさと形を示している。一番小さいのは貝が開いたように上を向いているよ。
・・本当だ。

だから、貝は大きくなるのにこの形にそって、先の方をのばすように大きくなっていく。その時、でたらめに大きくなっているのではなく、形を変えずに大きくなるのです。
・・つまり、貝は小さい時と形をかえずに、相似になるように成長をしているということですね。

（なぜ相似になるのかというと、成長する時に殻の成分を分泌するのは、その時の貝自身である。つまり、分泌物は貝の大きさに比例するから相似になる。
このことは、人口の増え方にも言える。出生数は、その時の人口に比例する。）

だから、Ａの貝とＢの貝が相似になっているということなんですよ。
ところで、貝はなぜ形を変えずに大きくなるんでしょうか。
・・形が同じだと、内臓もそのまま大きくすればいいと思います。
・・貝にとっては住む場所の形が変らないということは、一部が狭くなったりするよりずっと住みやすいんだと思うよ。

では、この貝の成長の様子を実際に作図してみましょう。これは、大はまぐりを縦に切断したものです。切るのが大変でしたが、貝を横から見るためです。年輪ごとに印をつけていくと、どんな形になりますか。
・・三角形に近いです。

この成長にそって三角形を作ってみます。ただし、ちょうつがいの所の角度は等しいとします。さて、これらの三角形は？
・・相似です。
つまり？
・・角度がそれぞれ等しくなります。
何度ぐらい？
・・１２０度か１３０度ぐらいです。

という事は、この角度が全て等しいということになります。そこで、
この様に成長していくと、本当にはまぐりになるのか実験してみましょう。この線はさっきのちょうつがいの所の角度を表わします。全て等しく取ってあります。中心から５ミリの所から成長させていきます。成長する角度は１３０度にします。この特製分度器を使って相似になるように成長させていってください。
・・段々曲りぐあいがゆるやかになっていくな。
・・貝を当てはめてみるとぴったりだ。
・・巻貝はみんな右巻なんですか。左巻の貝はないんですか。

かたつむりも右巻しか見たことがないけれど、左巻のかたつむりもいるらしい。どっちでもよさそうなんだけど、片方に偏っているなんて不思議ですね。

さて、君たちはみごとにはまぐりになった。所で、今度はさざえやオウム貝になってもらおう。同じ座標で成長させてみてください。
・・今度は何度にすればいいのかな。

さざえの場合は９５度です。中心から５ミリの所から成長させてください。
・・さっきより、急に曲っている。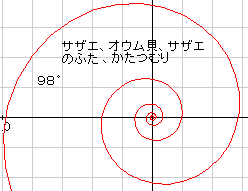
・・あれ、巻いちゃったよ。渦巻きだ。

なぜ巻くのか解りますか。
・・角度が小さいからだと思います。
・・角度によって巻方が違うんじゃないのかな。

　『角度による貝の分類』
　
その通り、先生もこのことに気がついた。この角度によって、貝を分類する事ができないかとね。これは大発見ですよ。
・・本当なの。

ただしさっきの様な作図だと、どうしても誤差が出てしまうので、
コンピュータで正確に作図させる事にしました。その図が、これです。９５度、１００度、１１０度、１２０度、１３０度、１４０度、
１５０度、１５５度、と作図させて、それを透明なシートに写してから、貝の上に乗せてどの角の曲線とぴったり合うのか調べたのです。
・・先生も暇やなあ。

たとえば、１５０度以上だと、うすっぺらい帆立て貝や、人間の爪がそうです。１３０度から１４０度が、はまぐりやしじみなどの二枚貝です。１００度から９５度では、エスカルゴやさざえ、オウム貝などの巻貝になります。
・・９０度はないのですか。

９０度だと円になります。所で、１２０度から１１０度の場合はなんになるのかわかりますか。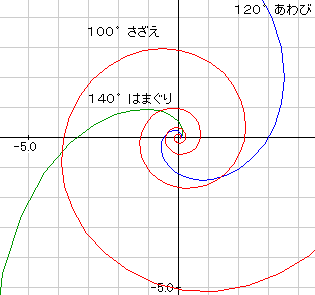
・・あわびじゃないのかな。

貝の等角らせんの角度による分類

９５゜〜１００゜
　　　巻き貝（さざえ,オウム貝,かたつむり）
１２０゜
　　　巻き貝（あわび）
１３０゜〜１４０゜
　　　二枚貝（はまぐり）
１５０゜〜１６０゜
　　　二枚貝（帆立貝,人の爪）

　『２枚貝の不思議』
　
こういう曲線を等角らせんといいます。そして、様々な生物に表われてきます。たとえば、ここにあるさざえの蓋も１００度のきれいな等角らせんを描きながら、自分の殻の成長に合せながら大きくなっていく。
ところで、巻貝は９５度から１００度だから、角度が小さく自分自身を巻く事ができます。だから？
・・殻で自分を守ることができます。

巻貝は自分を巻く事ができるがゆえに、殻はその役目を果しているわけです。ところが、２枚貝はその角度が大きい事によって自分を巻く事ができません。
・・それで、２枚の貝を使って自分自身を守っているのか。
・・賢いなあ。

等角らせん・・・【いろいろならせん（貝）を描いてみよう】（螺旋を自分で描けます）

左のサイト名は「つまようじでつくる橋のコンテスト」です。つまようじで橋を作るコンテストがあることを始めて知りました。奥が深そうです。このサイトの管理人である谷村さんが貝の螺旋を調べるソフトを作りました。貝の写真を取り込んで螺旋を描いていくことによって、貝の角度を調べるというソフトです。
アンモナイトや貝の画像を取り込んで、実際に螺旋を描いていくと夢中になります。微積分の見事な導入にもなっています。ぜひ、ダウンロードして試してみてください。

　『あわびの生き方』　　
　
ところで、あわびは巻貝なのですが、さっきの巻く角度が１２０度となっています。１２０度は、９５度〜１００度の巻貝と１３０度〜１５０度の２枚貝の中間の角度なのです。だから、この図の曲線の様にうまく巻けないのです。あわびはどうしたらいいのでしょうか。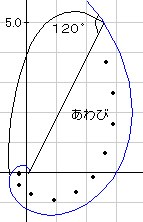
・・２枚貝のようにすれば？

ところが、二枚貝の様にもう一枚持ってくると、
・・巻いているところが邪魔だ。

つまり、２枚貝にはなれない。
・・巻貝にもなれない。

そこであわびは、岩に張付いて身を守るしかないわけです。
・・あわびも苦労しているわけだ。

　『コンピュータと貝』
　
・・先生。コンピュータにどうやって作図をさせたの。
実は、このらせんの式がある。その式を使って作図をさせたのさ。
ちなみに、その式とは　　ｒ＝ｋｅ^ａθ
・・この式はどうやって求めたの。

それは、後から教えます。
・・僕たちが作図したのもこの曲線になるの。

実は、正確な図ではない。というのは、貝は三角形の様に直線的に成長しているわけではないからだ。この三角形のちょうつがいの角度を無限に小さくしていくと上の曲線になる。これはあとで説明しよう。この曲線は色々な性質を持っている。たとえば、この曲線を何倍か拡大したのと、元の曲線はぴったり一致している。こういうのをフラクタルというのだよ。
ところで、上の式のグラフをコンピュータに書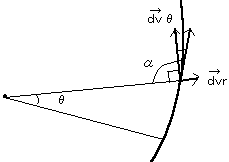 かせようとしても、うまくいきません。まず角度を入力してグラフを描かせるために、計算が必要なのです。     
ｒ＝ｋｅ^ａθ　において、点（ｒ，θ）でのベクトルＶを考え、その成分を回転方向と遠心方向に分ける。
　
　
　
これで、αを入力することにより、角度の違う様々ならせんを描かせることができるわけです。
今までやってきた分類の方法はコンピュータによる、シミュレーションを使いました。まず、いろいろな角度を入力してらせんを描きます。
それを、透明なビニールに書いて様々な形に当てはめてみる。ぴったり合うのが、そのらせんの角度となる。これを手でやろうとするととてもできなかったであろう。
・・コンピュータのいい所は、計算やグラフを書くのが早いということですね。

　『成長曲線』
　
巻貝がきれいならせんを描くことは解ったね。ところが、はまぐりに代表される二枚貝もらせんを描いている事はあまり知られていません。これは、巻いていないからなのですが、二枚貝も立派ならせんを描いているのです。
・・らせんは他にもあるんですか？

渦巻きのことさ。たとえば、かたつむりの渦。台風の渦巻き。夜空に浮ぶ銀河系外の渦巻き星雲、動物の角、爪。そういう物は、全て等角らせんなのさ。
・・それは貝と関係あるんですか。

もちろんある。あじさいの葉を食べているかたつむりや海岸べりの砂浜に潜り込んでいるはまぐりと宇宙にうかぶ渦巻き星雲とがこのらせんという曲線で結ばれているなんて不思議なことですね。

ここで、少し難しくなるけど、数学を使おう。高校で微分方程式というのを習います。それを使って、はまぐりの成長する曲線の式を求めてみます。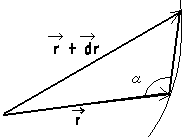

　求めたい曲線を極座標で 

ｒ＝ｆ(θ)　とする。
中心からはまぐりの殻までのベクトルｒを考える。

オウム貝やはまぐりは、成長しても自分自身と相似形になるから、これまでにやったように中心とのなす角が、常に同じである。
成長する方向のベクトルをとする。
　　　　　
等角であることから
　 　（aは一定、　となる。）
　
よって、f'(θ)＝af(θ)
この方程式を微分方程式と言う。この方程式の解は
　f'(θ)＝f(θ)となるf(θ)は
　f(θ)＝e^θ　だから、定数kをつけて
　f(θ)＝ke^aθ　となる。

・・高校へ行ったら習うの。

こういう曲線を成長曲線という。
成長というと、都市もまた成長している。子どもの頃、日本の主都だった奈良や京都、鎌倉は碁盤の目状の都市計画で作ってあるのに、江戸はなぜ碁盤の目状ではないのかと疑問に思った事がある。みんなにも聞こう。なぜ、江戸は碁盤の目になっていないの。
・・土地が、狭かったから。
・・関東平野だから広いよ。
・・丸くなっているからじゃないの。丸の方が長方形より楽だ。

丸は近い。まず、最初になにを作ったの。
・・江戸城。

最初は、その江戸城を中心にして、徳川家の旗本だけの小さい城下町だった。もちろん、長方形に碁盤目状に作ってある。ところが、参勤交代などで、大名の家臣などの武士が増えていく。まず、譜代大名をその周りに住まわせる。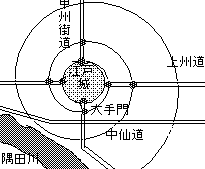
・・長方形を大きくしたの？

いや、江戸城の周りを回るように住まわせていったのだ。
・・それで丸いのか。

いや、そんなに単純ではない。まだ、外様大名がいる。その大名屋敷を、江戸城を中心にして、かたつむりのように「の」の字の形に、配置していったのだ。
（リンク【大江戸の町づくり】）
・・町人はどうしたの。

いい所に気がついた。武士は食うだけ。その武士を養う為に、膨大な数の生産者が必要となる。そういった職人や商人が住む所を、かたつむりが大きくなるように、配置していったのだ。さらに、かたつむりの殻に当たる物を、最初は堀、次に隅田川、江戸湾、そして神田用水という様に造り、はみ出さないようにしていった。こうしておけば、どれだけ人口が増えようが、町はどれだけでも大きくできる。
・・江戸時代に、江戸の人口はどれだけだったんですか。

当時、世界最大の都市さ。ロンドンやパリも及ばないくらいの都市だったんだ。人口が１００万人を越えていた。そうなったのは、このかたつむりの都市計画のおかげといっても良い。
・・徳川家康って頭がいいんだなあ。

　参考文献　　『江戸の町　上下』内藤昌著・草思社

　　『蜂が飛ぶ曲線』

蜂は花を見つけるとどう飛んで行くのか知っていますか。
・・真っ直ぐ飛んで行きます。

これが、真っ直ぐではないんだな。実は、らせんを描きながら飛んで行きます。蜂の目は複眼なので、目の中である位置に花を捕えたら、その位置を動かさないように飛んで行く。つまり、自分と花の角度を変えないように飛んで行くのです。
・・それで、花にたどり着けるんですか。

らせんには、中心があります。花が中心だから、渦を巻いて必ず花に到着することになります。花を目で捕えた時、複眼の中心からの角度が大きいと、巻貝の様ならせんになるし、中心から離れていないと、はまぐりの様ならせんになるのです。
・・蜂には、人間の様に真ん前がないんだね。
【９９、飛んで火にいる夏の虫・・・虫が火に向かって飛んでいく理由】

　『相似形』

貝や角や牙や植物が成長する時に、どういうように成長するんだったかな。
・・自分と相似になるように、大きくなります。

生き物にとって、相似というのは重要な意味を持っている。相似であるというのは大切なことに違いない。
・・合同よりも相似の方が大事ですね。

最近、フラクタルな図形とかが評判になっている。このフラクタルというのは、どれだけ拡大しても、相似になっているというような図形をいいます。自分自身と相似になっているのです。
・・貝のらせんはフラクタルなんですね。

　『成長に現れるｅのなぞ』

ｙ＝ｅ^xのグラフ

パイって何ですか。
・・おっぱい。アップルパイ。

違うよ。円周率のπのことです。πは円周を直径で割った値で、どこまでも割切れないけれど、数学では色いろな所にでてくる大事な数です。数学には、もう一つ大事な数があって、それがさっき出てきたｅです。ｅのことを自然対数の底といいます。
　
　　↑（これは元金1円、利率100％、期間1年に利息を無限回元金に組み入れる複利計算の元利合計の値。）
　連続複利法というのがある。元金Ａ、利率Ｘ，期間ｔとして、各瞬間に利息を元金に繰入れる複利計算の元利合計はＡｅ^xtで与えられる。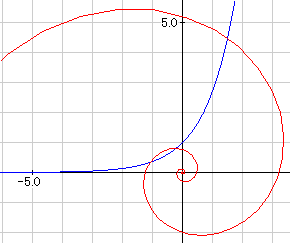
　利率をＸとする時、利率の繰入を頻繁におこなったものが e^x。

　
　一方、成長は、その時の自分を元金にして利息を出すようなもの。だから、成長の式はこの連続複利法の式にぴったり合う。
　その成長割合は、あらゆる瞬間において、成長している量の大きさに比例する。 言い換えると、如何なる瞬間でも変化率は、常にその瞬間の量の値と同じになる分数で表わされる。 これは、大きくなればなるほど、一層速く拡大する。 　例えば、人口の増加率が一定だとすると、人口増加のグラフはｙ＝ａｅ^rx（ｒは増加率）となり、この青いグラフのように急激に増加する。 これが人口爆発だ。

参考文献　『数学ゲームＩ』ガードナー著、『コペルニクスからニュートンまで』遠山啓著）

　『フィボナッチ数列と植物』

１２０２年、イタリアのピサの町に住むフィボナッチは次の様な問題を考えた。
「オス、メス１つがいの親うさぎが、毎月１つがいの子うさぎを生む。子うさぎは１ヵ月すると親になり、２ヵ月目から毎月、子うさぎを生み続けるものとする。１ヵ月目には、生れたばかりの１つがいの子うさぎが居るものとすると、うさぎはどの様に増えていくのだろうか。」

・・答え。うさぎのつがいの増え方は、１月ごとに
１,１,２,３,５,８,１３,２１,３４,５５,８９,…
となります。
・・まえの２つの数を足していけばいいんだ。１＋１＝２，１＋２＝３，２＋３＝５，・・・

　数をある規則のもとに順に並べたものを、数列といいます。上の様な数列をフィボナッチ数列といいます。式で書くと、Ｆn＝Ｆn-1＋Ｆn-2　となります。
　ところで、植物の葉のつき方にも法則があります。このフボナッチ数列が、枝に生える葉のつき方と関係があるのです。

図（「分数多角形で植物の葉を調べる」ページへ）

　葉のつき方や、ひまわりの種や松かさやパイナップルの菱形の鱗のようなものを見ていると、らせんとフィボナッチ数列がでてきます。なぜこんな数列や、らせんが出てくるのかを考えてみました。結局植物の成長はらせんなのです。そのらせんを、整数にするとフィボナッチ数列になるのではないでしょうか。
フィボナッチ数列も、前の数を足して成長しています。そして、兎の増え方から作った数列であるので、やっぱり成長に関係しています。
　ところで、角度が９０度ごとに、フィボナッチ数列が出てくるようならせんが有ります。このらせんの角度は何度かを調べてみました。107.034度

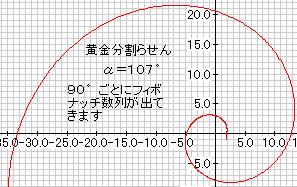
　このことから等角らせんにもフィボナッチ数列が表れることが分ります。

　『フィボナッチ数列の極限』
　
　ところで、このフィボナッチ数列の隣り合う項の比は、１．６１８・・・の黄金分割にどんどん近づいていきます。
たとえば、
１，１，２，３，５，８，１３，２１，３４，５５，・・・
　 　 　 　 　 　 　・・・＝１．６１８・・・＝
証明
フィボナッチ数の定義：Ｆ_n＝Ｆ_n-1＋Ｆ_n-2　をＦ_n-1で割る
Ｆ_n／Ｆ_n-1＝Ｆ_n-1／Ｆ_n-1＋Ｆ_n-2／Ｆ_n-1…(1)となり
Ｆ_n／Ｆ_n-1でｎを大きくしていったときにとる値をχとすると
Ｆ_n-2／Ｆ_n-1もχとなるから,(1)は
χ＝１＋１／χ　となる。両辺にχをかけて
χ×χ＝χ＋１…(2)
χ²−χ−１＝０を解くと,
χ＞０だから 　… となる。

また,フィボナッチ数列の一般項は
　　　となります。
証明は「フィボナッチ数列（Ｆ_n+1＝Ｆ_n＋Ｆ_n-1）を黄金分割（χ²−χ−１＝０）から作る」に

　『黄金分割を人は何故美しいと思うのか』
　
この長方形とこちらの長方形ではどちらが美しいと思いますか。
(正方形に近いのから、平たいのまで６種の長方形を見せて、集計したもの。）
・・黄金分割の長方形：Ｂ版画用紙＝１７：８

こちらの方の長方形を黄金比といい、昔から美しいとされていた。本当に美しいと感じるのか試してみたが、このクラスは多かったね。この黄金比は１：０.６８なんだが、この比がいろんな所にでてくる。たとえば、正５角形の同じ頂点を通らない２本の対角線は互に他を黄金分割する。
そして、このらせんにもこの比がでてくる。さっきやったフィボナッチ数にもこの比がでてきます。

そこで問題。
昔から、人類はこの比を、美しいものと感じてきたのはなぜか。

　私の説は、生物の成長の曲線を何百万年もの間、見てきた人類にとって、その極限である黄金比は、自然なものとして美しく感じるのではないかということなんです。
　今まで学んできたように、植物や動物の成長の曲線であるらせんの中に、整数比として出てくるのがフィボナッチ数列であり、その極限が黄金比だということになります。すると、黄金比は植物の枝や葉の中にあったり、貝の中にあったり、渦の中にあったりすることになります。それを長年見慣れている人類が、自然な形として、美しいと感じるのはもっともなことではないでしょうか。

参考文献　『黄金分割』柳亮著、『カーブ』ロックウッド著、『かたちのオディッセイ』中村雄二郎著、『ライフ・サイエンスライブラリー　数学の話』デビット・バーガミン著、
　　
_目次へ