「まつぼっくり」をロゴで作ってみよう

――「まつぼっくり」にどうしてフィボナッチ数が現れるのか――

S：質問があるんだけど、どうして、植物の種や葉にフィボナッチ数が出てくるんですか？

T：不思議ですね。私も１０年以上このことを考えてきたんですよ。これを探る為には、どうしたら良いのか考えてみましょう。まず、最初に幾つかの仮説を設定します。
(1)　植物はできる限り単純な法則で成長している。
(2)　植物は茎を中心に、光合成やバランスを最適にするように円運動をしている。
(3)　葉や芽は茎の周りを回転しながら順番に出てくる。その場合、回転の角度は１３７.５°の近く（１３５°〜１３８°）になる。
今までの分数多角形と葉や種の関係などから、この３つの仮説をつくります。

S：どうして、(3)１３７．５度なのですか。

T：それは分数多角形で考えてみよう。 バランスよく葉が出てくる分数多角形はどんな形だった？
　分数正多角形・・・正２分の５角形とはどんな形？

S：５／２角形、８／３角形、１３／５角形です。 えーと、葉の出てくる角度は、５／２角形なら１４４度。８／３角形なら１３５度。１３／５角形なら１３８．４６度だったよ。 あれ、１３７．５度に近づいていくような気がする。

分数正多角形の外角

T：同じくフィボナッチ数で出来ている、２１／８角形は１３７．１４度。３４／１３角形は１３７．６４７です。実は、このように一つとびのフィボナッチ数の分数多角形は、１３７．５０７…度　（一つとびのフィボナッチ数の分数多角形の極限は５／２，８／３，１３／５，２１／８，３４／１３，･･･，２．６１８だから、外角＝３６０÷２．６１８＝１３７．５）に近づいていきます。（計算は「はまぐりの数学」を参考にして下さい）
　上の表は、横が角数（分子）で、縦が分母の分数多角形の外角の大きさを表わしています（少数は四捨五入）。面白いことに角度が１３５°から１３８°までの分数多角形を選ぶと、フィボナッチ数の分数多角形になるんですよ。ただし、５／２角形は例外。７／３角形はバランスはまあまあですが、角度が１５４°と離れています。

S：１３７．５°ぴったりでなくても、１３５°〜１３８°までの角をとる分数多角形はフィボナッチ数を選ぶということなんですね。では、「まつぼっくり」はどうしてらせんができるのですか？

T：それは実験で確かめてみよう。

S：そんなことを実験できるのですか？

T：理科の実験とは少し違うけど、これもやっぱり実験のひとつです。それは、コンピュータによる実験です。植物の代わりにコンピュータにプログラムを与えて、そのプログラムでどのような成長をするのかを確かめるという実験（シミュレーション）をするんですよ。まず角度を入力すると、順番に中央から一定の長さのところに点を打っていくプログラムを作ります。次にそれを成長させるために、長さを少しづつ短くしていきます。ここで、これをロゴのプログラムにしてみると、次のようになります。うろこ点の数は１２６にしてあります。（これをコピーして、ロゴ坊で実行してみてください。）

てじゅんは　まつかさ　：角度
　　　でてこい
　　　ぺんをあげろ
　　　へんすうは　”ながさ　０
　　　へんすうは　”ふとさ　４０
　くりかえせ　１２６「へんすうは　”ながさ　（：ながさ　＋　１．５）
　　　　　　　　　　　　へんすうは　”ふとさ　（：ふとさ　−　０．２３）
　　　　　　　　　　　　まえへ　（２００　−　：ながさ）
　　　　　　　　　　　　ぺんのふとさは　：ふとさ
　　　　　　　　　　　　ぺんをおろせ　まえへ　０．１　うしろへ　０．１
　　　　　　　　　　　　ぺんをあげろ　うしろへ　（２００　−　：ながさ）
　　　　　　　　　　　　みぎへ　：角度」
　　　かくれろ
おわり

T：このプログラムを実行してみよう。そして、いろいろな角度を入れて、できた形を分類してみよう。その場合、上の表を利用するとわかりやすいよ。
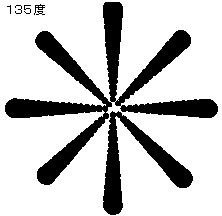
左の図はその一部。　【Ｌ３でこの図のまつかさを作ってみよう】

S：いろいろならせんができるよ。３本、５本、７本、８本、９本・・・。らせんができないのもある。１３５°だと８本の直線ができる。

T：なぜらせんができると思う？


S：１２０°や１４４°、１３５°の時はらせんにはならないよ。きっとその角度が少しずれると、らせんになるんだ。それに、らせんの本数は 分数多角形の角数（分子）になるよ。１２０°の近くの角度なら３本だ。１４４°近くなら５本だよ。

T：らせんの本数が７本や９本もあるのに、どうしてまつぼっくりは５・８・１３本になるんだろう。

S：さっき、分数多角形の角数と同じだけの数のらせんができるということがわかったよ。つまり、１３７°の近くの角度は、８／３角形や１３／５角形や２１／８角形に近い角度だからその角数の数のらせんができるんだ。

T：このように最初の仮説をもとにプログラムを作って実行させると、まつかさのと同じような模様ができるということは、この仮説がまんざら見当外れではないということを示していると思うよ。つまり、まつぼっくりの場合、１３７．５°で回転しながら種を作っていると言えるんじゃないかな。

【まとめると】

(1)　植物の葉のつき方は分数多角形で表わされる。

(2)　それを分類すると，２/１，３/１，５/２，８/３，（１１/４），１３/５，２１/８，３４/１３，５５/２１，・・・，２．６１８０３３９・・・となる。（ある植物の芽で１１/４[角度は１３１度]のを見つけた。このように例外はあるが，ほぼフィボナッチ数列となっている。）

(3)　なぜこの分数になるのか。分数多角形で調べてみると，(A)バランスがよい。(B)光がまんべんなく当るような順番。(C)外角が１３０°〜１４４°になっている。（例えば，７/３はバランスは良いが，外角が１５４°で外れている。）

(4)　つまり，角度が重要な要素であることがわかる。

(5)　その角度は，フィボナッチ数列の一つおきの比の極限となり，３６０°÷２．６１８…＝１３７．５０７…°に近づいていく。この角度は，葉が無限に重ならない理想的な角度で，黄金分割から出てくる角度である。

(6)　その角度でシミュレーションをしてみると，実際にまつぼっくりやパイナップルと同じ模様（らせん）が表れる。

(7)　そして，その時できる「らせん」の数は，その角の近似値を外角に持つ分数多角形の角の数になる。１３７.５°の角度で葉や芽や種が出てくるからフィボナッチ数列が出てくるともいえる。

目次へ