植物は黄金角(137.507度)を選んだ!
ほとんどの植物は137.507度(黄金角)で葉(種)を作っているといえる。
なぜなら,この角度で,全ての葉序のフィボナッチ数が表れることが数学的に証明できるから。
そのことを実際に示してみよう。植物の葉序は一つおきのフボナッチ数の分数として表わされる。その分数の極限値は黄金比になり,角度は137.507度となる。この角度で作った葉序を拡大すれば,全てのフィボナッチ数が現れる。
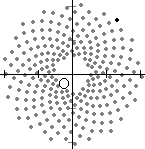
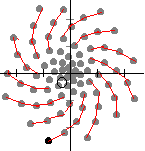
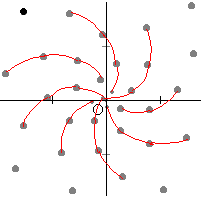
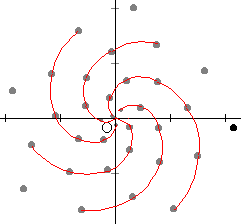
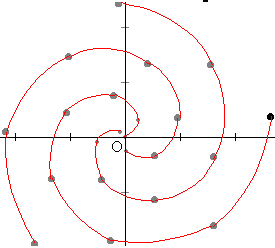
下の図は,角度137.507(黄金比 0.3820)で作った葉序(種序)。これを拡大していくと,順に・・・→34本→21本→13本→8本→5本→3本とラセンが表れる。このことから,植物は葉や種を出す角度として,それぞれ別々の角度を選んだと考えるよりも黄金角を選び,それぞれ植物によって拡大しているだけと考える方がすっきりしている。(でも,植物はどうやって黄金比を見つけたのだろうか?)
χ=a/50×cos(θ/360×2πa) y=a/50×sin(θ/360×2πa) でθ=137.507として,a=0,1,2,3・・・と点を打っていったもの。この図は「グラフソフトGrapes」(窓の杜でダウンロードできます。)で作ったもの。ロゴ坊は角度が不正確なのでGrapesを使った。
参考文献 吉田稔著『加工ジャガイモの作り方』農文教、『シュタイナー学校の数学読本』三省堂