%６ 【ガリレオと落体の法則】
図 ガリレオ・ガリレイ
(1564-1642) ７４歳まで長生きした。
図 ガリレオの見た月
図 木星の月
図 金星
『ガリレオ・ガリレイ』
この人の名前は、ガリレオ・ガリレイという。彼が持っている物は何だろう。
・・望遠鏡。
なぜわかったの。
・・どこかで読んだことがあります。
なぜ、望遠鏡を持っているんだろう。
・・初めて創った人だから。
彼も、自分で作ってはいるけど、初めて創った人ではない。
望遠鏡で初めて？
・・月を見た人。
そうです。望遠鏡で、隣の家を覗いていたのではない。彼はできたばかりの望遠鏡で、初めて宇宙を覗いた人なのだ。それでは、月に望遠鏡を向けて、何を見たと思う。
・・デコボコ。
それまで完全な球だと考えられていた月にも、山あり谷あり海ありということが解ったのだ。
・・そんなことが、大発見なの。
だって、天上の事と地上の事は違うと考えられていた時代に、月も地上と同じだという事を示したわけだから、キリスト教の教会の教えに逆らう大発見ですよ。
もう一つ、彼は木星を見ている。そこで、新しく発見した物は。
・・木星の衛星。
つまり、木星の月ですね。これが、なぜ大発見だったかというと、木星にも地球と同じ様に月があったということなんです。
・・木星と地球は同じ惑星ということか。
あと、金星を見ている。その金星で何を発見したと思いますか。
・・やっぱり、衛星なの。
いや、金星には衛星はない。彼は、金星が三日月に見えることを発見したのだ。ところが、火星や木星は三日月には見えない。この違いはいったい何なのか。
・・？
地動説の証拠になるのさ。僕は、彼を１７世紀最大のつっぱりだと思うんですよ。
『振り子』
彼は、自然をブラックボックスと考え、いろいろな入力をしてその出力によって自然の働きが何であるのかを調べたのです。
・・それは実験のこと？
理科では実験ともいう。ガリレオ＝ガリレイによる、落体の法則の研究は、自然の法則（関数）がまさにブラックボックスの様なものであり、彼はそれを調べる為に、繰返し実験を行ない、そのデータを整理して法則を発見したのです。
たとえば、彼の発見した法則の一つに振り子の法則がある。
君たちも同じ様に発見できるのかやってみよう。
彼は、お父さんの希望通りに医者になるか数学者になるか悩んだ結果、この法則を発見して、医学に応用し数学者になることを決めたという。
ここに同じ長さの振り子があります。大きく揺らすのと小さく揺らすのではどちらが時間がかかるでしょうか。
・・大きく揺らすと速くなる。
・・小さいと動く距離が少なくてすむ。
・・もしかしたら、同じではないかな。
（実験）
・・回数が少なければ、そんなに変らないな。
・・でも、なんとなく違うような気がするな。
同じ長さの振り子があります。一方の重りの重さを２倍にすると、どちらの方が時間がかかるでしょうか。
・・重いと動きが鈍いし、軽いと動きがすばやい。
・・今度も、同じではないかな。
（実験）
・・重い方が長くゆれているけど、変らないね。
・・でも、軽いのはすぐに止る。
振り子の長さを２倍にすると時間はどうなるでしょう。
・・時間は２倍になる。
・・変らない。
（実験）
・・長い方が１０回揺れる間に、短い方は１４回だ。
・・ということは、１．４倍だ。
振り子の長さを３倍にすると時間はどうなるでしょう。
・・３倍ではないな。
（実験）
・・長い方が１０回の内に、短い方は１７回。なんで１７なんだろう。半端だな。
振り子の長さを４倍にすると時間はどうなるでしょう。
・・あれ、１０回で２０回だ。ぴったり２倍。
今までやったことを、整理して法則を見つけてみよう。
・・表にするんでしょう。
長さＸ １ ２ ３ ４
時間Ｙ １ １.４ １.７ ２
・・もしかしたら、ＹはＸの平方根じゃないの。
もしその発見が正しいとすると、振り子の長さを５倍にすると？
・・２．２になるはず。
彼は、このことを発見して時間を振り子の長さで計れることを知った。そして、病人の脈を測るのに利用したのだ。
一説によると、彼は教会に医者になるべきか、数学者になるべきか悩みを神に聞いてもらいに来た。そして揺れる心と同様に、揺れるランプを見ながら、発見したといわれている。
・・ガリレオが振り子の揺れる時間を計るのに、何を使ったのですか。
・・脈拍じゃないの。
その通りです。脈拍は案外正確なのです。
・・でも、なぜ平方根になるのか不思議だね。
『ガリレオは実験して確かめたのか？』
図 【ピサの斜塔】ペーパークラフトで作れます(キャノンクリエイティブパークより)
ものが落ちるのは、物体が地球の引力によって引張られるためです。それならビー玉を１、２ｍの高さから落としたとしたら、その速さはどうなるでしょう。
・・ビー玉は、ずっと同じ速さで落ちる。
・・始めのうちは速くなるけど、すぐに一定の速さになる。
・・落ちてくる間じゅう、速さはどんどん増える。
実験してみよう。速さを調べるのにどうしたらいいか。ここでは速さを目で見るのではなく、耳で聞こう。３０㎝の高さから落とした場合と１ｍの高さから落とした場合の音の高さは、どうなっているか。
・・３０㎝と１ｍでははっきり違うけど、１ｍ前後の高さははっきりしないな。
同じ材質の鉄の玉があります。大きい方は１１０ｇ、小さい方は１５ｇ。この二つの鉄を同時に落としたら、どちらの方が早く落ちると思いますか。
・・重い方が、強く引張られているから、速く落ちる。
・・軽い方が、動きやすいから、速く落ちる。
・・同じ。
もう一つ予想してください。ピンポン玉と消しゴムの玉
では、どちらが速く落ちますか。机の上でやると、ほとんど同じです。
・・ピンポン玉の方が速い。
・・消しゴムの方が速い。
・・同じ。
では、実験をするから外へ出てください。３階から落とします。
いいかー。落とすぞー。
・・鉄は、軽い方が速かった。
・・２回目にやった時は、重い方が速かったよ。
・・はっきりとわからん。
・・消しゴムの方は、始めは同じくらいだったけど、ピンポン玉を追抜いた。
つまり、どういう結論にしたらいいの。
・・鉄の方は、実験では、はっきりと解らない。
・・ピンポン玉は、軽いから空気の抵抗を受けるんじゃないですか。
ガリレオは、鉄の実験の方は、こういう説明をしている。実験の結果は、重い方が速いか、軽い方が速いか、同じの３つしかない。ここで、重い方が速く落ちると仮定してみよう。彼は、どちらが速く落ちるのか調べるために、工夫をしている。それは、重い鉄と軽い鉄を糸で結ぶことだ。この糸は鉄でできており、軽く、丈夫で、どれだけでも短くできる。さて、仮定通りに重い方が速く落ちるとしよう。ひもで結んでいるので、全体としてはどうなりますか。
・・軽い方が後へ引張るので、遅くなります。
ところが、全体は重い方よりももっと重いから、仮定により重い方より速く落ちるはず。ひもで結ぶと、重い方より遅い。これは矛盾している。この矛盾はどこから出てきたのかというと、最初の仮定からだから、仮定その物がおかしいということになり、この仮定は間違っていることが言える。
・・？
今度は、軽い方が速く落ちると仮定してみよう。同じくひもで結ぶと、全体は重い方よりも速く落ちる。ところが全体の重さは重い方よりも重いわけだから、重い方よりも遅くなるはず。これは矛盾している。やっぱり仮定がおかしいから、この仮定は間違っている。
・・同じだとすると、結ぼうが速さは、同じだから矛盾しないわけか。
こういう実験を思考実験といいます。
・・なんか騙されたような気がするな。
じゃあ、軽いものでも空気を抜けば早く落ちることを実験してみようか。ここに取りい出したる透明なパイプの・・・
動画【空気を抜かない場合】【一本だけ空気を抜いた場合】
参考文献 仮説実験授業書「物の落ち方」
前にやった、振り子の実験を考えるよ。振り子の周期は糸の長さの平方根に比例するわけだから、この事を図に書くと右の様になる。ところで、振り子の振り巾が変っても時間はほぼ変らないわけだから、この様に相似な三角形にしても周期は変らない。
・・三角形ってどこですか。
本当は扇形だけど、三角形とみなせる。さて、長さが１の振り子が落ちていくのにかかる時間を１とすると、長さが４の振り子の時間は？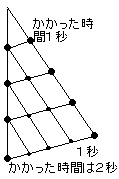
・・２倍です。
９の長さの振り子の時間は ？
・・３倍です。
長さが４の振り子が、１の三角形の分と同じ長さを最初に落ちる時間は？
・・１です。
とすると、残りの３の分を？
・・１の時間で落ちることになります。
さて、これを斜面に当てはめます。ガリレオは長さ６ｍの木製の斜面を作り、水時計で何年も実験をしています。今日は、先生の買ってきたカーテンレールを使って実験します。目盛は３０ｃｍごとに、うっておきましたが、どこの時間を調べたらいいでしょうか。
・・１と４と９です。
振り子の結果が正しいとすると、４の時は２倍、９の時は３倍の時間がかかるはずです。そこにしきいを置いて、音と目で時間を測りましょう。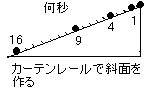
（実験）
・・ だいたい、２倍、３倍といえそうだ。
そこで、この結果を表にすると、
かかった時間 ０ １ ２ ３
ころがる距離 ０ ３０ １２０ ２７０
この式はどうなりますか。
・・かかった時間をＸとし、ころがる時間をＹとすると、Ｙ＝３０Ｘ2になります。
この式を翻訳すると、「斜面をころがる距離はかかった時間の２乗に比例する」という事になります。この事は、ガリレオが何十年かかって見つけたことです。それを、君たちはわずか１時間で求めたんだから、すごい。
・・式や表があるから、早くできたんじゃないかな。
・・振り子の場合は、Ｘを求める事だから、平方根になるのか。
・・でも、なぜ２乗に比例するんだろうな。
この斜面をもっと急にしていくと、この比例定数が大きくなるだけで、Ｙ＝ａＸ2という関係は変らない。そして、
垂直になった時の式が、
Ｙ＝４.９Ｘ2 となる。（Ｙはメートル、Ｘは秒。）
つまり、最初の１秒で約５ｍ落ちることになる。
ところで、月でも地球と同じ様に物が落ちていくわけだが、どの位の速さで落ちていくか知ってるかい。
・・月では、物の重さは地球上の６分の１になるというから、６分の１の速さじゃないかな。
地球上で６０㎏の人は、月では１０㎏になる。それは、月の引張る力が弱いからだ。したがって、月では物は地球と比べてゆっくり落ちることになる。式はＹ＝０.８Ｘ2
これから、君たちに月面上での物の落ちる様子を実際に見て体験してもらおうと思う。
・・ビデオで見るの？
ガリレオの研究によると、一定の時間に物が斜面を転がり落ちる距離は右の図のように円で表されるという。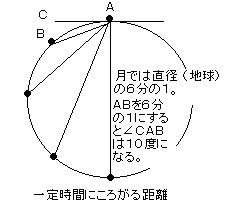
つまり、角度によって転がる早さが変るわけだから、月では何度になるか求めればいいことになる。僕の計算によると、この角度は１０度なのだ。
（カーテンレールを１０度に設定し、ビー玉を転がす。）動画
ただし、ちょっと首を傾けて下さい。
・・カーテンレールの上の方が真上というわけですね。
どう、この早さが月で、物が落ちる速さなのだ。
・・思ったより早いなあ。
【垂直落下と比べるシュミレーション（ジオジェブラで作成）
落体の法則と斜面・・・ターレスの定理を使った斜面を落ちるシュミレーション】
アポロの月面着陸をＴＶで見たことあるだろう。
・・知らないよ。
あれ、あっ。アポロは君たちが生れる前だねえ。
『パラボライド』
砲丸を投げたとき、どんな曲線を描いて飛んでゆくか書いてみて下さい。
・・半円になります。
・・半円ではなく、円のもっと上の方。
これは、実験で確かめることができます。ビー玉を７cmの高さから転がすと、秒速１ｍで真横へとび出します。面が水平だと、横へは０.１秒でどれだけ移動しますか。
・・０.１秒に１０ｃｍずつ移動していきます。
では、この面をとります。支えがないけれど、やっぱり横へは０.１秒に１０ｃｍずつ移動します。ところで支えがないので、ビー玉は下へ落ちていきます。どの様に落ちていきますか。
・・教科書の写真を見ると、０.１秒で５ｃｍ、０.２秒で２０ｃｍ…という様に落ちていきます。
そうすると、０.１秒後にはどこにあることになりますか。
・・右へ０.１ｃｍ、下へ５ｃｍのところにあります。
では、その点をとって線で結んでみて下さい。
・・これは、２次関数のグラフの半分ですね。
そうです。したがって、Ｙ＝ａＸ2の式で表わされます。
つまり、ビー玉が水平に飛んだ跡は、２次関数の曲線になります。さて、ここで、（パラボライドを取り出す。）
・・先生、そのすだれは何に使うのですか？
これは先生の作ったパラボライドというもの。
・・何をするの。
これで、砲丸の飛ぶ様子が分かるのさ。これはボールが水平に飛出した時に、どう飛ぶかを計算によって出したのを、ひもで吊り下げたのです。さっき計算したように、横へ飛ぶスピードは一定です。さて、これを上へ向けると、
・・あれ！ ２次関数のグラフになる。
ボールはこのように飛んでいきます。この様に物を投げた時にできる曲線を、放物線といいます。ところで、砲丸を投げる時、何度の角度で飛ばすのが一番飛ぶと思いますか。
【パラボライドで砲丸投げをしてみよう】（ジオジェブラ）
・・４５度じゃなかったかな。
それを、このパラボライドで確かめる事ができるのだ。２０度位だと、ここまで飛ぶ。だんだんと角度を大きくしていくと、飛ぶ距離も長くなる。ところが、
・・４５度を過ぎると、高く飛んでも距離は減っていく。
つまり、４５度が一番飛ぶということが分かります。このことはガリレオもわかっていたらしい。それを大砲を飛ばすことに応用しようと考えたわけだ。そして、自分の就職活動にこのことを宣伝している。
・・戦争を利用するなんて、きたないな。
当時、数学の研究だけで食べていくのは大変だったんだ。
だから、いやな戦争にでも役立つ事を宣伝しないと、支配者はお金を出さなかったのさ。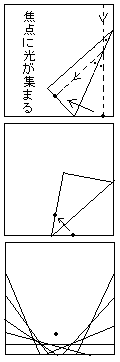
・・苦労したんだね。
『折り紙で放物線を作ろう。』
・・あれ、このプリントには何も書いてないよ。
良く見るべし。ちゃんと書いてある。
・・本当だ、点が一つ書いてある。
今日はプリントとこの点を使って、放物線を書いてみたいと思います。あとで、この点がいったい何なのか考えてもらいます。プリントの短い方の辺を、点に合せて折ってください。その折目を鉛筆でなぞってください。
・・辺を点に合せるんですね。ちょうど点と辺の真ん中に線が引ける。
折目を少しずらして同じように辺と点を合せるように折りましょう。
・・前の線と重なるよ。
交わってもいいのです。辺が終るまで点と重ねて折ってみてください。
・・この線の跡が放物線になっている。
・・じゃあ、この点はいったい何だろう。
まだ解りませんね。それでは、同じことを今度はこの円の折り紙でやってみましょう。
・・点はどこに取るんですか。
円の中心をはずして、適当に取ってください。できるだけ中心から離した方が面白いな。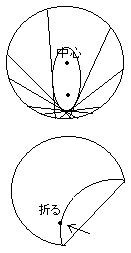
・・今度は円周を点に合せるのか。
・・やっぱり放物線になるみたいだ。
本当に放物線になるかな。
・・あれ、上の方で丸くなっている。これは楕円だ。
その通り、これは楕円になります。円のように丸いと上の方も丸くなるけど、さっきのプリントだと直線なので、上の方が開きます。でも、どちらも兄弟みたいな曲線です。(双曲線になるのはどういう時でしょうか）楕円は中心が２つある円です。
・・もう一つの中心はどこにあるの。
・・もしかしたらこの円の中心が、楕円のもう一つの中心じゃないの。
その通り。そして、この２つの中心は面白い性質を持っている。これは、楕円で作った水槽。アクリルで苦心して作ったんだ。さて、ここに水を入れてＯＨＰで写し、この中心にスポイトで水を垂らすと、
・・おっ！ 波紋が伝わっていって、もう一つの中心に集った。
・・かっこいい。（クリックすると、動画を写します。）
一方の中心から出た波が伝わっていって、楕円の壁に反射してもう一方の中心に集った分けだ。これは波ばかりではない。光や電波も同じように反射して一方の中心に集る。
・・この点は焦点だ。
その通り。この楕円を二つに切り離して一方を送信用のアンテナ、もう一方を受信用のアンテナとすれば弱い電波や声も伝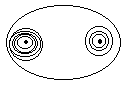
わってきて、強くできるわけだ。これは放物線も同じで、平行に来た光や電波をこの焦点に集める働きがある。
・・それで、衛星放送のアンテナは放物線になっているのか。
放物線のことをパラボラというので、このアンテナのことをパラボラアンテナという。（ここで風呂敷きに包んだソーラバーベキューを出す。）
・・その箱は何？
図 ソーラバーベキュー
これぞ、究極の省エネ。ソーラバーベキューさ。
・・先生が作ったの。
経費はアクリル板だけで、７８００円。なんせ、鏡のアクリルが高かったし、１枚失敗してしまったから、ちょっと高くついてしまった。
この曲げぐあいが難しかったのだ。なんといっても、放物線にそって曲げてから固定したんだが、その為にこの放物線と同じ曲線を板で切って、はさんで絞めつけて固定したのだ。
この放物線は、折り紙でやったように焦点をもっている。ここが焦点。この懐中電燈を垂直に当てると、光は反射してこの点を通る。
・・本当にバーベキューが焼けるの。
先生はとうもろこしを焼いてみた。真夏の１１時頃、表を焼くのに３０分、裏を焼くのに３０分、合計１時間。焼けたとうもろこしは実にうまかった。
懐中電燈の反射板をはずして、豆電球の所へタバコを置き、太陽に向けると１秒で火が付くよ。これは、台所で使うアルミのテープを使って、先生が作ったパラボナの反射板だがこれを太陽に向けて、焦点に手をおくと。
・・熱い。
図 パラボナ反射鏡
『２乗に反比例する関数』
さて、ここまではガリレオの研究。ガリレオが死んだ年に、イギリスに生れたニュートンという人がいる。この人はガリレオの研究を引継ぎ、なぜ２乗に比例するのかを明らかにした。これから、みんなでガリレオを越えよう。
ここに強力な磁石がある。（クリップを糸で結び、逆さにして引張ると、空中で止ったように見える。）地球も、この磁石の様に物体を引張っている。だから、磁石を研究すれば、地球の重力の事も解るはず。
ニュートンが考えた問題は、何か。
この磁石は離れると、引く力が弱くなる。たとえば、距離が２倍になると引く力はどれだけになるのだろうか。
・・２分の１になると思います。
実験をしてみよう。磁石の間にアクリル板を何枚か挟んで、ばねで引張る力を測る。さて、１枚挟んだ時に、ばねの伸びは３２㎜。２枚だと、ばねの伸びは８㎜。
・・４分の１だ。
・・どういうこと？
では、４枚挟むと・・・２㎜です。
・・表にしてみよう。
距離：Ｘ ０ １ ２ ３ ４
引力：Ｙ ３２ ８ ２
・・わからないな。グラフにしてみようか。
・・なんとなく、反比例みたい。
・・２の時は、４分の１。４の時は、１６分の１だ。
・・Ｙ＝３２／（Ｘ2）という式になる。
・・３の時を、予測してみよう。
・・Ｙ＝３２÷９＝３.５５５…になるはず。
（実験）
・・だいたい、３.５㎜だ。
すごい。完全にガリレオを越えている。この式を翻訳すると、「引力は距離の２乗に反比例している。」という法則になり、この法則は地球の引力にもあてはまる。そればかりか、ニュートンはこの法則が、全ての物体にも成立つといったのだ。
・・僕たちも、互に引張り合っているのか。
・・でも、なぜ２乗なんだろう。
教科書を見てごらん。そこに、明るさが距離の２乗に反比例するという例が出ている。
光が１ｍの距離に置いてある正方形に、当たっている時の明るさを３２ルクスとする。距離を２ｍにすると、この光は広がる。何倍に広がりますか。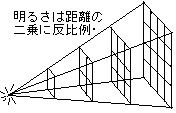
・・２倍です。
・・違うよ、面積は４倍だ。
つまり、同じ明るさが４倍に広がったわけだから、この元の正方形と同じ面積にあたる光の強さは、もとの？
・・４分の１になります。
同様に、３ｍになると９分の１です。
・・これも２乗に反比例だね。
これを引力にもあてはめることができる。光みたいに、引力の線が出ていると考えてごらん。
・・理科で磁力線の事をやったよ。
そう、その磁力線。それが光みたいに広がる。距離が２倍になると、あたる面積は？
・・４分の１。
距離が３倍、４倍になると。
・・９分の１、１６分の１。
・・地球の引力も、目に見えないけれど、線が出ているわけか。
『月はなぜ落ちてこないのか』
ニュートンは、月がなぜ落ちてこないのかという問題も解いている。木になっているりんごは落ちてくるのに、吊り下げられているわけでもない月がなぜ落ちてこないのか。実は、月もりんごと同じ様に地球に向って落ちつつあるというのがニュートンの答だ。
・・月は落ちてきているの。
・・いつ地球にぶつかるのですか。
計算によると、月は１秒間に０.１３６ｃｍずつ地球に向って落下している。
・・それだけならまだ大丈夫だな。
そうかな。１分間には、８.１６ｃｍ。１時間には、４８９.６ｃｍ＝約５ｍ。１日には、１２０ｍ
。１年では４.３２ｋｍ
・・えっ！
・・何年で、落ちてくるの。
ニュートンはこう説明している。高い山から大砲を射つと、弾はやがて落ちてくる。もっと強く射ち出すと、もっと遠くへ飛ぶ。しかし、やがて落ちてくる。もっと強く射ち出すと、もっと遠くへ飛ぶ。ところが地球は曲っているから、落ちてきた弾は、この様に地面に届かないことになる。そして、いつまでも落ち続けることになるのだ。月もこれと同じ。
【人工衛星をつくろう】logo 【惑星の楕円運動】giogebra
・・なーんだ。先生驚かさないでよ。
ところで、ガリレオやニュートンは神の存在を信じていたと思う？
・・ガリレオなんか教会に逆らったくらいだから信じていなかったんじゃない？
否、二人とも熱心なキリスト教に信者であり、神の存在を信じて疑わなかった。そればかりか、彼等がこんなに苦労して自然の法則を発見をしたのも「神が自然を創った」ということを証明したかったからなんだ。
ガリレオはこう言っている。
「神は二つの書物を書いた。その一つはいうまでもなく聖書である。もう一つは自然そのものだ。そして、それは数学の言葉で書かれている。」
ガリレオは自然の法則を探ることで神の意志を知ることができると考えていたのだ。そして、ここから科学が始まった。
・・キリスト教から科学が始まったということなの？
参考文献 『ぼくらはガリレオ』板倉聖宜著（岩波）、
『少年科学朝日』、『科学革命の構造』トーマス・クーン著、
『数学教室』西三サークルの実践、『天文の計算教室』斉田博著、『新科学対話』『天文対話』ガリレオ著、『円の兄弟』黒田孝郎著、『フル･ムーン』マイケル･ライト著、
目次へ