円錐の体積が円柱の１／３なのはなぜなのか
― シンプソンの万能公式 ―
中一の男の子が尋ねてきた。
S：先生は数学の先生だったよね。『円錐の体積が円柱の１／３なのはなぜなの？』
１、三角形と錐体を比べる
T：こういう時は、よく知っているものと比べながら考えるとわかるよ。錐体は何かと似ていない？
S：三角形だ。
T：そうだね。「三角形と四角形」は「錐体と柱」に似ている。
例えば、三角形は高さが同じなら頂点を変えても、赤い幅が変わらないし、全体の面積も変わらない。
錐体も同じで、高さが同じなら頂点を変えても、青い部分の形も面積も変わらないし、全体の体積も変わらない。 【ガバリエリの原理】
S：つまり、錐体は底面積が同じで高さが同じなら体積は同じになるということですね。
２、錐体は底面積が２倍になると体積も２倍になる
T：三角形は底辺が２倍になると面積も２倍になるね。では、錐体は底面積が２倍になったら、体積はどうなる？
S：底面積を２倍にした錐体を頂点から底面積が半分になるように切断します。切断した錐体の体積は同じなので、底面積が２倍になれば体積は２倍になります。
３、錐体の高さを２倍にすると、体積は？
T：では、錐体の高さを２倍にすると、体積はどうなる？
S：２倍かな？
T：そうです。錐体を２倍に拡大します。相似な２倍の錐体の体積は８倍。底面積は４倍。だから、元の底面積の錐体の体積は、８÷４で２倍になります。
つまり、錐体の体積は底面積と高さに比例するわけだから、錐体の体積＝底面積×高さ×ｋです。（ｋは定数）
これは、錐体の形によって体積が変わるのではなく、底面積と高さによっていることを示しているね。
４、円錐は三角錐の塊
T：さて、円錐は三角錐に分解できます。ということは、三角錐がどうなっているのか調べればいい。ところで、どんな三角柱も３つの同体積の三角錐に分解できます。
S：つまり、ｋ＝１／３ということですね。
T：高さが同じ三角錐は底面積を合計できるから、円錐の体積は円柱の１／３となる。
S：それはわかったけど、どうして１／２でなくて１／３になるのかがわからない。
５、１／２でなくて、１／３になる理由
T：１／３の意味か。これは難しい質問だ。例えば、
三角形の面積＝四角×１／２
三角錐体の体積＝四角柱×１／３ ではだめ？
S：どうして１／２ではないの？
T：積分の法則を使うと、
∫ｘｄｘ＝１／２ｘ2 （１／２ｘ2）'＝ｘ
∫ｘ2ｄｘ＝１／３ｘ3 （１／３ｘ3）'＝ｘ2 となるから。
S：難しすぎて、意味がわからない。
T：うーん。では究極の万能公式を出そう！
６、シンプソンの公式 （面積も体積も出せる万能公式）
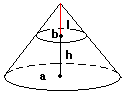T：ａ＝底面の面積 ｂ＝上面の面積 ｃ＝ａとｂの真中の面積 ｈ＝高さ とすると、
SorV＝（ａ＋ｂ＋４ｃ）／６×ｈ
という公式がある。この公式は、台の体積はおろか、三角形の面積まで求めることができる。
例えば、台形、半球を求めてみよう。
台形の面積＝（ａ＋ｂ＋4(ａ＋ｂ)／2）／６×ｈ＝（ａ＋ｂ）／２×ｈ
半球の体積＝（πｒ2＋３／４πｒ2×４）／６×ｒ＝２／３πｒ3
S：本当だ。すごい。
T：さて、この公式を使うと、
三角形の面積の場合は、ｂ＝０で、ｃ＝ａ／２だから、
Ｓ＝（ａ＋４ａ／２）／６×ｈ＝(１／２)・ａｈ
錐体の体積の場合は、ｂ＝０で、ｃ＝ａ／４ （２乗に比例する）だから、
Ｖ＝（ａ＋４ａ／４）／６×ｈ＝(１／３)・ａｈ
そうすると、４次元錐体の体積は、ｂ＝０で、ｃ＝ａ／８ （３乗に比例する）だから、
Ｑ＝（ａ＋４ａ／８）／６×ｈ＝(１／４)・ａｈ
となるはず。
S：へー。あれ、さっきの半球の体積は、底面が円で高さｒの円錐の２倍ですよ。
半球の体積＝（ａ＋４×３／４ａ）／６×ｈ＝（２／３）・ａｈ
円錐×２＝半球 円錐×３＝円柱 ということですか。
T：つまり、ｃがａに対して何倍になっているのかで、１／２か、１／３か、２／３かが決まるということです。
S：そうすると、ｃがａの１／４になる形の面積は、正方形の１／３ですね。
T：そうです。それはどんな形でしょう？
S：高さが１／２の時、幅が１／４になるのだから、二次関数のような気がする。
ｘ 0 0.25 0.5 0.75 1
ｙ 0 0.0625 0.25 0.5625 1 だから、グラフを反転させればＯＫだ。ｙ＝ｘ2の面積は正方形の１／３なんだ。
目次へもどる