円錐台の体積の公式
S：はじめまして。いつもホームページ読ませていただいてます。
さて、円錐の体積で教えてほしいことがあります。
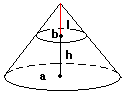
円錐を底面からhの高さで底面と水平にスパッと切った時の体積なのですが、真横からみると台形になる。この立体の底面(大きい円)の面積をa、上面(小さい円)の面積をb、とした場合、この立体の体積は (a+b)÷2×h でよいのでしょうか。
aとbが限りなく同じ大きさに近ずくと、それは「円柱」になるので、その体積は底面X高さで正しいと思います。
しかしながら、逆に上面bを限りなく上へあげると、上面の面積は限りなく０に近づき、その立体は円錐になります。
円錐の体積は a × h × (3分の1)ですから、２分の１ではありません。
前半の台形を立体にした体積の式を適応すると、円錐の時上面は点になり、面積は０だから (a+0)÷2
× h となり、底面積×高さ× 2分の1 になります。
どこがまちがっているのでしょうか。わからなくなってしまいました。 すいませんが教えてください。どうぞよろしくお願いいたします。
Ｔ：Yさん、こんにちは。とても面白い問題を考えましたね。円錐台の体積の公式なんて考えたことがありませんでした。
さっそく計算してみました。
ずばり、あなたの仮説である、（ａ＋ｂ）×ｈ÷２ は、あなたが指摘しておられるように、矛盾があります。
（でも、こういう仮説を持ったことがすばらしいし、その矛盾に気がついたことは、もっとすばらしいです。）
正しい公式は （ａ＋ｂ＋√ａｂ）×ｈ÷３ です。
円錐台の体積の求め方は、底面積ａの円錐の体積−底面積ｂの円錐の体積です。
単純に（ａ＋ｂ）の半分の円柱にするのでは、円錐の性質上おかしなことが出てくるからです。
まず、切りとった円錐の高さｌを求めます。
ｌ：√ｂ＝（ｌ＋ｈ）：√ａ なので、
ｌ＝ｈ√ｂ÷（√ａ−√ｂ）となります。
次にさっきの円錐台の体積を求めてみます。
大きい円錐の高さは、ｌ＋ｈ＝ｈ√ａ÷（√ａ−√ｂ）となり、
円錐台の体積＝底面積ａの円錐の体積−底面積ｂの円錐の体積に当てはめると、
Ｖ＝ａ×ｈ√ａ÷（３×（√ａ−√ｂ））−ｂ×ｈ√ｂ÷（３×（√ａ−√ｂ））
＝ｈ（ａ√ａ−ｂ√ｂ）÷（３（√ａ−√ｂ））
＝ｈ（√ａ×√ａ×√ａ−√ｂ×√ｂ×√ｂ）÷（３（√ａ−√ｂ））
＝ｈ（√ａ×√ａ＋√ａｂ＋√ｂ×√ｂ）÷３
＝（ａ＋ｂ＋√ａｂ）×ｈ÷３
となります。
この公式なら、ａとｂを同じにしても、ｂを０にしても矛盾は出ません。
でも、√ａｂが出てくるところが面白いですね。
シンプソンの公式
この式を見ていると、ａとｂはわかりますが、√ａｂが何を示しているのか気になります。
そこで、ａ＋２√ａｂ＋ｂ＝√ａ＾２＋２√ａｂ＋√ｂ＾２＝（√ａ＋√ｂ）＾２と考えると、
（ａ＋ｂ＋√ａｂ）＝（ａ＋ｂ＋（√ａ＋√ｂ）＾２）÷２となり、
Ｖ＝（ａ＋ｂ＋√ａｂ）×ｈ÷３＝（（ａ＋ｂ＋（√ａ＋√ｂ）＾２）÷２）×ｈ÷３
＝（ａ＋ｂ＋（√ａ＋√ｂ）＾２）×ｈ÷６となります。
一方、ｃ＝（√ａ＋√ｂ）＾２）÷４は円錐台の高さの中央における断面積です。
（∵上底と下底の半径の長さの比は√ａ：√ｂなので、中央の円の半径の長さは（√ａ＋√ｂ）／２となり、面積はその二乗になるから。）
そうすると、先ほどの式は、
Ｖ＝（ａ＋ｂ＋（√ａ＋√ｂ）＾２）×ｈ÷６
＝（ａ＋ｂ＋４ｃ）×ｈ÷６ となります。
これが、「シンプソンの公式」です。（積分で出てきます。）
ｈ＝立体の高さ、ａ＝立体の下の底面積、ｂ＝立体の上の底面積、ｃ＝高さの中央における断面積という実に簡単な式です。
この式に当てはめれば、円柱や円錐の体積はおろか、球の体積でも、平面図形の面積でも求めることができる万能の公式です。実際に当てはめてみてください。（新しい公式はそれまでの公式を含む。）
S：この公式は円錐台から作ったのだから円柱や角錐、円柱に当てはまるのはわかるけど、どうして球の体積も求まるのですか。
Ｔ：不思議ですねぇ。そういえば、半球だって求まりますね。
S：あれ？この公式は面積の公式にも当てはまるよ。
S：本当だ。ａやｂを底辺にすれば、三角形や台形の面積も求まる。
S：どうしてだろう？
シンプソンは１８Ｃ．のイギリスの人で、独学で数学を学習し、後に大学の教授になった人です。この公式は、一次、二次、三次関数については正確な値がでます。４次以上についてはわかりません。球の断面の面積は二次関数になるので当てはまりますが、円の断線は無理関数になるので当てはまりません。参考【円錐の体積はなぜ円柱の１／３なのか】
参考文献 「授業を楽しくする数学の話」片野善一郎著・明治図書