�T���N�g�y�e���u���N�̃p���h�b�N�X�i�������Șb�j
�\���Ғl����o�ϊw�ց\
�P�A�M�����u���ŕK�����Ă���@
S�F�M�����u���ŕK���ׂ�����@����������B
S�F�ق�Ƃ��B�ǂ�ȕ��@�Ȃ́H
S�F�Ⴆ�A���[���b�g�ŐԂƍ��ɓq���邾��B���m���͂P�^�Q�B�܋��͓q�������z�̂Q�{�B����ōŏ���100�~�q����B������������A���͂Q�{��200�~��q����B����ɕ������玟��400�~�B��������ĕ�������{�X�Ƃ����Ă����āA���������ł�߂�B��������A�K��100�~�ׂ͖���B
S�F�ǂ����āH
S�F�����āA����܂ŕ������Ƃ���ƁA
���v���z��100�~�{200�~�{400�~�{�c�{�Qn�~100�~
�@�@�@�@��100�i1�{2�{4�{�c�{2n�j
�@�@�@�@��100�i2(n+1)�|1�j
�ł���B������A���̎��ɏ��ĂA�Q(n+1)�|(�Q(n+1)�|�P)���P�ƂȂ�A100�~�ׂ̖��ƂȂ��B
S�F100�~�ł͏��Ȃ���B
S�F������A�ŏ���100�~�̑����100���~�ɂ���A�K��100���~�ׂ���Ƃ������ƂɂȂ�B����ɁA���Ƃ����Ȃ����z�ł�������J�Ԃ��Α傫�Ȃ����ɂȂ��B
S�F�ȂςȋC������ȁB���܂ł̂�������ʂɕK�v����B
S�F�ł��A�m���P�^�Q�Ȃ�A��������������邱�Ƃ͂Ȃ���B
S�F���ۂɂ���Ă݂��́H�@�����Ă�̂��킩��Ȃ�����A�����������Ȃ�����A�E�g����B���̕��@�́A�������łȂ��ƃ_������B
S�F�R�����玟�͂W�O�O���~���B���v�P�T�O�O���~�K�v����B
T�F�ʔ����˂��B�������Ă݂����Ȃ�悤�ȕ��@���ˁB���͂���Ƃ悭���Ă���q���̖�肪�̂��炠��B�l�����l�̓_�j�G���E�x���k�[�C�B
�Q�A�T���N�g�y�e���u���N�̃p���h�b�N�X
T�F�x���k�[�C�́A���̂悤�ȃR�C�������Q�[�����l�Ă����B
�w����l���A�����ȃR�C�����A�I���e���o��܂œ���������Ƃ���B�I���e���o����Q�[���͏I���B�I���e���o���̂���P��ڂȂ�Q�O�O�~�A��Q��ڂȂ�S�O�O�~�A��R��ڂȂ�W�O�O�~�A�c����ڂȂ�͂P�O�O�~�Qn�~�A�Ƃ����悤�ɁA�܋��z���{�X�ɑ��傷��B���āA���̓q���̎Q�����Ƃ��āA������܂Ŏx��������悢���B�x
S�F���z�̑������́A�������ƈꏏ���ȁB
S�F�Q�����Ƃ��ĂP�O�O�O�~���炢�Ȃ�o���Ă��������ȁB
S�F�P���邾���ł���B���������Q�E�R��ŕ\���o���B�T�O�O�~���炢���B
S�F���Ⴀ�A�Q�[�����瓾���闘���̊��Ғl���v�Z���Ă݂悤�B
�@200�~�����炦��m���́A1/2
�@400�~�����炦��m���́A1/4
�@800�~�����炦��m���́A1/8
�@�E�E�E�@
S�F���z�������Ȃ�ɂ��������Ċm����������킯���B
T�F�ł́A���Ғl���o���Ă݂悤�B
���Ғl��200�~1/2�{400�~1/4�{800�~1/8�{�c�{100�~2n�~(1/2)n�{�c
�@�@�@��100(2�~1/2�{4�~1/4�{8�~1/8�{�c�{2n�~(1/2)n�{�c)
�@�@�@��100(1+1+1+1+�c)�����@�@�@�E�E�E(1)
S�F�����A������I�B�ǂ����āH
T�F�����ȂB���җ����̑傫�����画�f����A�u�ǂꂾ���Q�������Ă��Q�[���ɎQ�����ׂ��v�ƂȂ�B
S�F����������B�Ⴆ�P���~�����ĂQ�O�O�~�������炦�Ȃ��Ƃ������������B
S�F����A�P�O��ڂɕ\���o��A�P�O���Q�S�O�O�~�B�Q�O�ƂP���S�W�T���V�U�O�O�~����B���ꂷ�����Ȃ��B
S�F�ł��A�X��������o�����邱�Ƃ͂Ȃ���B
S�F����A�i1/2)9��0.002��0.2���قǂ����B
S�F�ł��A������͂Ȃ���Ȃ��H
S�F���̊��Ғl�����������B
S�F���Ғl��������Ƃ������Ƃ́A���������Ă���ΕK���P���~�ȏ�ׂ̖�������Ƃ������ƂȂ́H
S�F1���~�ǂ��납�����~�ȏゾ��B
S�F�ł����A�q����x�ɂP���~�K�v�Ȃ�B�|�����������Ă�����B�����ɖׂ���Ƃ͎v���Ȃ���B
T�F���̖��͂��܂�ɕςȂ̂Łu�T���N�g�y�e���u���N�̃p���h�b�N�X�v�ƌĂ�Ă���B���V�A�̓s�s�̖��O�Ȃ��ǁA�����Ńx���k�[�C�����̖��\�������炾�B
S�F���Ғl��������Ȃ̂ɎQ�������ǂꂾ���ɂ���̂��ƕ����ƁA������ɂł��Ȃ��Ƃ����Ƃ��낪�p���h�b�N�X�Ȃ�ł��ˁB
S�F���Ȃ�ǂ��l���Ă��U�O�O�~�ȏ�͏o���Ȃ��ȁB
�R�A���ۂɎ������Ă݂悤
S�F�ǂ����s�v�c���B�������Ă݂悤�B�\�~�ʂł���Ă݂��B
�@�@��ځ@ ���z�@�@�@���v���z
�@�@ 1�@�@�@200�@�@�@32�@�@ 6400
�@�@ 2�@�@�@400�@�@�@20�@�@ 8000
�@�@ 3�@�@�@800�@�@�@10�@�@ 8000
�@�@ 4�@�@ 1600�@�@�@ 3�@�@ 4800
�@�@ 5�@�@ 3200�@�@�@ 1�@ �@3200
�@�@ 6�@�@ 6400�@�@�@ 1�@ �@6400
�@�@ 7�@�@12800�@�@�@ 0�@�@�@�@0
�@�@ 8�@�@25600�@�@�@ 1�@�@25600
���v�@�U�W��ŁA���v���z�@�U�Q�C�S�O�O�~�B���ςX�P�W�~
S�F�T�O�O�~�̎Q�������ƁA�Q�W�S�O�O�~�ׂ̖����B
S�F�ł��A�Q�������P���~���Ɗ��S�ɑ��ł��傤�B
S�F���Ғl���猾���A�𑝂₵�Ă������тɕ��ϋ��z�͂ǂ�ǂ��Ă����Ƃ������ƂȂ�ł��ˁB����s�v�c�B�����ɂȂ������ς��B
S�F���w�肷��A���Ғl�����߂邱�Ƃ��ł��邩����Ȃ��̂���Ȃ��B
T�F�������邱�Ƃ͐l�ԂɂƂ��ĕs�\����ˁB�ł��A���w�肵�Ȃ��Ƃ���ς�p���h�b�N�X�͎c��ˁB
S�F�x���k�[�C����́A���̖����ǂ��������̂ł����H
�S�A�x���k�[�C�̉�@
T�F�x���k�[�C�́A�q���Ɏx�����������������z�ł��A���̐l�̎����Y�Ƃ̊W�Œl�������Ⴄ�Ƃ������Ƃ����w�I���Ғl�̒�`�ł͖������ꂽ�̂ŁA�p���h�b�N�X�����������̂��ƍl�����B
S�F�Ӗ����킩��Ȃ��B
T�F�Ⴆ�A�����P���~�A�b�v�Ƃ����Ă��A�����[������̂P���~�A�b�v�̒l�����ƁA����10���~����̂P���~�A�b�v�̒l�����Ƃ͓����ł͂Ȃ�����B������A�q���̊��ҋ��z�́������ǁA�Q���҂��܋�����閞���̓x�����́��ł͂Ȃ��ƍl�����̂��B
S�F�m���ɁA������ɂ����������Ă��A������������ɂȂ�Ƃ͌����Ȃ�����ˁB
T�F���ۂɁA���̓q���ł�����Ȃ�q���܂����Ƃ�������������ƁA�U�O�O�~�Ƃ�����������ԑ����炵���B���Ғl��������ɂȂ邱�Ƃ������Ă��ς��Ȃ��Ƃ����B
S�F����S���w�̖��Ƃ��Ėʔ������B
T�F�x���k�[�C�͂��̖����̓x�������A���Y�̍����ɂ���ĕω��������������z�̗^���閞���x�͎��Y�z�ɔ���Ⴕ�Č�������Ɖ��肵���B��������ƁA�����x�͋��z�̑ΐ����Ƃ邱�Ƃŕ\���ł���B
S�F�Ȃ��ΐ����Ƃ�́H
T�F����́A�t�F�q�i�[���E�G�[�o�[�̖@���𐔎�������Ƃ��ɂƂ������@�ƑS�������ȂB
�y�P�O�P�A�l�Ԃ̌܊��͑ΐ��ɕϊ�����Ă����z���Q��
�s�ȒP�Ȑ����i�ؖ��j�t�@�@�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
���Y�z�F�v�A���̑����F���v�A�v�̗^���閞���x�F�t�i�v�j�A���̑����F���t�Ƃ���B
���Y�̑����ɑ��閞���x�̑����́A���Y�z�ɔ���Ⴕ���Y�̑����ɔ�Ⴗ�邩��A
�@���t��k�E���v�^�v
�����ŋߎ�����ƁA
�@���t�^���v��k�^�v
�����ϕ�����ƁA
�@�t��k�Elog�v�{�b�@�@�E�E�E(2)
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
S�F�l�Ԃ̊��o�͎h�����傫���Ȃ�Ɗ��������݂��Ȃ��Ă���Ƃ����̂��A�����̋��z�ɂ����p�����̂ł��ˁB
T�F��������ƁA���Y�v�̐l���Q���������Ă��̓q���ɎQ���������A�\������ڂɏo��A���̎��Y�́i�v�|���{�Qi�j�S�~�ƂȂ�B�i���܂ł̂䂫�������A�S�~�P�ʂɂȂ��Ă���j
�����āA
�����x�t�������Elog�i�v�|���{�Qi�j�{�b
���Җ����͂��̒l�Ɋm���������Ă����B�i���Ғl�Ɠ����j
�@�d�t��(�t1�~1/2�{�t2�~1/4�{�t3�~1/8�{�c�{�tn�~(1/2)n�{�c)
�@�@�@�@ ��
�@�@�@�����i�P�^�Q�j���~[���Elog�i�v�|���{�Qi�j�{�b]
�@�@�@ �@��=1
�@���i�P�^�Q�j���b���b�@������A
�@�@�@�@�@ ��
�@�d�t������[�i�P�^�Q�j���~log�i�v�|���{�Qi�j]�{�b�@�@�E�E�E(3)
�@�@�@�@�@ ��=1
�@����A���̐l���q���ɎQ�����Ȃ����̖����x��(2)�ŕ\�킳��邩��A(2)�̒l��(3)�̒l�����������A�Q�������̒l�͌����ł���Ƃ�����B
�����ŁA(2)��(3)�����Ƃ����āAk�Ƃb����������ƁA
�@log�v����(�P�^�Q)i�Elog(�v�|���{�Q���j�@�@�E�E�E(4)
���Y�z�v��1000�S�~�i���\���~�j�Ƃ���ƁA
�@log�P�O3����(�P�^�Q)i�Elog(�P�O�O�O�|���{�Q���j
�������ƁA�����U�@�@�i�U�O�O�~�j�ɂȂ�B�y�G�N�Z�����g�����Ƃߕ��z���̎��ŋ��߂���A��P�P�i�P�P�O�O�~�j�ɂȂ����B
S�F�قƂ�ǂ̐l�̒������ʂƓ������Ȃ�ˁB�p���h�b�N�X�͏������킯���B
S�F�����l����ƁA(4)�̒l�͖����ɂȂ�Ȃ��̂ł��ˁB
T�F�x���k�[�C�͂���_�I���Ғl�ƌĂB����́A�u���Ҍ��p�v�̍ŏ��̕\�����ƌ����Ă���B
S�F���p���āH
T�F���p�Ƃ́A�l�����i���i��L���̃T�[�r�X�j������邱�Ƃ��瓾���閞���̐�����\�킷�B�x���k�[�C�́A�u���Y���̋��z�ł͂Ȃ��A���ꂪ�����炷�����̑����������I�ȍs����ɂƂ��ďd�v���v�Ƃ������Ƃ��ŏ��Ɍ������B��������~�N���o�ϊw���n�܂�B
S�F�ނ��낱����̕����s�v�c�ł��B���Ғl�i�̗��_�j��������������A�l�Ԃ̋��K���o���C������Ƃ������Ƃł����H
T�F�����ł��ˁB���Ғl���̂��͍̂l�����Ȃ��ŁA�l�Ԃ̊������i������������Ŕ������j�̕����C�������Ƃ����Ă��ǂ��B
S�F���̌v�Z�́A���w�ɐl�Ԃ����킹��̂ł͂Ȃ��l�Ԃ̊��o�ɐ��w�����킹���ƍl�����܂��ˁB
T�F����Ӗ��ł́u���w�̐l�ԉ��v�ł��ˁB�ł��A����͂�͂萔�w�̕��ɐl�Ԃ̊��o�����킹��u�l�Ԃ̗������v�̎��_�������ł��ˁB�����āA���̎��_���o�ϊw�ɓ�������邫���������Ƃ���ƁA��������āu���������ꂽ�����v���A�����I�ȍ������̒��ɑg�ݍ��܂�Ă����Ƃ����_�Ɂu�l�Ԃ̗������v���ؖ�����Ă���悤�ȋC�����܂��B
S�F�Ƃ���ŁA���̐l�̎����Ă�����Y�ɂ���Ė����x���ς��ƌ����Ă��A�P���~�̍w���͂́A���̐l�̍��Y�ɊW�Ȃ���������ˁB
S�F����ɁA�ŏ��ɂ����玝���Ă���̂��Ŋ��Ғl�i�����̎Q�����j���ς��Ȃ�ĕς���B
S�F���ꂩ�瓷���Ɠq����l�͈Ⴄ��B����ς���Ғl���̂��̂�����킯�ɂ͂����Ȃ��Ǝv���B
T�F��������ˁB�����ŁA���̊��Ғl�̕����C������l�����������l������B
�@W.�t�F���[(1893�`1990)�u�m���_�Ƃ��̉��p�v�Ƃ����l���B
�T�A�t�F���[�̉�@
T�F�ނ́A���̓q����W�{���o�Ƃ����m���_�̕����ɂ������B�����Ɏ��s�ł��Ȃ��l�Ԃ��q��������̂��A�W�{�ƍl�����̂��B���ʂ͕W�{�̑傫���������ɂ�āA�W�{���ϒl�͕�W�c���ϒl�ɋ߂Â��Ă����B
�@���̏ꍇ�A���Ғl�͕�W�c�̕��ϒl�ł���A�q���̎Q���҂����ۂɊl������܋��z�͕W�{�l�ł���B��������ƁA�W�{���ϒl�͂ǂ̂悤�ɂ��ĕ�W�c���ϒl�i���j�ɋ߂Â��Ă����̂��A�Q�����͂ǂ��ω�����̂����l�@�ł���B
�@���̂��Ƃ��ɂ���ăG�N�Z���Œ��ׂĂ݂悤�B
���s���P�O�̗ݏ�Ƃ��A�m�����l�̌ܓ����邱�Ƃŕ��z��\�킷�B���ۂɂ͂����͂����Ȃ����A�吔�̖@���ŗ��z�I�ȕ��z�ɋߊ���Ă����ƍl����B
��@���z�@�@�m���@�Q����10 100 1000 10000 100000 1000000 10000000
1�@ 200�@�@�@0.5�@�@�@�@�@ 5�@50�@500�@5000�@50000�@500000�@5000000
2�@ 400�@�@�@0.25�@�@�@�@�@3�@25�@250�@2500�@25000�@250000�@2500000
3�@ 800�@�@�@0.125�@�@�@�@ 1�@13�@125�@1250�@12500�@125000�@1250000
4 �@1600�@�@ 0.0625�@ �@�@ 1�@ 6�@ 63�@ 625�@ 6250�@ 62500�@ 625000
5 �@3200�@�@ 0.03125�@�@�@ 0�@ 3�@ 31�@ 313�@ 3125�@ 31250�@ 312500
6 �@6400�@�@ 0.015625�@�@�@0�@ 2�@ 16 �@156�@ 1563�@ 15625�@ 156250
7�@ 12800�@�@0.0078125�@�@ 0�@ 1�@�@8�@�@78�@�@781�@�@7813�@�@78125
8�@ 25600�@�@0.00390625�@�@0�@ 0�@�@4�@�@39�@�@391�@�@3906�@�@39063
9�@ 51200�@�@0.001953125�@ 0�@ 0�@�@2�@�@20�@�@195�@�@1953�@�@19531
10�@102400�@ 0.000976563�@ 0�@ 0�@�@1�@�@10�@�@ 98�@�@ 977�@�@ 9766
11�@204800 �@0.000488281�@ 0�@ 0�@�@0 �@�@5�@�@ 49�@�@ 488�@�@ 4883
12�@409600�@ 0.000244141�@ 0�@ 0�@�@0 �@�@2�@�@ 24�@�@ 244�@�@ 2441
13�@819200�@ 0.00012207�@�@0�@ 0�@�@0 �@�@1�@�@ 12�@�@ 122�@�@ 1221
14�@1638400�@6.10352E-05�@ 0�@ 0�@�@0 �@�@1�@�@�@6�@�@�@61�@�@�@610
15�@3276800�@3.05176E-05�@ 0�@ 0�@�@0 �@�@0�@�@�@3�@�@�@31�@�@�@305
16�@6553600�@1.52588E-05�@ 0�@ 0�@�@0 �@�@0�@�@�@2�@�@�@15�@�@�@153
17�@13107200 7.62939E-06�@ 0�@ 0�@�@0 �@�@0�@�@�@1�@�@�@ 8�@�@�@ 76
18�@26214400 3.8147E-06�@�@0�@ 0�@�@0 �@�@0�@�@�@0�@�@�@ 4�@�@�@ 38
19�@52428800 1.90735E-06�@ 0�@ 0�@�@0 �@�@0�@�@�@0�@�@�@ 2�@�@�@ 19
20�@104857600 9.53674E-07�@0�@ 0�@�@0 �@�@0�@�@�@0�@�@�@ 1�@�@�@ 10
21�@209715200 4.76837E-07�@0�@ 0�@�@0 �@�@0�@�@�@0�@�@�@ 0�@�@�@�@5
22�@419430400 2.38419E-07�@0�@ 0�@�@0 �@�@0�@�@�@0�@�@�@ 0�@�@�@�@2
23�@838860800 1.19209E-07�@0�@ 0�@�@0 �@�@0�@�@�@0�@�@�@ 0�@�@�@�@1
24�@1677721600 5.96046E-08 0�@ 0�@�@0�@�@ 0�@�@�@0�@�@�@ 0�@�@�@�@1
25�@3355443200 2.98023E-08 0�@ 0�@�@0�@�@ 0�@�@�@0�@�@�@ 0�@�@�@�@0
�@�@�@�@�@���Ғl�����ρ@ 460 752 1012�@1435�@ 1756�@�@2019�@�@ 2444
S�F�{���ɂ����Ȃ�́H
T�F����Ȃɂ��ꂢ�Ɍ��ʂ��o�邱�Ƃ͂Ȃ����낤���ǁA��̃��f���ɂ͂Ȃ�Ǝv���B
���������ƁA���Ғl�����������U���邱�Ƃ͗\���ł���B
�ł́A���̑������͂ǂ��Ȃ��Ă���̂��낤���B
�Ɗ��Ғl���������o���ƁA
�@��(��)�@�@ 10�@100�@1000�@10000�@100000�@1000000�@10000000
�@���Ғl�@�@�@460�@752�@1012 �@1435�@�@1756�@�@ 2019�@�@�@2444
�@100�Elog2�� 332�@664�@ 997�@ 1329�@�@1661�@�@ 1993�@�@�@2325
���̌����Ɗ��Ғl������I�Ȃ̂ŁA���Ғl�͉̑ΐ����ŕ\�킳��邱�Ƃ��\���ł���B
���ۂɂ����Бΐ��O���t�ɂ���Ƃقڒ����ɂȂ�B
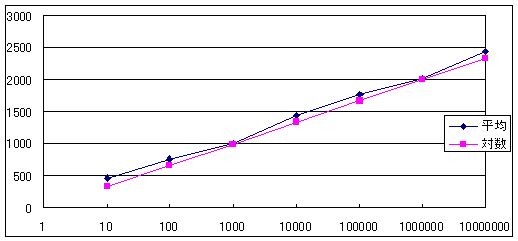
���������ƁA���Ғl�͂P�O�O�E������2���߂Â��Ă������Ƃ��\���ł���B
�܂Ƃ߂Ă݂悤�B
���̓q����Ɨ��ɂ���J�Ԃ��Ƃ���B�e��̊l���܋��z�͋��R�ɂ���ĕϓ����邩��m���ϐ��ƍl���āA�悋��ڂ̎��s�ɂ�����܋��z���wk�ŕ\�킷�ƁA
����̏܋��z�̑��v�́A�rn���w1�{�w2�{�E�E�E�{�wn
�Ƃ����m���ϐ��ŕ\�킳���B�i�\�̊��Ғl�́A�r���^���ŋ��߂Ă���j
�Ή����āA�Q����������̑��v���f n�Ƃ���B
���̂Ƃ������ȎQ�����́A�吔�̖@���ɂ��
�@�̓Á��O�ɑ��Ă������̂Ƃ�
�@�or�i�b�r���^�f���|�P�b���Áj���O�@�i�������j�@�E�E�E(5)
�����\���傫�����C�b�r���^�f���|�P�b���Âł���A
����͒ʏ�̐���̎����ŁA��@�r���^�f�����P�Ɏ������邱�Ƃ��Ӗ�����B
�b�r���^�f���|�P�b���ÂɂȂ�m�����O�ł���悤�Ȃf���͂ǂ����������낤���H
���́A��قǂ̕\�ƃO���t����A�f���^�����P�O�O�E������2���Ɨ\���ł���B
�t�F���[���ؖ������̂́A(5)��������f�������݂��C�����
�@�@�@�f���������Elog2���@�@ �@�i�����P�O�O�~�j�@�E�E�E(6)
�ł���Ƃ������Ƃ��B
���̂��Ƃ��t�F���[�̓`�F�r�V�F�t�̕s�������g���ďؖ������B
T�F����ŁA�����̌����ȎQ������������ɂȂ�̂́A���̓q������J�Ԃ��ꍇ�Ɍ���̂ł����āA�L����̂���Ԃ��ł͂��肦�Ȃ����Ƃ����������ƂɂȂ�B
S�F���Ғl���́A�����ׂ̖��Ǝv���Ă������ǁA���킷�邩�Ŋ��Ғl������Ă���Ƃ������ƂȂ̂ł��ˁB
S�F�ł́A���s�����܂��Ă��鎞�̋�̓I�Ȑ��l�͂ǂ��Ȃ��ł����H
T�F��̕\������킩��Ǝv�����ǁA�v�Z�ŏo�����Ƃ���A���Ғl�i���ώQ�����j�͂P�O�O�Elog2���ŋ��߂邱�Ƃ��ł���B
S�F�����Ȃ�ƁA����q�����s�����Ŋ|���������܂�킯������A������x�����I�ɍl���邱�Ƃ��ł���B
T�F�ł��A�𑽂�����ƎQ�����f�������܂�ɂ������Ȃ肷����̂ł��̓q������낤�Ƃ���l�͂��Ȃ��̂ł��B
S�F����ƃp���h�b�N�X���Ȃ��Ȃ�܂����ˁB
�y�Q�l�����z
�u����F�l�����Ă���K���v���O�����@������w�o�ʼn�@�˓c�����v�̒��̍��_�m��Y���̘_���u���p�ƓK�p�v���
�@�@�@�@�@�ڎ��ւ��ǂ�