 -------------------------
-------------------------【問題1】 左のような平行四辺形で、
?の角度を求めなさい。
-------------------------
T:これを解いたら、5をあげよう。
S:ホントに5をくれるの。
T:もちろん。期末テストが悪くてもこれを解いたといいうだけで5のねうちがある。
S:ヒントがほしいな。
T:これは補助線をいかに引くかの問題で、ポイントは正三角形と二等辺三角形です。
S:ヨーシ、やってみよう。
パズルから数学へ 数学からパズルへの誘い
――パズルは遊び。パズルは数学の母――
これは、一見簡単そうですが、やってみると案外と難しい問題です。まずはわかる角度をかきこみ、いろいろな補助線を引いて考えてみてください。
できなくとも、がっかりすることはありません。こういった問題は考えることに意味があるのです。そして、ギブアップしたら、答えを見て下さい。
S:えっ!答えを見てもいいの?
T:そうです。答えもヒント。パズルには一定の解き方パターンがあって、このパターンをつかめれば、同じような問題を解くことができるからね。
【ヒント】
AからDEに垂線を引きます。垂線の足をBとすると、なんと!!△ABCは正三角形になるのです。
【解答】
まず、∠CBDが30度になるようにBをとり二等辺三角形CDBを作ります。すると∠DCB=120度になります。つまり∠ACB=60度で、しかもDC=CA=CBすから、△ACBは正三角形になります。そうすると、CB=ABとなります。
さらに、∠ECB=15度からCB=BEがわかり、△ABEは二等辺三角形となって、∠AEB=45度となります。
このCBの補助線はなかなか思いつきませんよね。 図を見る
 さてそこで、この補助線の引き方の応用で、同じような問題を出します。
さてそこで、この補助線の引き方の応用で、同じような問題を出します。
--------------------------------------------
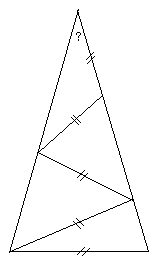
【問題2】頂角が20度の二等辺三角形で、左の図の
様に底角を60度と50度に分割する線があります。
?は何度でしょうか。
--------------------------------------------
S:これも補助線を引けばわかるの?
T:そうです。これも補助線を引いて正三角形を作ればいいのです。
S:まずわかっている角度を入れていくと・・・。
S:難しいよー。
これらの問題は、最初から正三角形と二等辺三角形からできている形(角度)であるという共通点があります。
もし、問題2が解けなかったら、こちらを先にやってみてください。大きなヒントです。
--------------------------------------------
【問題3】
右の図のような二等辺三角形はあるでしょうか?
あるとしたら、頂角は何度になるでしょうか?
--------------------------------------------
まず、頂角をχ°として、方程式を立ててみましょう。
どうですか。頂角はぴったり20度になるでしょう。そうすると、これを左の図に重ねることができます。さて、何がわかるでしょうか?
S:下から2番目の二等辺三角形は正三角形になるんじゃない。だって、底角が60°だよ。
S:そうすると・・。あっ、ここにも二等辺三角形がある。
S:わかった! ?は30°だ。
「図を見る」
この頂角が20度の二等辺三角形は、かなり[ユニークな二等辺三角形]です。二等辺三角形の中の二等辺三角形とでも言いましょうか。同様に問題1の平行四辺形は、二つの三角定規からできている平行四辺形です。平行四辺形のキングとでも言いましょうか。
2、問題づくり(逆に考える)・・・・意外性のある問題
--------------------------------------------------------------------------
【正多角形】
正多角形は全ての辺の長さと内角が同じ。
では、全ての辺と内角が同じ多角形は正多角形になるか?
ex.正六角形は内角が120度である。では、内角が100度の正多角形はどんな形か?
--------------------------------------------------------------------------
S:100度で作っていくと・・・あれ、辺と交わるところが100度ではないよ。正多角形にはならない。
T:そこで諦めない。それを続けて描いてみて。
S:線が交わってもいいの?
T:そう。でも辺の長さは同じにしてね。そうやっていくと、ぴったりと重なる時があるでしょう。
S:星型になるよ。
これは、「分数多角形」から考え出した問題です。一見できないように見えますが・・・。
ちなみに内角が90度なら、360÷(180−90)=4 となり、正四角形となります。
この考えでいくと、100度では、360÷(180−100)=9/2 となり、正9/2角形となるのですが・・・
この正多角形はどんな形になるのでしょうか? 【正9/2角形を見る】
何でも「逆」を考えるとより「一般化」できることがあります。こうやって正多角形を一般化することもできるのです。
S:一般化すると何か良いことがあるの?
T:そうだなぁ。世界が広がるというか。そうそう、発明なんかはこういう発想でやっている。「数の一般化」も応用の広いすばらしい発明だよ。
3、パズルにはパターンがある
私はパズルを解くことが苦手でした。自分は柔軟な思考ができないのだとコンプレックスを持っていました。ところが解答を見ると、なーんだと納得します。でも、どうやってこういう考え方ができたのだろうかと不思議でした。それ以来、すぐに解答を見るという方法をとってみました。すると、パズルの解き方には一定のパターンがあることがわかってきたのです。そしてそれはパズルの問題を作るパターンでもあったのです。
S:数学の問題自体がパズルのようなもんじゃない?
S:パズルだったら楽しんで解けるんだけどなぁ。
4、パズルをひろげる (パズルを楽しむ)
--------------------------------------------------------------------------
【チョコレートケーキの問題】 立方体のケーキがある。
このケーキにはチョコレートがかぶせてある。
このケーキをチョコレートの量も同じになるように3等分したい。どのように切ればいいか?
--------------------------------------------------------------------------
T:クリスマスのケーキを切るでしょう。もし丸くない正方形のチョコレートケーキならどう切るのかという問題。
S:底にはチョコレートがかかっていないんですね。
T:そうです。上と側面にチョコレートがかかっています。
S:横に3等分すると真ん中の人のチョコレートが少ないよ。
T:発想を少し変えてみて。直接3等分しなくてもいいんだよ。
S:わかった。9等分して3個ずつにすればいいんだ。
S:どう9等分するの?
S:辺を3等分して縦横を切れば、9等分になるよ。
S:だめだよ。かどが4つできるから3等分にはできない。
S:9等分がだめなら、12等分ならどう。
T:いいアイディアですね。ところでクリスマスケーキの場合はどうやって切っているの?
S:中心で等分すればできるかもしれない。三角形を作るんだ。
S:そうか、この三角形の高さと底辺が同じだから面積も同じだ。
S:ということは、チョコレートの量も同じになる。側面も同じだ。だから、これを4個ずつ集めれば3等分になる。できた!
T:よくできましたね。これは正方形を3等分するという問題だけど、側面にチョコレートがあるから等分の仕方に工夫がいる。じゃあ、正方形を長方形にしてもできるなかな?
「直方体のチョコレートケーキを3等分せよ」
S:正方形と同じようにできないのかな。
S:各辺を3等分して三角形を作ると、○の三角形と□の三角形の面積は同じなの?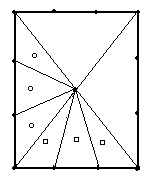
S:同じじゃないような気がするな。
S:同じだよ。だって、長方形を対角線で4つに切ったら、できた三角形は面積が等しいよ。
S:ちょっとまって。どうして面積が同じになるの?
S:長方形の対角線はお互いに等分するでしょ。これを底辺とすると高さが一緒だから面積が等しくなる。それを3等分するんだから一つの三角形の面積も等しくなる。○=□だ。
S:なるほど。
T:長方形にしても、正方形と同じことが成り立つんだね。これをパズルとして出す場合、長方形の方で出した方がより難しくなるね。辺の長さを3で割れるように指定するのも良いかもしれない。
5、パズルから数学へ
---------------------------------------------------------
【TとW】
Tに直線3本引いて三角形を5個つくるにはどうしたらいいか?
Wに直線を3本引いて三角形を9個作るにはどうしたらいいか?
---------------------------------------------------------
T:先生のホームページの掲示板にこういう問題を書いてきた人がいたんだ。Wの場合は8個までは見つけたんだけど9個ができない。誰か解いてみて。
S:先生もできなかったのか。私ならできるかもしれない。
S:Tの場合は「直線五本で三角形を5つ作れ」と同じことだね。
S:あれ、もしかしたら星型五角形は三角形が五つあるんじゃない。
T:「二分の五角形」は確かに5本で三角形が5つあるね。
S:できた。「図を見る」
T:渡辺くんができたみたいだから紹介するよ。どう?
S:間違いなく五個ある。
T:ではWの場合はどうだろう。Tを利用できないかな。
S:真ん中に星型五角形を作ったらどうだろう。
S:できた!「図を見る」
S:すごい。ちゃんと9個ある。
T:どうやらキーは星型五角形だったね。順番に調べてみようか。3本なら三角形は1つ。4本なら2つ。ところが5本だと一気に5つになる。調べてみてください。
S:6本だと7個かな。
S:表にしてみよう。7本を調べる人、8本を調べる人、9本を調べる人・・・
直線の本数: 3 4 5 6 7 8 9 10 ・・・
---------------------------------------------------
三角形の数: 1 2 5 7 11 15 21 ・・・
S:Wと3本で合計7本なのに、9個ではなく11個なのはどうして?
S:この表にはどういう法則があるんだろう?
T:先生も考えてみたけどわからなかった。この法則がわかったらすごい。「もしかしたら」と思いついたら教えてね。
T:その外にも疑問がいろいろと浮かんでくる。例えば、「五本の直線で一番三角形がたくさんできる形は星型五角形だけか」。それ以外にもあるのか。5個が最高か。もしそうなら、星型五角形は五本の直線で5個の三角形ができる図形と定義できる。面白い問題がいっぱい出てくるパズルだからぜひ研究してみてください。
リンク[パズルハウス]の「トライアングル」に挑戦!
------------------------------------------------------
【偽コインの問題】12個のコインの中に1個だけ偽物がある。
天秤を3回使ってその偽コインを見つけよ。
------------------------------------------------------
T:これは昔からある有名なパズルなんです。けっこう難しい。
S:重いか軽いかわかっていないんですね。
T:そうです。ポイントは本物と比べるといういことだね。
S:幾つに分ければいいのかな。二つに分けても意味がないし。
S:4,4,4と3つに分けて測ればいいんだ。もし釣り合えば残りの中にあるという事だからね。よし、やってみよう。
S:できないよ。何かヒントはないの。
T:例えば、2個の場合はできるかな。
S:2個だとどっちが偽物かわからないよ。3個だと2個が同じだから偽者はわかるけど。
S:3個だと2回測ればわかる。1個ずつ測って、もし傾いたら測らなかったのが本物だから、もう一回その本物と比べてみればいい。
T:じゃあ、4個だとどうだろう。
S:1,1,2と分けて、1と1を比べて釣り合ったら、残りの2個のうち1個と本物を比べる。もし釣りあわなかったら残りが本物だからそれとどちらか一方と比べる。つまり、2回でわかる。
T:5個だと何回でわかる?
S:2,2,1と分けて・・・。あれ?こんどは3回かかる。
T:どうやって測ったの?
S:釣り合ったら一回でわかる。釣り合わない時、●●(下がった方) ○○(上がった方) ◎(本物)と分かれるから、2回目は、●◎と●○で測る。もし釣り合えば、残りの○が偽物。もし、右が下がれば、右の●が偽物。もし、左が下がれば左の●か右の○だから、3回目にどちらかと本物を比べれば分かる。
S:なるほど。
T:●◎と●○で測るのがグッドアイディアだね。ではこの方法を使って6,7,8・・・と調べてみよう。
コインの数: 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17・・・
------------------------------------------------------------------
測る回数: 2 2 3 3 3 3 3 3 3 3 3 4 4 4 4・・・
S:3,3,3はできる。3,3,5もできる。最初に測るのは4,4までは3回でできるよ。残りのは5個までは3回でできる。4,4,6の6が4回かかる。3回でできるのは13個までだよ。
S:だったら、13個で3回という問題をだした方がいいのに。
S:12個の場合もいろいろなやり方があるね。【問題の解答】
T:4回まででできるのは何個までいくと思う?
---------------------------------------------------------------
【ユーロのお金の種類】
できるだけ少ない硬貨で、何通りもの金額を払うためには
どんな種類のお金を用意したらいいか。
例えば、100円までの金額を払うためには何種類のコインが何枚必要か?
---------------------------------------------------------------
こんな質問をうけました。
『来年(2002年)、ユーロ紙幣・通貨が発行されるそうです。紙幣は、5、10、20、50、100,200、500ユーロ。硬貨は、1、2、10、20、50セント、1、2ユーロ。
こんなに必要なのか? 計算する場合、偶数と奇数のお金は必要なのか? 日本では、紙幣1000、(2000、)5000、10000円。硬貨1、5、10,50、100、500円。
僕はコンビニに行ったときは、例えば、834円の商品は1034円のお金を出し、200円のおつりをもらうようにしている。525円だったら530円で5円のおつり。なるべくつり銭を貰わないように心がけています。やはり、1と5の組み合わせが妥当ではないでしょうか。ユーロが財布に入っていたら頭がパニックってしまうような気がします。』
いよいよヨーロッパの[グローバル化]が始まりましたね。これは面白い問題です。日本でも2000円札の発行がありましたが、あのお札はどこへ消えてしまったんでしょうね。2000円は必要ではなかったんでしょうか。
さて、1,5,10,50,100,500円が日本の硬貨です。2円硬貨や200円硬貨はありません。でも,私はユーロの方が便利だと思います。
ちなみに,ユーロだとたった2個のコインを使うだけで,50までで払える金額が18種類もあります。これが日本の硬貨だと9種類しかありません。3個だと34種類(日本の硬貨なら17種類)。お釣りを入れると,ほとんどの金額が3個のコインで足ります。日本のように1円玉が何個も財布の中にたまるという事はないのです。
例えば,34ユーロなら20ユーロと10ユーロと2ユーロを2個の計4個(枚)払えばいいのです。これが日本だと10円を3個と1円を4個の計7個(枚)です。
834なら,500と200と100と20と10と2と2を払います。500と500払えば,お釣りは50と10と5と1です。523なら,500と20と2と1ですから,引き算をしなくても出せるわけです。つまり,日本の硬貨の種類の少なさはお釣りを出すことを前提にしているわけです。引き算が苦手な人はユーロの方が良いですね。(わたしもそうです。)ユーロは硬貨が計算棒(器)のようなものになっています。
ちなみに一番少ない個数でどれだけまでの金額を払うことができるかというと,1,2,2,5,10,20,20の8個で110まではらうことができます。これが日本のお金なら1,1,1,1,5,10,10,10,10,50の10個で99円までです。
これは日本の硬貨とユーロの硬貨の比較になり、文化比較もできますね。ユーロは引き算を前提にせずに,お釣りなしで払うという発想ですね。
ここで、「100円までの全ての金額を払うことができる硬貨の一番少ない個数は?」
という問題ができます。かって,「天秤で重さを測るときにどんな錘がどれだけ必要か」という問題がありました。それと同じです。これは、2進法で考えるとわかり易い。1,2,4,8,16,32,64 の7個のお金で127までの全ての金額を払うことができます。このような金額のコインを作ったらきっと便利だと思うんですが・・・。これが最も合理的なコインのグローバル・スタンダードですよ。ユーロも円もどちらも十進法に規制されていますね。