ユニークな二等辺三角形
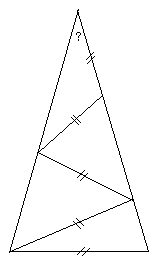
左の図の様に、二等辺三角形の中に二等辺三角形がある二等辺三角形の頂角は何度か？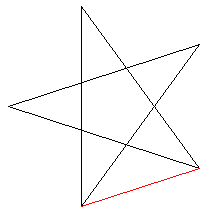
この三角形は、頂角をχとすると、底角は２χとなります。
５χ＝１８０ なので 頂角は３６度になります。
さて、この二等辺三角形はどんな性質を持っているでしょうか。
この二等辺三角形は、正５／２角形に出てくる形です。
この中には、二等辺三角形が２種類出てきます。頂角が３６°、１０８°の2種類です。
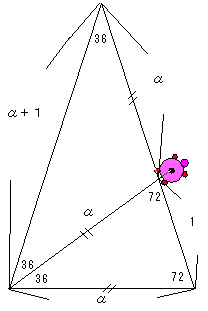
この二等辺三角形の底辺と斜辺は黄金分割になっています。
《図のように、小さい二等辺三角形の底辺の長さを１とし、斜辺（大きな二等辺三角形の底辺)をαとすると、 １：α＝α：（α＋１) で、α＾２＝α＋１ となり、α＝（１±√５）／２。（この図を黄金分割の定義にできますね。）》
つまり、この３６度は[黄金分割]を生み出す角度なんですね。
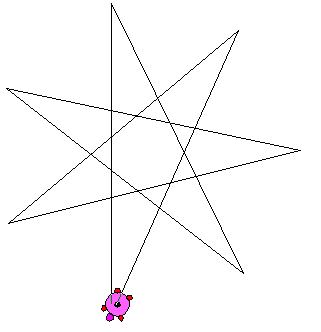
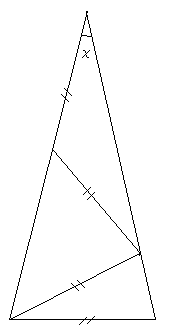
次は、二等辺三角形の中に二等辺三角形が３つある二等辺三角形です。
頂角は何度でしょうか？
頂角をχ°とすると、底角は３χ°になり、７χ＝１８０ で、頂角は１８０／７度になります。
これは、正７／３角形に出てくる二等辺三角形です。
これも面白い二等辺三角形です。
次は、二等辺三角形の中に二等辺三角形が４つある二等辺三角形です。
頂角は何度でしょうか？
頂角をχ°とすると、底角は４χ°になります。したがって、９χ＝１８０で
頂角は２０度になります。
これは、正９／４角形から出てきます。頂角にたいする外角が１６０°なので、
３６０／１６０＝９／４となります。
さて、この正多角形を見ると、いろいろな形が見えてきます。
下の図の中に角度を入れていくと、正三角形も見つかります。
また、下の右図のように線を引くと、「問題２」も見えてきます。
このように、二等辺三角形の中に相似な二等辺三角形を作っていくと、面白い問題がまだまだありそうです。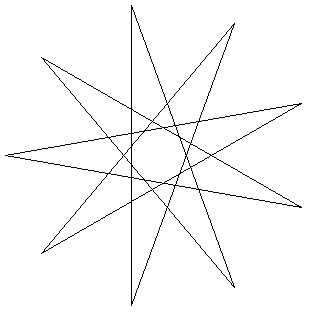
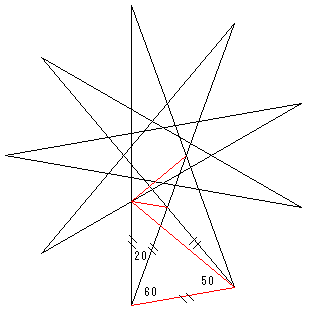
この場合正三角形ができるのは、６０度の時と２０度の時、さらに１２度の時です。