球の表面積の間違った求め方
S:球の表面積ってどうやって求めるのだろう。
S:円の場合は細かな三角形に分割して面積を求めたよ。円錐の側面積も三角形に分けると簡単に求めることがでる。球でも、同じじゃないかな。
S:そういえば、地球儀を作る時に細かな三角形を張り合わせるでしょう。
S:でも、球は表面が曲がっているよ。
S:大丈夫だよ。高さを球の大円で求めれば。
球の表面積
=底辺(円周)×高さ(円周の1/4)÷2×2
=2πr×1/4×2πr
=(πr)2
S:あれ? 4πr2 にはならない。どうして?
S:この値は何を示しているのかが気になる。
T:そういう場合は、実際に作ってみればどう。
S:隙すきですね。
T:そうですね。隙間が沢山あります。
S:展開図を見る限り隙間がなさそうなのになぜ
T:逆に球を展開してみよう。
S:曲がっているから平面にはならない。
S:でも、細かく切るとしたら、この三角形はほぼ平面になるのでは。
T:経線は展開すると直線だろうか?
S:わかった。経線は底辺と必ず直角になるから、三角形にはならない。
S:そうだ。三角形ではないから三角形の公式を使っても駄目なんだ。
T:じゃあ、(πr)2 と 4πr2 はどれだけ違うの?
S:π×πr2 と 4×πr2 を比べると、
S:π=3.141592…<4だから、すこし少ない。
S:その差、0.86πr2
S:これは、けっこう大きい。
S:球の体積からスイカの様に三角錐を作って表面積を求めるしかないのかな。
T:球面三角法で球面の三角形の面積を求める公式を使えばできるかも。
S:球面の三角形の面積=((球面上の三角形の内角の和−180)/720)×球の表面積 と出ていたよ。
S:赤道上では90度だから二角で180度。小さな三角形の頂点の角度の合計は360度。だから、(360/720)×球の表面積となってしまう。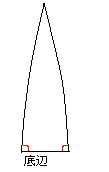
S:半球の表面積は(1/2)×表面積なんてあたりまえだ。
S:でも、最初の三角形の面積の公式が求まるよ。
2πr×πr/2×α=2πr2だから、α=2/π
最初の三角形の面積=2/π×底辺×高さ
=2/π×底辺×πr/2
=底辺×r
S:もしかしたら、この船のような形の面積がわかれば表面積を求めることができるのじゃない?
⇒【105、球の表面積と舟形多円錐図法】
目次へもどる
