舟形多円錐図法から球の表面積を求める
― 舟形はsinカーブだった！ ―
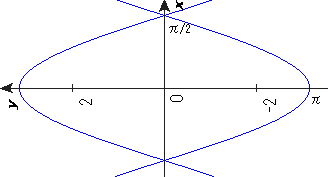
下図のような形で世界地図を描く方法を「舟形多円錐図法」というそうです。【１０２】
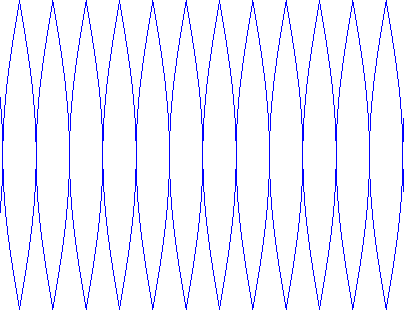
S：この船形の面積を求めることはできないのですか？
T：そういえば、昔、舟形を球に張り合わせて地球儀を作った覚えがあるよ。
S：もし、この船形の面積がわかれば、球の表面積を求めることができますね。
S：この船形の曲線はどんな曲線なの？
T：円の弧かな？ とにかく求めてみましょう。
S：船形の縦の曲線は大円。北極の角度をαとすれば、球の中心の角度もα。
S：この船形がどれだけふくらんでいるのかは、弧Lの長さがどう変わっていくのかを調べれば良い。
S：Ｌは上に上がっていくと小円になるね。小円は大円に対して常に90度だ。
S：そうすると、小円の弧は直線ではありませんね。
T：もともとこの船形はふくらんでいるので、平面にすることはできません。だけど、角度αをある程度小さくすれば平面に近くなります。
S：Ｌの長さは左下図の平行な小円の弧の長さだから、まず小円の半径Ｙを求めます。
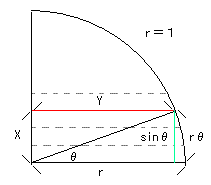Ｙ＝√（ｒ2−X2） （ピタゴラスの定理より）
Ｌ＝２π√（ｒ2−X2）×α／２π （角度はラジアン α／２π＝ａ／３６０）
＝√（ｒ2−X2）×α
仮に、α＝１とすると、
Ｌ＝√（ｒ2−X2）
T：これは、Xを変数としているので、大円の長さに変えないと駄目です。まず、ｒ＝１としましょう。
そうすると、Ｌ＝√（１−X2）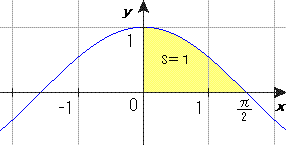
（ここからは高校レベルです） 弧の長さは角度θで表されます。X＝sinθだから、
Ｌ＝√（１−X2）＝√（１−sin2θ）
cos2θ＝1-sin2θなので、Ｌ＝cosθ
S：あれ？こんなに簡単になった。本当かな？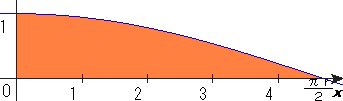
S：このθを拡大して、Ｌ＝cos（θ／ｒ）にすれば、半径ｒの舟形（右図）になります。
S：ということは、舟形多円錐図法はcos(sin)曲線だったということか。
T：では、ここから球の表面積を求めてみましょう。
S：この面積は求めることができるのですか？
T：cosカーブの面積は１とわかっています。
（∵∫cosθ・dθ[0≦θ≦π/2]＝[sinθ][0≦θ≦π/2]＝sinπ/2−sin0＝１）
横にｒ倍拡大すれば、面積は１×ｒ。下にもあるので、面積は２ｒ。
弧の長さは２。円周は２πｒだから、πｒ倍すると、２πｒ2が半球の面積となる。
S：ぴったりですね。cosカーブの船形は面積を正確に表しているようですね。
S：実際にcosカーブで半球を作ってみました。
前に作った三角形の時はすきすきだったけど、今度はしっかりと詰まっているようです。
T：サンソン図法という世界地図の描き方があって、これはcosカーブを使って、二つのcosカーブに囲まれた所の面積が半径１の球の表面積と同じになるように描いてあります。
S：前回三角形で表面積を求めようとして失敗したけれど、こうやって考えていくとけっこう奥が深いですね。
目次へもどる