%３ 【ピタゴラスの世界】
『第１話 ギターと音楽』
ここでは、ピタゴラスを紹介しよう。紀元前６世紀ごろの人。「世界は数（有理数）でできている」ということを主張した。そして、その証拠をいくつか上げている。その証拠の一つ。
図
（ギターを取り出し、曲を引く。）
――（拍手）
これはミ、では１オクターブ上のミはどこ？
（ギターを弾きながら、発問する。気持の良い一瞬である。）
――わからない。
実は、この弦のちょうど半分の所なのだ。この事を発見して１オクターブを八音階に分けたのがピタゴラスだ。そして、音楽も数学の原理にかなっていると主張した。音と音の周波数比ができるだけ小さな整数の比になっているという考えは、後に波動理論にもつながっていく。
この事がピタゴラスが数は万物のもとであると考えていた第一の理由。
第二の理由は、数で人生が説明できるということだ。
『第２話 愛と恋』
これから、ピタゴラスの世界観を説明します。きっと解らなくなるから、良く説明を聞いていて下さい。まず、１は理性を表す。２は女、３は男、４は正義または真理、５は結婚。６は恋愛、霊魂。７は何を示しているか解るね。
――幸福。その頃から、ラッキーセヴンがあったのか。
８は本質、愛。ピタゴラスは８を特別な数と考えたようです。さっきの、オクターブの発見から、８に対して愛着や、意味をもたせていたのだろう。９は色々調べてみたが解らなかった。１０は神聖な数。なんせ、１（最初の数）＋２（最初の偶数）＋３（最初の奇数）＋４（最初の平方数）＝１０なのだからだ。
さて、１＋２＝３だがこの式の意味する所は何か。
――女を馬鹿にしちゃいけないよ。
誤解の無いようにして欲しいのだが、これは僕の意見ではない。ピタゴラスの考えだからね。
２＋３＝５
これなんか簡単に解るね。当時、掛け算の方が足し算より高尚だと考えられていた。そこで、同じ事だが ２×３＝恋愛となる。
――結婚と恋愛は違うの。
古代ギリシャでは、恋愛と愛とは違う物だと考えられていた。恋愛は、動物的なもので、愛は人間だけが持つもの、だから恋愛より愛の方が優れている。
――でも、愛人は悪い意味で、恋人は良い意味に使われるんじゃない？
――（笑いながら）３＋３＝６はどう解釈するの？
当時は、さっきの恋愛と愛の違いと同じ理由で、男と女の愛よりも男同志の愛の方がより優れた愛だと考えられていた。だから、３＋３の方が２＋３より値打があると考えたわけだ。
――これは、ホモじゃないの。
いや、友情と考えた方がいいかもしれない。プラトンの本にそう書いてあるんだ。
ところで、昔の日本によく似たことも引出せる。たとえば、２＋５＝７ を訳すと、「女の幸せは結婚である」なんかは、昔の日本にも当てはまるよう内容だね。古代ギリシャと現代日本とそう変らないわけだ。
――私は、結婚が幸せだとは思わないよ。
――２＋２＋３＝７はどういう意味ですか。（男子はどっと笑う）
気持は分かるが、これを説明したら女の子から嫌われるからやらない。
ところで、この考え方は、人類が持った始めての体系的な世界観じゃないかなあ。
――数で人生を表わすなんて、確かに面白い考え方だなあ。
このようにピタゴラスは、世界は数で説明できるし、数からできていると考えていた。数に特別の意味があるものと考えていた。たとえば、６の約数は？
――２と３と６。
それだけ？
――あっ。１もそうだ。
そう、６はぬいてあとのを全て足してごらん。１＋２＋３＝？。
――６になる。
このように自分以外の約数を全て足すと自分自身になる数は大変珍しい。こういう数にピタゴラスは完全数と名前をつけた。完全数はまだある。６が一番小さい完全数だ。では次の完全数はいくつか？
――やってみよう。でも、だいたいいくつぐらい？
２０と３０の間にある。
――解った。
ピタゴラスが６を霊魂や恋愛としたのも、こういう意味からだろう。神様が６日間で全てのものを創ったという神話もここから来ているかもしれない。
参考文献 『数学セミナー１００人の数学者』 【比で世界を読み解く】
『第３話 点のあつまり』
万物が数でできているということの第３の理由は、線が点の集りだと考えていたことです。ピタゴラスは、原子論の考えを引きついたといってもいい。しかし、円に接する線は１点で接するというといったいどういう状態なのだろうか。
これを、図に表わそうと考えて、中学生の時ずいぶん悩んだことがある。
ピタゴラスはどうやらこう考えていたらしい。
図 ●●●●●●●●●●●
● ●
● ●
――この考えはどうもおかしいのではないの。だって、１点で接しているとは思えないよ。
確かにおかしいね。線を点の集りと考えることは無理がある。どんな偉い人にも間違いと言うのはあるもんだ。
――何か安心したな。
『第４話 三角数と四角数』
さて、ピタゴラスは一つ一つの数に個性（名前）を与えた。
図 三角数
１ ３ ６ 10
○ ○ ○ ○
○○ ○○ ○○
○○○ ○○○
○○○○
１ １＋２ １＋２＋３ １＋２＋３＋４
――２は「偶数」で、３は「奇数」なんていう呼び方の事ですね。
このように、一円玉を三角に並べる。
――あれ、一円玉がなんで黒板にひっつくの。
最近の一円玉は器用なんだ。ところで全部でいくつ。
――三個。
さらに一段つけたすと。
――六個。
こういうように三角形で表わされる数をピタゴラスは「三角数」と名づけた。では、さらに一段つけたすと。
――１０個。次は、１５個。
どういう計算をしたの。
――１０＋５＝１５
もっと詳しく。１０はどうやって出したの。
――１＋２＋３＋４＋５＝１５
つまり
――自然数の和。
三角数は自然数の和で表わすことができる。ここで問題。
１＋２＋３＋４＋・・・＋９＋１０はいくつ。
――知ってるよ。５５だ。
（ちなみに、どんな整数も３つの三角数の和として表せる：フェルマー・ガウス）
ピタゴラスは、これを三角数を利用して求めた。
――どうやって？
まず、同じ大きさの正方形を二つ合せて、一つの正方形に
正方形にしてみよう。これをジオジェブラで動かしてみよう。次をクリック！！
「ピタゴラスの定理」へ 「ピタゴラス＆ターレスの定理」へ
今見つけた法則は、ピタゴラスが発見して証明したといわれている。これをピタゴラスの定理（の逆）という。この命題を逆にすると、「直角三角形の直角をはさむ辺で作った２つの正方形の面積の和は、斜辺を辺とする正方形の面積に等しい。」という定理になる。この定理によって、長さを見つけることができたり、距離が解ったりする。数学史上で、最も大切で重要な定理なのだ。
――直角三角形の２辺が分かっていれば、あとの１辺は計算で出せる。
参考文献 遠山啓著『数学の広場、２次元の世界』ホルプ出版
『第７話 エジプトひも』
僕の友達に亀井喜久男さんという人がいる。彼の考案したひもを紹介しよう。昔、エジプトではナイル川の洪水で、土地の区画がたびたびわからなくなった。そこで再び土地の測量を始めなければならない。その時に活躍したのが、縄張師だ。彼等は縄を使って土地の測量をした。でも、どうやって縄を使っていたのかわかっていない。彼はどんな繩を使っていたのか考えた。その縄というのがこれだ。この縄は、輪になっていて１２に等分された印がついている。亀井先生はこの縄に、エジプトひもという名前を付けた。
――輪になっていたら、長い距離は測れないんじゃないの？
ところが、これが大変便利なんだ。たとえば、正三角形を作ってみよう。
――簡単さ。４ずつに分ければいいのさ。
――２等辺三角形も簡単に作れるよ。
できるね。では、ここに先生の作ったエジプトひもと釘がある。運動場に出て縄張師になり、色々な図形を作ろう。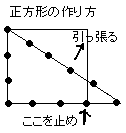
図 正方形の作図
今度は、正方形を作ってみよう。
――１２等分だから、１辺を３ずつにすればいいわけか。
いや、そう簡単には正方形にはならない。たとえば、菱形になる場合もある。
――角度を直角にしなければならないんだな。
――直角三角形を作るには、確か３：４：５だったから…３＋４＋５＝１２でぴったりになる。
――なるほど。それで１２等分か。
まず、３：４：５の直角三角形を作って９０度を作る。４の辺で３のところに印を打って５と１を合せた６の真ん中を引張ると、正方形ができる。では、長方形を作ってみよう。
――直角三角形から３の辺を２にして、引っ張ればいい。
次は、円を作ってみよう。
――丸くなんかできないよ。
このひもで円をつくらなくっても、地面に書くという方法もあるじゃないか。
――釘を使って。コンパスみたいに、使えばいいわけか。
楕円を作るにはどうしたらいいかわかるかい。
――楕円の中心は２つだから、釘を２本使って中心を固定し、円の時と同じようにピ
ンと引張ってずらしていけばいい。
図 楕円の作図
このエジプトひもで色々な図形を作ったり、応用することができる。たとえば、正六角形を作れる。野球のダイヤモンドも簡単に作れる。地面が水平であるかどうかもわかるし、日時計にもなるし、正確な南北もわかる。
このように、エジプトひもは大変便利なものだ。１２等分したところが、アイディアなんですね。
――１２というのは、１ダースだ。
――１２は約数が多い。１と２と３と４と６と１２の６個もある。
――１年も１２ヵ月。時計も１２時。
――十二支、十二宮にも使われている。何か意味があるのかな。
亀井先生の説によると、エジプト人が半日を１２時間に分けたのは、このひもを使っていたからではないかという。これらのことは、亀井先生の研究によるもので、彼はこのひもを教材用に商品化したんだ。
――へー、この縄は売れるの？
ある会社が売り出したいと言ってきたんだ。
『第８話 地球はどの位、曲っているか』
図 水平線は曲っている、それともまっすぐ？
水平線はどうなっている。
――丸くなっています。
なぜ？
――地球は丸いから。
でも、このまま曲っていたら、後に行ったら落ちこんじゃうだろ。
――あれ、おかしいな。
実は、先生も小学生の時、水平線は丸くなっていると思っていた。修学旅行で始めて海を見た時、真っ直ぐなのでびっくりした覚えがある。つまり、地球は丸いと聞いていてたから水平線も曲っていると思い込んでいたんだろう。この他にも、太陽の光線が雲の間から線になって照す時、平行なはずなのに広がって地上に届いているのも不思議だった。思い込みというのは、こういう間違いを起こすから、事実に即して考えたり、物を見たりすることは大事だね。
『富士山からどこまで見えるか。』
――あれ？地図なんか持ってきて、社会をやるの。
もちろん数学さ。日本で一番高い山は？
――富士山
何メートルか知ってる。
――３７７６ｍだったかな。
この富士山のてっぺんから遠くを眺めると、どこまで見えるだろうか。もちろん、雲一つない日本晴とする。
――琵琶湖が見える。
――四国が見える。
――九州まで見える。
――中国大陸が見える。
これをピタゴラスの定理を使って求めることができるのだ。
――どこに直角三角形があるの。
表面だけを見ていては直角三角形は見つからない。地球の中心と富士山を結んでみよう。
見える範囲はどこまで。
――円と接するところまでだと思います。
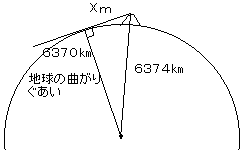
接線は中心と直角だから、直角三角形ができるね。地球の半径は６３７０㎞、富士山のたかさは４㎞として計算してみよう。
――斜辺が６３７４㎞と辺が６３７４㎞の直角三角形か。
――出た！ χ＝２２５．７８㎞。
――２２５㎞ということは、えーと。琵琶湖までしか見えないのか。
どうだい。地球の曲りぐあいは。思ったより大きいか小さいか。
――案外と曲がっていると思う。→【地球の曲がり具合を体験する（地球儀は数学がいっぱい)のページへ】
今は天気予報はひまわりの映像で、日本列島だけでなく地球の半分の写真を送ってくるけど、先生が中学生の頃、ひまわりはまだ飛んでいなかった。気象予報は、富士山レーダーの映像を写したものだった。できるだけ高いところにレーダー（カメラ）を取り付ければ遠いところまで見えるということで、日本で一番高いところにレーダーを設置するというアイデアを実行することになった。その困難な仕事をとりあげた石原裕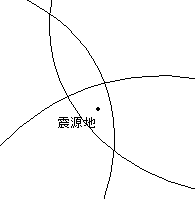
次郎の映画で有名になったのが、この富士山レーダーであった。
しかし、その映像は琵琶湖までしか写っていなかった。
――日本全部が写らなかったのか。
先日、消防署に勤めている教え子がきた。
≪田中君≫ 先生助けて。消防署の勉強会で地震のことをみんなに説明をしなければいけないけど、中学校の時に授業を聞いていなかったからもう一度教えて。震源の深さを求めるにはどうしたらいいの。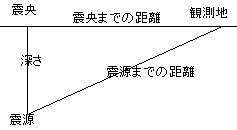
≪私≫ 久しぶりだな。ま、上がって。教科書を見せて。へー。震源の深さを求める時にピタゴラスの定理を使うのか。よしわかった。震源地を求めるにはｓ波とｐ波の時間の差は距離に比例するから、震源までの距離は求められる。震源地がわかったらピタゴラスの定理を使ってこの深さを求めるのだ。
≪田中君≫ピタゴラスの定理って何でしたか？
→【地震の研究（地球儀は数学がいっぱい)のページへ】
参考文献 『ピタゴラスからアインシュタインまで』K.O.フリードリックス著