エッシャーのように そのⅥ
ピタゴラスの定理の証明のしきつめ
0、しきつめは補助線
今までやってきたように、様々な図形をしきつめることができる。
そして、しきつめは一つの図形の時よりもずっと面白い形を生み出す。全体として見るからこそ、その図形の性質がより浮かび上がるのである。
ここでは、しきつめを使って、様々な定理の証明を考えてみよう。使ったソフトは、ペイント。同じ図をコピーしていった。
1、平行四辺形の性質と中点連結の定理
平行四辺形の性質は、全てこの三角形のしきつめの中にある。
対応する角や辺の長さが等しいこと、対角線が互いに二分することなど、このしきつめを見つめれば一目瞭然。
点対称と錯角同位角などの平行線の性質もわかる。さらに、真ん中の黄色い三角形を見ると、中点連結の定理も浮かび上がってくる。

2、ピタゴラスの定理
ピタゴラスの定理は、まず二つの正方形をどう並べるのかがポイントとなる。二つの正方形を並べてしきつめ、さらに斜線で正方形を作るとなると、並べ方は限られてくる。それは点対称で並べるしかない。
パズルのように、小と中の正方形を切り取った部品を並べなおすと、大の正方形になる。つまり、ピタゴラスの定理の証明になっている。
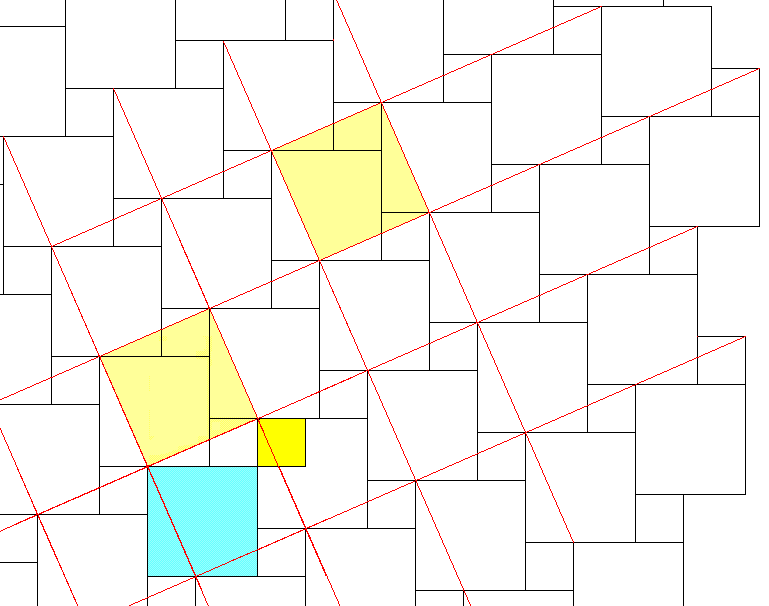
ピタゴラスの定理の図をそのまましきつめたらどうなるのだろうか。やってみた。不思議なことに、このように並ぶ。そして、このしきつめの中に、何通りかの証明が見えてくる。

これもしきつめられる証明。いや、証明をしきつめたもの。しかも、この図は右に傾いて見えるが、錯覚である。
薄緑の部分の面積は同じ。それが、小と中の正方形になっている。
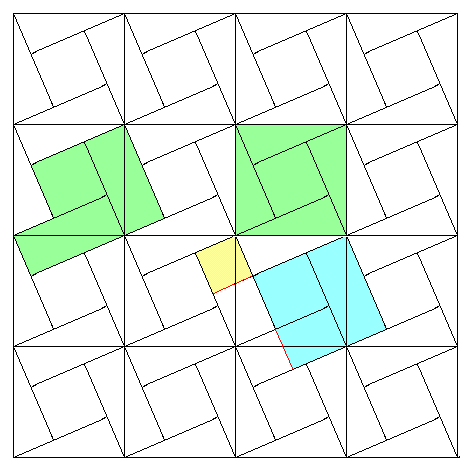
色々並べていて発見した極め付きの証明のしきつめ。ピタゴラスの定理をしきつめると、こんな図形になると、自信を持っていえる作品。美しい。
これも、何通りのもの証明が可能。しきつめていったときにできる隙間の部分も、いつも間にやら元の部分になっている所が見事。
3、四角形の面積
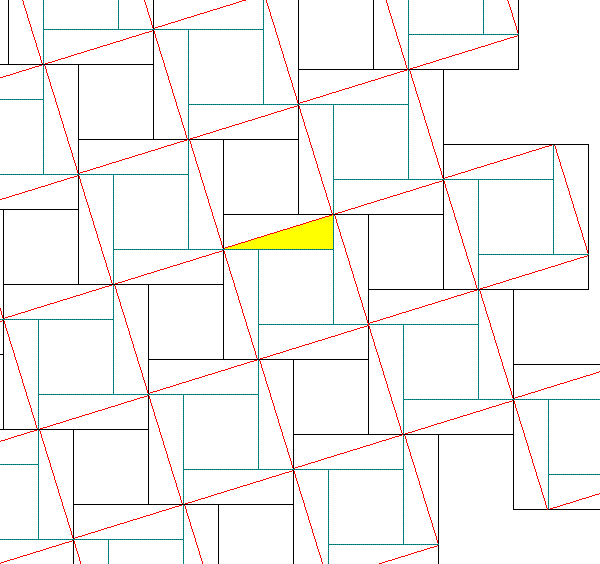
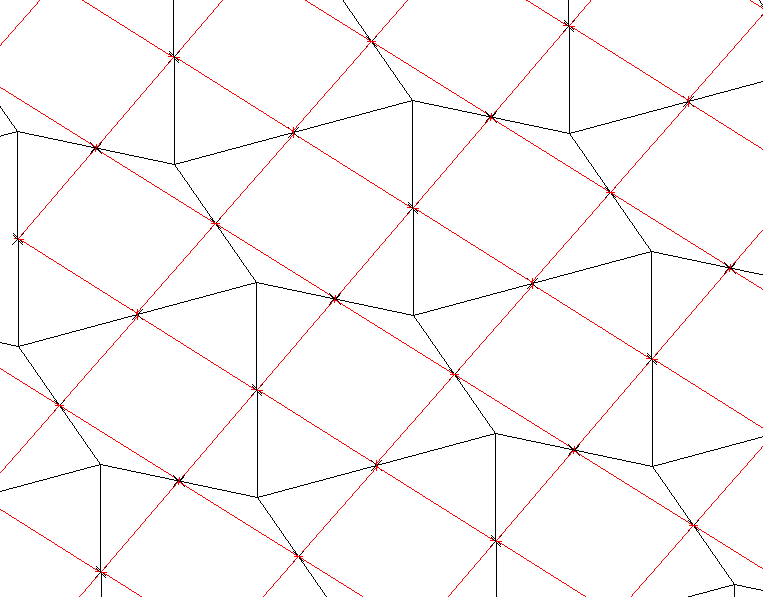
普通の四角形(黒い部分)の中点を図のように結ぶと、四角形が同じ面積の長方形(赤の部分)に変換する。
赤線で囲まれた長方形の面積と黒線の四角形の面積は同じである。
この長方形のしきつめには、ずれがある。では、長方形がずれないで並ぶ時はどんな四角形のときだろうか?
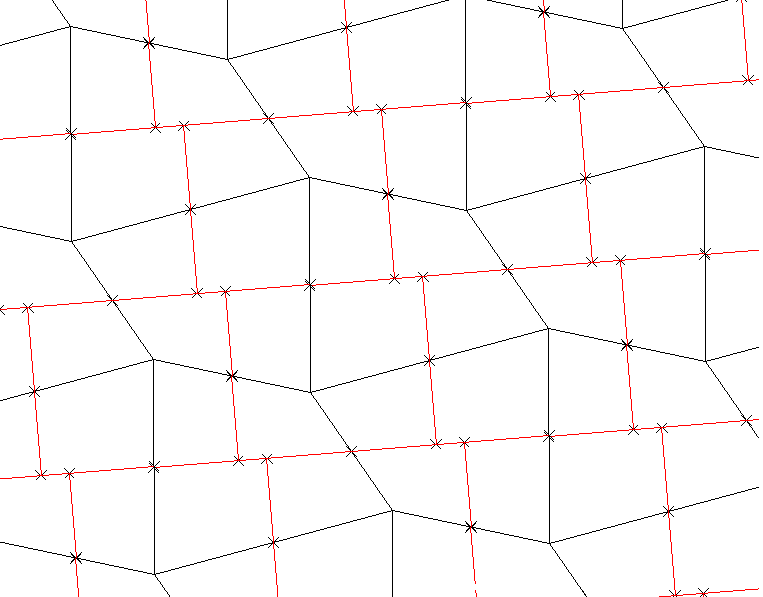
(→対角線の長さが同じとき)
4、四角形の中点連結
四角形の各辺の中点を結ぶと、どんな四角形でも必ず平行四辺形ができる。
ひし形になるのは、対角線が同じ長さのときである。では、この平行四辺形と四角形の面積の関係は?
(→平行四辺形の面積×2=四角形の面積)
と言うことは、平行四辺形の面積が求まれば、一般の四角形の面積は簡単に求まるということになる。
【四角形の面積を求める公式…検地の測量のしかた】
検地では、平行四辺形の対角線の長さ(四角形の中線の長さ)を求め、頂点から対角線への垂線の長さ(高さ)を求めれば、簡単に面積を計算できる。
四角形の面積=対角線の長さ×垂線の長さ×4
この図を、先の長方形の図に重ねてみると、もっとはっきりする。
5、内接四角形
この四角形は円に内接する四角形である。この内接四角形は、裏返しを入れると、このようにしきつめることができる。
作図するときの外心が残っていたので、何気なしに結んでみた。意外なことに外心を結ぶと、直角二等辺三角形と二等辺三角形ができる。なぜだろうか。
まだまだ何か出てきそうである。
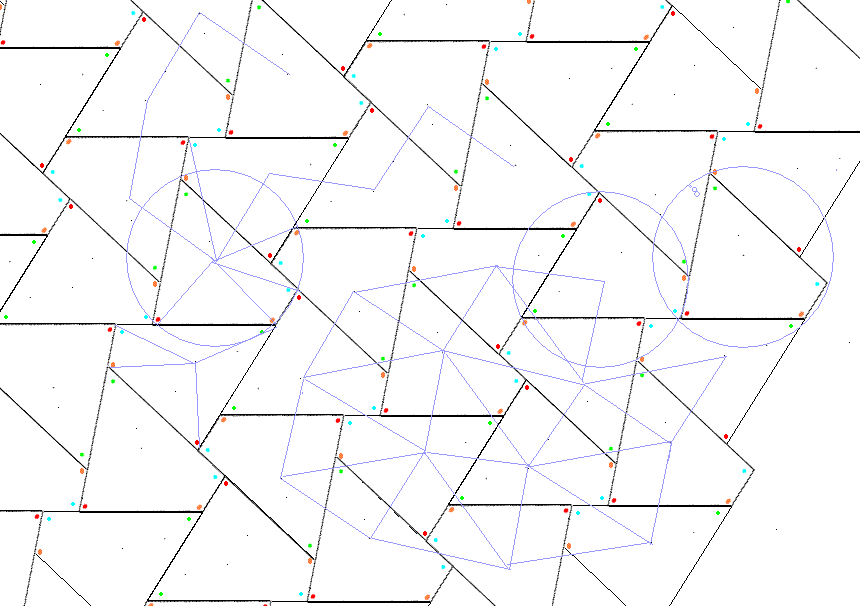
このように、しきつめをすることで図形の新たな性質も浮かび上がってくる。そして、美的な模様としてもけっこういけるのではないだろうか。
目次へもどる