美濃・飛騨の国の和算の歴史
算額の問題に挑戦しよう
１、澤田吾一先生のこと
「岐阜県の生んだ代表的な数学者は？」と聞かれれば、高木貞治先生（１８７５〜１９６０）と澤田吾一先生（１８６１〜１９３１）をあげることができます。
類体論や「解析概論」の高木貞治先生のことはよく知られていますが、澤田吾一先生のことあまり知られていません。しかし、是非知っていただきたい数学者です。
まず、以前紹介したサイトのページです。
１３、ありの巣から奈良時代の人口まで
『一つのアリの巣の中にアリは何匹いるか 奈良時代の人口は？』(1991.3)
さらに、先生の生涯を詳しく書いてある文章もあります。
この文章には、先生の生まれを滋賀県と書いてありますが、岐阜県の間違いです。
【92号澤田吾一 「二つの人生」】
（ワードファイル）この作者新井宏氏ご自身もとてもユニークな方です。
今回は、澤田先生の数学教育と和算についての著書を紹介します。いずれもネットで読むことができます。
両方を兼ねた著書として
『日本数学史講話』
という本を紹介します。
この本は、『奈良朝時代の民政・経済の数的研究』の数学史版ともいうべきもので、調査した正倉院文書などから考察した
奈良・平安時代の数学についても述べてあります。
また、講話という点がユニークで、文章は古いけれど内容は新しいものです。
その中で、「和算の歴史において、円理（円周や面積を求める理論、積分なども）
を一般に広めた功績は、大名の有馬氏と、僧侶忍澄に帰す」と澤田先生が書いています。
関流の秘伝を伝えられるためには、先師に対する誓約が必要でした。
そのことが、円理を一般民衆に広げることを妨げていたともいえます。
澤田先生は、大名と僧侶という世間から外れた人たちなので、その誓約に縛られなかった。
それが円理の世間一般への公開となり、和算の発展に大きく寄与したのであると書いています。（『日本数学史講話』より）
そして、初学者への説明としての公開の教育的功績は忍澄にあるとしています。
忍澄は美濃の人で海津郡吉里村鹿野緑林寺住職でした。
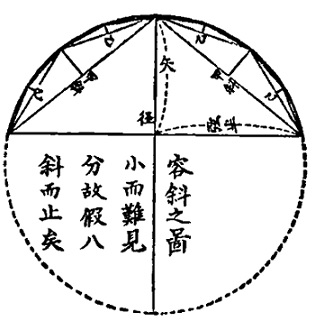
忍澄の著書は「圓理眞術・弧矢弦叩底（こしげんこうてい）」といい、初学者にもわかり易い内容となっています。
その内容は、径と弦を使って弧を求める術、径と弦を与えて矢（弓形の高さ）を求める術、
径弦を以て積を求める術、径と矢を与えて弦を求める術等が説明してあり、
しかもその術がどうして考えられたのかという起源をきちんと説明しています。
術を書いて、さらに術の起源を書いているのです。
和算には術だけが書いてあって、証明（説明）がないと言われていますが、この書は説明が実に懇切丁寧なのです。
ここに初めて算学を学ぶ人にとって絶好の教科書ができ、教育としての和算が誕生したのです。
２、和算の教育における意味
ところで、和算を取り上げた場合に、ナショナリズムと結びついた論調があります。
このことについて、以前から気になっていました。
それは「偏狭なナショナリズム」と結びつき、日本は素晴らしいと誇ることが他の国の人々を貶めることに利用される傾向があることです。
例えば、最近の出版業界に次のような傾向がみられると聞きました。
・「嫌中憎韓」をテーマにすると売れるという傾向
・「日本は素晴らしい論」も売れる
・若者の間に「右翼的な」傾向が広まっている
江戸時代の和算は世界に誇れるのものだったということは事実だと思います。
しかし、だから日本は素晴らしく特別なんだと考え、逆に周りの国々を貶めるという思考に飲み込まれるなら悲しいことです。
天元術は中国で生まれ、朝鮮半島から日本列島へ伝わり、この列島で深く研究されました。
和算はこの列島で独自に生み出されたのではなく、その種は大陸から伝わってきたのです。
では、どのように、どうして独自の発展をとげたのでしょうか。
「塵劫記」は、江戸期を通じてベストセラーの本になりました。
そして、中国から伝わった
天元術（高次方程式を解く方法）
を解読します。
その天元術を記録するために必然的に生み出されたのが点竄術です。
未知数を文字で表したり、公式を表す工夫をしています。
これは、記号を用いた代数学です。
そして、前章の様に出版や算額、塾を通じて庶民の中に広まってきました。
江戸時代のこの列島の人々は数学を、俳句をひねるように愛好しました。
和算の歴史的な意味を考えるとき、私たちはどうしても数学全体の歴史から和算を位置づけようとします。
だから、同時代のニュートンやガウスやガロアと対応する人物（関孝和など）を探してしまいます。
でも、この列島の現代と比べたらどうなのでしょうか。
「１＋１＝２は真理ではなく点数になっている。」というのが現在の学校の現場の状況です。
明治維新では、国（富国強兵）のため、立身出世のための数学になり、
それまでの中国から学んでいた文物を、今度は欧米から取り入れるようになりました。
それまで各学校や塾では何千という多様な教科書が使われていましたが、一つに統一されてしまいました。
そして、この列島の伝統の和算は明治維新であっさり滅び、
数学は子どもたちから優秀な人材を選別する道具になり、差別さえ生み出すようになってしまったと感じます。
教室で子どもたちがよく言っていました。
「わけはいいからやり方（答）を教えてほしい」
「結局合っているのか間違っているのかどちらなの？」
「これはテストに出るの？」
そして、
点数を１点でも上げるためにテストを持ってくる子たちを意欲的だとは思えませんでした。
私たちは子どもたちを苦しませ、数学嫌いを生み出したのです。
これに対して、この列島で和算を楽しんだ人たちを見ると、
年齢ではなく、点数ではなく、問題を解くこと、自身の学業が進歩すること、
新しい真理を発見することを、多様な学び方で楽しんでいました。
羨ましいかぎりです。
３、和算を支えた人たち
算額を見ると、子どもたちや女性の取り組んだ算題が書いてあります。
彼らは点数を上げるために算学に取り組んだのではありません。
算学の面白さにひかれたのです。
ここに大垣市の赤坂町明星輪寺にある「浅野孝光門人奉納算額」を紹介します。
全部で１２題の算題が美しく描かれ、そのうち１０題までは、答えと算題の順番を対応させるという楽しい工夫がなされています。
算題を考えたり解いた人の中に女性が３名います。その中に数えの１６歳
（行年とは数えで生まれてから今までの娑婆での修行の年数。亡くなった年ではありません）の少女がいます。
三ノ段の河合澤さんです。楕円と円の算題です。答えは、黄径＝青径÷３とわかっています。では、解けるでしょうか。
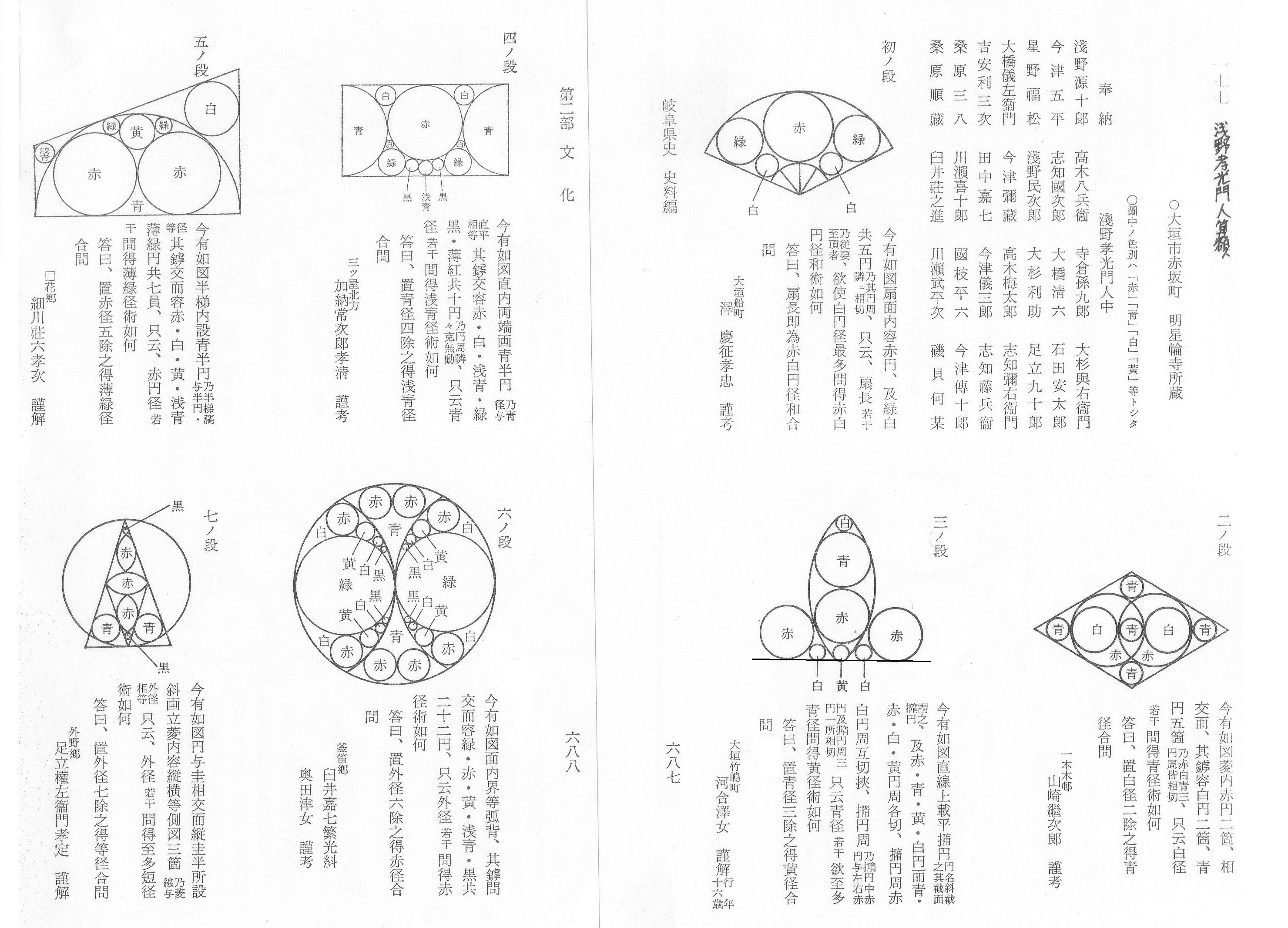ここでは六ノ段の奥田律さんの算題に取り組んでみましょう。中学生でも十分に解けます。
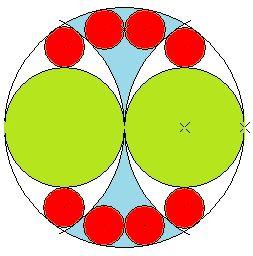問い
左上図のように接している円が２２個ある。
外径が与えられている時、赤の径を求める方法は？
答え
赤の径＝外径÷６
そもそもこの赤円の大きさは等しいのでしょうか。
そこで、白色側と水色側の場合に分けて考えます。
ピタゴラスの定理を使えば、すぐに６が求まります。簡単でしかもきれいです。
他の円は求めるのに関係ありませんが、こうやって並べるときれいですね。
このように数学を愛好する女性が複数いたことが、「どうして算学がこの列島に広まったのか」という理由を示していると思います。
同様に、小学生ぐらいの少年も大人と一緒に数学を学んでいました。
養老町高田の田代神社には１１、１２、１３歳の少年の解いた算題が描かれています。
『江戸時代の１１歳の少年の出した問題を解いてみよう』
世界的な業績をあげた有名な和算家もいますが、
注目すべきはこの様な少年や女性もが取り組んでいて、平等に算額に名を書き連ねているところです。
もちろん、算額には書かれてはいないけれど、算学に取り組んだ無数の人々が日本中にいたのです。
「和算が世界に誇るべきものだとしたら、それは市井の人々が算学を支えたことにある。」
「庶民から大名まで、天才からはほど遠い多くの無名の人々が算学を愛した。」
このことが、世界の中で特別な数学を生み出したといえるもとだったのです。
そして、それこそが最も大切なことなのではないでしょうか。
改めて強調しますが、それは明治維新と（ ）でこの列島から滅ぼされてしまったのだと思えてしまいます。
４、郡上八幡神社の算額現代語訳
少し難しいのですが、郡上八幡神社の算額を味わってみましょう。なお「円の径」とは、半径でなくすべて直径です。
第１問
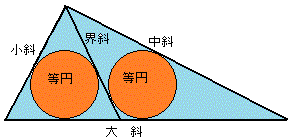「図のように三角形内に、界斜を隔てて二等円を入れる。中斜は２５７寸、小斜は６８寸、界斜は４０寸である。
大斜はいくつになるか？」
大・中・小斜と界斜の間にきれいな関係があります。
「答えて曰く。大斜３１５寸。」
「術に曰く。中斜に小斜を加え、これを自乗（２乗）し而して得た数を、界斜の冪（２乗）の４段（４倍）で減じて、
それを平方開（平方根）すれば問いに合う大斜を得る。」
つまり、大斜＝ √((中斜＋小斜)２−４×界斜２)
とてもきれいな公式です。問題は具体的数値ですが、「解き方＝術」は公式を求めているのです。
【解き方】
第２問
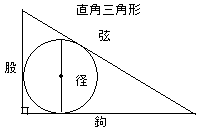「直角三角形に内接する円があり、鉤＋股＝１７。（鉤３＋股３＋径３）÷（弦−径）＝２１３。
弦の長さはどれだけか？」
「答えて曰く。弦は１３寸」
「術に曰く。只云数の自乗之を３の内に置き、又云数の２段（２倍）を減。
その平方開の商を以て只云数の２段を減ずと、余りが問いに合う弦である。」
つまり、弦＝２×１７−√（３×１７２−２１３×２）
３次方程式ができますが、それを２次方程式に直すことができます。
和算家は高次方程式を割り算して次数を下げていました。天元術も同様です。
【解き方】
右 神谷直縄 （『岐阜県の算額』に僧認澄と書いてありました。忍澄との関連はどうなのでしょうか）
第３問
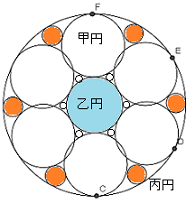「今、円の中に甲乙丙丁の１９の円を入れてある。丙は９.９寸。丁は２.９７寸。 大円の外径はいくつか？」（丁は一番小さい円）
「答えて曰く。外円の径は１００寸」（有奇＝余りが出る）
「術に曰く。角＝２√３＋４．５ 元＝（角×丙−(角−２)×丁）／(丙＋丁) 《勝手ながら術文の元を変更する》
外円の径＝｛元＋√[元２＋４(角−１)×丁／(丙＋丁)]｝×丙」
計算が大変です。でも、和算家の証明は計算でした。計算＝実験＝証明といっても良いのかもしれません。
第４問
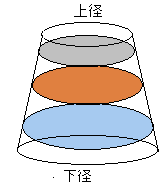「また、円台の内に三個の矮立円（回転楕円体）がぴったり入っている。矮立円の短径は等しい。
ただし、円台の上径の５分の３と下径の３分の２を合わせると15.41寸である。矮立円外の円錐台の体積が最小になる時の円錐台下径を得る術を問う。」
（３／５）×上径＋（２／３）×下径＝１５．４１
「答えて曰く。下径は１３.１２５寸」
いろいろ試したが、術文から答を導くことができなかったので計算によって求めると、上径が11.1のとき最小。
下径＝15.41×1.5−0.9×11.1＝13.125
最小問題です。まず、楕円体の体積を引かなければなりません。
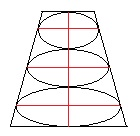楕円体の体積を求めるためには楕円体の長径を求めなければなりません。
下図のように楕円体の長径は少しずれています。どうやって求めたのでしょうか。
上径＝２ｖ，下径＝２ｕ，高さ＝ｈとすると、
長径２＝上底×下底 円錐台の体積＝π(ｖ２＋ｕ２＋ｕｖ)ｈ／３
であることはわかっています。楕円体の体積＝4π/3･(長径/2)2･ｈ/6
円錐台の体積−３つの楕円体の体積は、ｕかｖに関する二次方程式になります。
この問題を最初に解いたときに、答えが間違っていると思っていました。
しかし、それは問題の読み間違いでした。その結果、これは力のある人の算題であり、
浅野孝光（浅野孝光・天極斎。大垣の人、大垣に門人の算額あり。「岐阜県の算額の解説」より）にたどり着きました。
「ところが、大乗寺の高橋先生にお聞きしたところ、宮川は八幡町の紙屋五平治であり、神谷は郡上藩の藩士とわかりました。
【宮川孟弼についての調査とわかったこと】
（’15年6月加筆）」
右 宮川孟弼 （紙屋五平治、美濃八幡町の人）
関流 越中州 富山之人 高木允胤門人 某等 敬白
（高木充胤師は富山から高山や郡上へ出張して和算を教えていたと思われる。
中田高寛は越中富山桜井町で算学塾を開き関流直系五伝を名のった。越中における関流算学の開祖。
藤田貞資―中田高寛―高木廣當―高木充胤と続く。
高木充胤は能州（能登）方面で弟子が多い。
当時は、和算を教えに数か月の出張をすることもあったという。
飛騨の算額にも名がある。）
５、キツネザルとラーメンと和算と仏教
キツネザルはアフリカ大陸から渡ってきた数匹のサルがマダガスカルで進化し、
現在は１９種を数えるまでになったと言われています。元はひとつがいであった可能性もあります。
化石を発掘すると、すでに滅んだ種もあるようですから、
そのひとつがいから分化・進化し、多様な種を生み出したと想像されます。
ラーメンも大陸から麺が日本列島へ渡り、列島の様々な地でその風土に合った多様な進化をとげ、
現在、私たちの舌を楽しませてくれています。
ラーメンだけでも、この列島の風土を推し量ることができます。
そして、その開発の苦労も推察することができます。
【差別と多様性と同一化】
和算も同様です。
大陸から伝わった算学の書を読み解き、それをさらに発展させた先人たちがいたのです。
そして、江戸の中期にも清からの宣教師の伝えた算学の書や暦法の書を積極的に受け入れていました。
和算は列島の各地で、中央からの知識を求めながらも、それぞれの土地やそこに住む人々の中に広がっていきます。
仏教も同じです。仏教の場合は伝わった書物だけでなく、実際に大陸へ学びに行っています。
そして、大陸から伝わってきた仏教は、この列島で鎌倉期に独自の仏教として花開きました。
これらの対比の中には、何か共通するモノ・コトが汲み取れそうです。
まず、マダガスカルも日本列島も大陸の辺境の島だということです。
島嶼であるという環境も大きな影響を与えていると思います。
さらに、辺境ということは、その環境は中央からははるかに遠く、知的な資源も伝わりにくい所です。
だから、中央の文物は貴重であって、とにかく少しでも取り入れようと努力します。
その為には、開放的な姿勢がないと受け入れることはできません。
そして、列島の中の各地の風土人物にあったそれぞれの特色を出します。
そのまま受け入れるだけでなく、少しでも発展させようという意図が認められます。
ある意味、非常に細かく深入りしすぎと言う面もありますが、
でも、それは決して孤立しているわけでも、本質から離れたものでもありません。
また、この構造は列島の中にもあります。中央に対する周辺です。
歴史はいつも周辺から変化してきました。
この列島の歴史は、周辺から中央へという絶え間のない活動だったのかもしれません。
でも、周辺が中央へ進出した時、それはやがて衰えて新たな勢力が生まれてきました。
この列島に住む一人として、いつも田舎に住んでいるということを忘れてはならないと思っています。
そして、田舎こそ新しいモノを生み出すことができるのだと。
参考文献
『和算の解法―美しい幾何の問題を解く楽しみ―』米山忠興著
『岐阜県の算額の解説』高木重之著
目次へもどる