頭ではなく身体で理解する
―天元術を術としてマスターするために―
１．「天地明察」
映画「天地明察」を見た。最初は、映画のエンターテインメント的な演出に戸惑い、史実でないところが気になった。
例えば、関孝和は浪人風に扱われ、算術教授の看板がかけられていたが、彼は甲府藩の家臣であり、後に幕臣になっている。さらに、山崎闇斎が暗殺されたのにはびっくりした。でも、時間がたつと、別の面が見えてきた。
その一つは、主人公が「北極出地」の観測に出た時の上司である笠野高史演じる建部伝内と、岸部一徳演じる伊藤重孝たちの厳しさと優しさである。
二人は北極星の高度を予測（計算）してから観測を命じ、互いにより近かったことを楽しそうに自慢しあう。それを見ていた主人公の算哲（岡田准一君）が何をやっているのか聞くと、やってみるかと尋ねる。もちろん算哲は同意し、同じように歩測から始める。初めての計算で彼が合っていると、「御明察！」と大きく評価するのである。
算哲の創った問題を正す時も、優しく指摘している。何よりも自分で問題を作ることが最もすばらしいことであると考えている。
さらに彼らは、算哲から関孝和の話を聞いて、はるか年下なのに弟子入りしたいと望む。彼らの学を求める真摯さと同時に、自然や人間に対する尊敬の思いがにじみ出ている。
彼らは、命令によって算哲を動かそうとは考えていない。やってみようと自然に誘い、さらに自らの夢をも語る。そこには権威を振りかざそうとする気持ちは微塵も見られない。
もう一つは、天元術は表計算と同じなんだと気がついたこと。現代風に言えば、エクセルを使って問題を解くようなものである。算哲が、算額の問題を解くために、紙を広げて算木を置き解き始める場面がある。１元ｎ次方程式を解くために天元術を使っているのだ。
算哲の岡田准一くんが、実に楽しそうに算木を並べていた。それを見ていると、私も天元術を理解したいと、初めて思うようになった。
ネットで調べてみると、やり方が説明してある。でも、意味が分からない。
そこで、実際にやってみることにした。さっそく表を作り、算木も５㎜の角材を切って色を付けた。実際に並べてみると疑問が次から次へと浮かんでくる。でも並べながら考えるとなぜかわかってくる。
私は頭で理解することはできない。だから身体で理解するしかない。でも、身体で理解するとドーパミンが出てくる。そして、その幸福感は数日続く。
２．天元術を術としてマスターする
（１）基本の計算
まず、かけ算と割り算を算木を使ってやってみよう。自分で並べてみれば簡単にわかるし、身につく。
（算盤のＡ４サイズ印刷用ワードファイル、マッチ棒で算木を作る）
○かけ算
１２３×４５＝５５３５ をやってみよう。
まず、計算しやすくするために、桁をずらす。[一]は５で、[Ｔ]は６である。４５×１の答えを一番下の段に置く。次は４５を一つ右にずらして、４５×２を暗算で行う。
筆算の場合は位の小さい方から計算するが、算木では位の大きい方から計算する。
どうだろう。慣れてくれば計算機と同じなる。どれだけ桁数が大きくなっても計算できるし、小数でも大丈夫だ。
○わり算
５５３５÷４５＝１２３ をやってみよう。
これも桁を移動させてわかりやすく計算する。
５５÷４５＝１・・・１０ １０３÷４５＝２・・・１３ １３５÷４５＝３・・・０
さらに、
○いろいろな計算を実際にやってみよう。
○割り切れないものもやってみよう。
これで基礎の計算をマスターできた。次は方程式を解くことに挑戦してみよう。
（２）一次方程式を解く
「米7万8千石を325人に等分すると、一人が得る量はどれ程か？」
ここで天元の一を立て一人が得る量となす（一人が得る量をχとする）。
３２５χ－７８０００＝０ （天元術では方程式はゼロになることが大前提である）
まず、算木を布いてみよう。（算木を置くことを布くという） 定数は実に入れ、χの係数は法に入れる。
マイナスは黒、プラスは赤の算木を使う。χを求めるためには、両辺を３２５で割ればよい。ここで、さっきの割り算を使う。χは商に書き込む。先の割り算と異なるところは、実が負になっているところであり、商と法のかけ算を実に加えることだけである。実が０になったので割り切れた。
この時、（３２５χ－７８０００）÷３２５と考えないで、（３２５χ－７８０００）÷（χ－商）と計算するところが天元術の工夫である。
３２５ .
χ－２４０ ）３２５χ－７８０００
３２５χ－７８０００
０
結果を式で書くと、３２５（χ－２４０）＝０ （少しややこしいが、こう考えると二次方程式に拡張できる）
つまり、商＝χ＝２４０である。
一次方程式が割り算で解けたので、同様に割り算を使って二次方程式も解けることが予想できる。
（３）二次方程式を解く
「長方形の面積が15歩で縦横の和が8寸であるとき、縦と横の長さはそれぞれ何程か？」
天元の一を立て縦となす（縦をχとする）。
－χ2＋８χ－１５＝０ 算木を布く。
それぞれの係数を表に布く。
次に、これを（χ－□）で割る。□は商。ここで商に入る数を予測する。
実は足りなかったら後から付け足せばよいのだが、ここでは一度にやってみる。
商に３を立てる。 χ＝３ つまり、χ－３で割る。
－χ＋５ .
－１×３＝－３ χ－３ ）－χ2＋８χ－１５
－χ2＋３χ .
法＝８－３＝５ ＋５χ－１５
５×３＝１５ ５χ－１５
実＝－１５＋１５＝０ ０
実が０になった。 －χ2＋８χ－１５＝（χ－３）（－χ＋５）＝０
よって、χ＝３と５が求まる。
（４）三次方程式を解く
三次方程式も同じように解けるのだろうか？
「χ3－６χ2＋１１χ－６＝０ となるχを求めよ」
χ2－４χ＋３ .
商に２を立ててみよう。 χ－２ ）χ3－６χ2＋１１χ－６
偶×２＝２ χ3－２χ2 .
廉＝２－６＝－４ －４χ2＋１１χ
－４×２＝－８ －４χ2＋ ８χ .
法＝１１－８＝３ ３χ－６
３×２＝６ ３χ－６
実＝－６＋６＝０ ０
ここで、実が０になったので、χ＝２が求まった。他の解は、χ2－４χ＋３を同様に解けば求まる。
つまり、天元術は割り算をしているのである。だから答えは商なのだ。
（５）商をどう立てるか
でも、正しい商をどうやって見つけたらいいのかという問題が出てくる。
正しくない商の場合は何度もやり直さなくてはならないのだろうか。
（３）の問題 －χ2＋８χ－１５＝０ で考えてみよう。
仮に、商に２を立ててみよう。 つまり、χ－２で割るということだ。
－χ＋６ .
－１×２＝－２ χ－２ ）－χ2＋８χ－１５
－χ2＋２χ .
法＝８－２＝６ ＋６χ－１５
６×２＝１２ ６χ－１２
実＝－１５＋１２＝－３ －３
これを式に直すと、－χ2＋８χ－１５＝（χ－２）（－χ＋６）－３＝０ である。
でも、これでは算木で表された方程式も－χ2＋６χ－３＝０ となり、まったく別の方程式（根）になってしまう。
そこで、廉×２＝－２を法に加える。
そのわけは、（－χ＋６）を（χ－２）で割らなければ、等値な方程式にならないからである。
－１ .
χ－２ ）－χ＋６
－χ＋２
４
そうすると、 －χ2＋８χ－１５＝（χ－２）（－（χ－２）＋４）－３
＝－（χ－２）2＋４（χ－２）－３＝０
χ－２＝Ｘ と置くと ＝－Ｘ2＋４Ｘ－３＝０
となって、等価な（根が２小さい）方程式ができ、足りない商１を置けば、実は０になる。
＝（Ｘ－１）（－Ｘ＋３）＝０
そして、先の２と１を足して３が求まる。もう一つの根も２＋３＝５となる。
天元術は、根の値が変わらないように方程式を変換していくのである。
でも、次から次へと疑問が出てくる。例えば、商の桁が２桁以上の場合にも使えるんだろうか。
（６）χ2＋４χ－２２１＝０ を解いてみよう
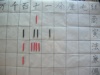
この場合は解は二ケタになる。そこでχ＝１０Ｘと置く。
この式は、１００Ｘ2＋４０Ｘ－２２１＝０ となる
表では廉を左に２つ、法を１つ移動させることになる。
１００Ｘ ＋１４０ .
Ｘ－１ ）１００Ｘ2＋ ４０Ｘ－２２１
１００Ｘ2－１００Ｘ .
１４０Ｘ－２２１
１４０Ｘ－１４０
－８１
これは、もちろん実が０にはならない。
式で書くと、１００Ｘ2＋４０Ｘ－２２１＝（Ｘ－１）（１００Ｘ＋１４０）－８１＝０である。
算木の係数で表現された方程式の値は０という約束があるので、新しい係数の方程式は、
１００Ｘ2＋１４０Ｘ－８１＝０ となって、根の違う方程式になってしまう。
ではどうしたらいいのだろうか。ここだけ注意が必要である。
ここで、(5)のように１００Ｘ＋１４０を再度（Ｘ－１）で割ってやるのである。
１００ .
Ｘ－１ ）１００Ｘ＋１４０
１００Ｘ－１００
２４０ （法の１４０が２４０になる！）
そうすると、１００Ｘ2＋４０Ｘ－２２１＝（Ｘ－１）（１００（Ｘ－１）＋２４０）－８１
＝１００（Ｘ－１）2＋２４０（Ｘ－１）－８１＝０
となり、新しい方程式ができる。（法の値が１４０ではなく、１００×１を足して２４０になる！）
この新しい方程式は十の位が求まっているので、一の位を求めるための方程式である。
そこで、Ｙ＝１０（Ｘ－１）と置く。
つまり、表の廉と法をもとの位置に戻す。
Ｙ2＋２４Ｙ－８１＝０ を解く。
商に３を立てる。３×廉を法にたす（２４＋３＝２７）。３×法を実にたす。
Ｙ ＋２７ .
Ｙ－３ ）Ｙ2＋２４Ｙ－８１
Ｙ2 －３Ｙ .
２７Ｙ－８１
２７Ｙ－８１
０
Ｙ2＋２４Ｙ－８１＝（Ｙ－３）（Ｙ＋２７）＝０
となり、χ＝１０＋３＝１３と１０－２７＝－１７が求まる。
（７）√２を求める
今までは、実が０になるようにやってきたが、実が０にならない時はどうなるのだろうか。
例えば、 χ2－２＝０ を解いてみよう。
商に１を立てる。
χ＋１ １ .
χ－１ ）χ2 －２ χ－１ ）χ＋１
χ2－χ χ－１
χ－２ ２
χ－１
－１
つまり、χ2－２＝（χ－１）（（χ－１）＋２）－１＝（χ－１）2＋２（χ－１）－１＝０
これで、一の位が求まった。
次に少数第一位を求める。
ｙ＝（χ－１）／１０ と置くと新しい方程式ができる。
ｙ2／１００＋２ｙ／１０－１＝０ なので、廉と法を右にそれぞれ２と１移動する。
１／１００×（ｙ2＋２０ｙ－１００）＝０と考えて解く。
商４を分に立てる。（５では実が正になってしまう）
ｙ ＋２４ １ .
ｙ－４ ）ｙ2＋２０ｙ－１００ ｙ－４ ）ｙ＋２４
ｙ2 －４ｙ ｙ －４
２４ｙ－１００ ２８
２４ｙ－ ９６
－４
ｙ2＋２０ｙ－１００＝（ｙ－４）（（ｙ－４）＋２８）－４＝（ｙ－４）2＋２８（ｙ－４）－４
これで、分の値が求まった。
次に厘を求める。
ｚ＝（ｙ－４）／１０と置いて新しい方程式を作る。
１／１００2×（ｚ2＋２８０ｚ－４００）＝０ を解く。商には１しか立たない。
以下同様に求めていくと、√２＝１．４１４２・・・と無限小数になる。
（８）２χ2＋３χ－３２４＝０ を天元術で解いてみよう
(9)２χ3＋５１χ2－１７３４χ＋９８２６＝０ を解いてみよう
これは、【１４０、１６２年前との対話 ・・・和算の問題に挑戦する】の問題である。
(10)算木の並び方はこれでいいの？
ここまで天元術をマスターした人は、映画「天地明察」の最初の算木の並び方がおかしいことに気がつくだろう。これは５次方程式になっている。でも、・・・
３．初手天元の意味
本因坊道策を相手に、主人公算哲が初手を天元を打つ場面が出てくる。
「天元の１を立てて未知数とする」というところから、初手天元の手が出てきたのだろう。ただし、この手で算哲は道策に負けている。
最後に、天元術は中国で考えられ日本に伝わった。それを理解し、さらに発展させて点竄術や円理などの和算を生み出した。貞享暦は中国の授時暦を経度の差を考慮して日本にあったように変えた。仏教も中国から伝わり、日本で独自の発展を遂げた。
私は以前ラーメンとキツネザルの譬でこのことを説明したことがあるが、日本という辺境は、特殊な進化を創り出すところかもしれない。そして、その中には世界にも通用するものがあると思っている。
参考サイト
【和算における方程式】愛知教育大学 内藤淳
【江戸時代のコンピュータ ～算木と算盤～ 錬成中学校 永井信一
目次へもどる