饽栚曇傒偱惓敧柺懱傪嶌傞
僆僀儔乕偺懡柺懱掕棟偺墳梡偵偍偗傞棟榑偲幚慔


T丗惓敧柺懱傪嶌偭偨偺偼慡偔棟榑偐傜丅
丂崱搙偼怑恖偑宱尡偐傜惗傒弌偟偨傕偺傪棟榑偐傜棤晅偗偰傒傛偆丅
丂埲慜丄捈曽懱傪嶌傠偆偲偟偰屲妏宍偩偗偱偼偱偒側偐偭偨丅
S丗屲妏宍偑侾俀屄昁梫側偺偱丄捀揰偑俉屄偱偼偆傑偔妱傟側偄偐傜偩偹丅
T丗偱傕丄偪傖傫偲怑恖偼嶌偭偰偄傞丅乮嫵偊偰偄偨偩偄偨價僨僆乯
丂怑恖偺曽偨偪偼饽栚曇傒偱捈曽懱傪偳偆傗偭偰嶌偭偰偄傞偺偩傠偆偐丅
S丗妋偐偵捈曽懱偵側偭偰偄傞丅
丂側傞傎偳丄屲妏宍偩偗偱側偔幍妏宍傪傕棙梡偡傞偺偐丅
S丗屲妏宍偲幍妏宍偱懪偪徚偟崌偭偰偄傞傫偠傖側偄偺丅
S丗偙傟偼僆僀儔乕偺懡柺懱掕棟偱棟榑壔偱偒傞両
侾侾俈丄僆僀儔乕偺懡柺懱掕棟偺巊偄曽丒丒丒幍妏宍偺晄巚媍丂丂乮俀侽侾侽丏係乯
S丗崱傑偱榋妏宍偲屲妏宍傪峫偊偰偒偨偗偳丄榋妏宍偼懪偪徚偟偰徚偊偰偟傑偆丅
丂乮俇倷乛俁亄倷亅俇倷乛俀亖侽丂偩偐傜乯
丂偲偡傞偲丄屲妏宍偲幍妏宍偩偗偱寁嶼偟偨傜偳偆側傞偐丅
屲妏宍偺悢傪倶丄幍妏宍偺悢傪倷偲偡傞丅
丂丂丂捀揰偺悢丂丂丂亄丂柺偺悢丂亅丂曈偺悢丂丂丂丂亖俀
丂乮俆倶亄俈倷乯乛俁亄乮倶亄倷乯亅乮俆倶亄俈倷乯乛俀亖俀
偙傟傪寁嶼偡傞偲丄
丂丂丂倶亅倷亖侾俀丂偲側傞丅
S丗偮傑傝丄屲妏宍偺悢亅幍妏宍偺悢偑侾俀偵側傟偽椙偄偺偩丅
S丗幚嵺偵偙偺饽偺價僨僆偱偼丄侾侽屄偺屲妏宍偲係屄偺幍妏宍傪嶌偭偰偄傞丅
S丗侾侽亅係亖俇
丂懡柺懱偺敿暘偩偐傜侾俀亐俀亖俇偱尒帠偵摉偰偼傑傞丅
S丗忋偺奧傕嶌偭偰偐傇偣傞偲丄
丂俀侽亅俉亖侾俀
T丗宱尡偐傜棟榑偵偁偰偼傔傞偙偲傕傑偨柺敀偄偹丅
嵍曈偺恾丅屲妏宍偑俆屄偱幍妏宍偑俀屄丅嵎偼俁屄丅斀懳懁傕摨條偵俁屄嵎丅
忋偺曈偺恾丅榋妏宍偩偗偱弌棃偰偄傞丅
丂柌拞偵側偭偰嶌偭偰偟傑偭偨丅
丂屻偼帩偮偲偙傠偺張棟丅
T丗偲偙傠偱丄偙偺捈曽懱偺饽偼怑恖偺曽偨偪偑宱尡偐傜嶌傝忋偘偰偒偨傕偺丅
丂偦偺宱尡傪棟榑壔偟偰傒傛偆丅
丂妏傪係偮偵偡傞偨傔偵偼嵍塃懳徧偱側偔偰偼側傜側偄丅
丂棟榑揑偵偼師偺恾偺傛偆側峔憿偑峫偊傜傟傞丅
丂偱傕偙偺恾偼偁偔傑偱摢偺拞偩偗偺傕偺丅
丂偩偐傜幚嵺偵偱偒傞偺偐妋偐傔偨偔側傞丅乮幚慔壔乯
S丗塃懁偺嵟彫偺捈曽懱傪嶌偭偰傒傛偆丅
丂杮摉偵偱偒傞偺偐丄偳傫側宍偵側傞偺偐丅昍偼偳偆宷偑偭偰偄傞偺偐丒丒丒丅
丂擇帪娫傎偳偐偗偰傛偆傗偔姰惉丅
恀忋偐傜尒傞丅
惓柺偐傜尒傞丅
恀墶偐傜尒傞乮懁柺乯
T丗棟榑偲幚慔偺偮側偑傝偑偄傠偄傠側妛傃傪憂傝弌偡傫偩丅
S丗怑恖偺饽偩偲懡柺懱偱偼側偄傛丅
T丗幚偼懡柺懱偵偟偨偺偼棟榑揑偵捛媮偟偨偐偭偨偐傜偱丄饽偱偼偙偺敿暘傪嶌傟偽椙偄偐傜偹丅
丂揝慄曇傒偼偙偺偡偒傑傪杽傔偰偄偗偽椙偄偲巚偆偗偳丄抾偱嶌傞帪偼偦偺曽朄偼晄壜擻偩偲嫵偊偰傕傜偭偨丅
T丗僆僀儔乕偺懡柺懱掕棟偺幃傪尒偰偄偨傜婥偑偮偄偨丅
崱傑偱榋妏宍乮饽栚曇傒乯傪婎杮偵峫偊偰偒偨偗偳丄巐妏宍偲嶰妏宍偩偭偨傜偳偆側傞偺偩傠偆偲丅
幃偱寁嶼偟偰傒傞丅
巐妏宍偵偡傞偲堜寘偵側傞偺偱捀揰偲廳側傞柺偼係屄偁傝丄
偟偨偑偭偰捀揰偺悢傪係偱妱傜側偗傟偽側傜側偄丅
巐妏宍偺悢傪倶丄嶰妏宍偺悢傪倷偲偡傞丅
乮係倶亄俁倷乯乛係亄乮倶亄倷乯亅乮係倶亄俁倷乯乛俀亖俀
係倶亄俁倷亄係倶亄係倷亅俉倶乕俇倷亖俉
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倷亖俉
巐妏宍偺悢偼偄偔偮偱傕傛偔丄嶰妏宍偺悢偑俉偩偲棫懱偵側傞丅
側傫偩丄偙傟偩偭偨傜掙柺偑係屄偩偐傜惓榋柺懱偑娙扨偵偱偒傞偺偱偼側偄偐
偲巚偄嶌偭偰傒偨丅
捀揰偑嶰妏宍偵側偭偰偄傞偙偲偑傢偐傞偩傠偆偐丅
乽偦偆偄偊偽抾饽偼掙柺偑係偐強愲偭偰偄偨側乿偲巚偄弌偟偨丅
偦偺棟桼偑僆僀儔乕偺懡柺懱掕棟偵傛偭偰愢柧偱偒偨丅
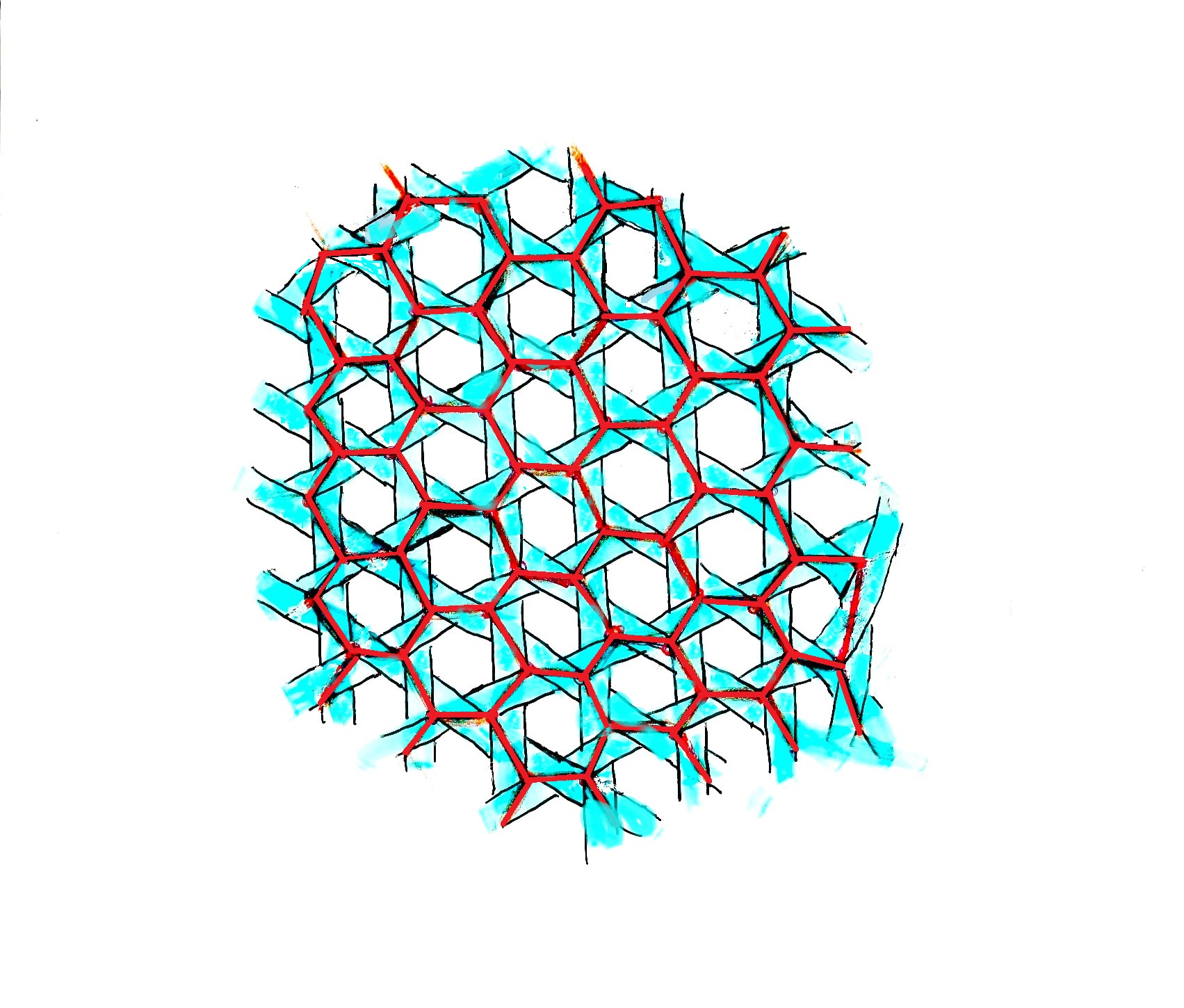
戝暘導/恀抾乮惵抾乯丂旽栚偐偛 | 庬椶偐傜扵偡,偐偛乮饽乯,偔偢偐偛 | 曢傜偟偺偐偛丒偞傞丒傒丂巗愳饽揦 (takekagoya.com)
偙偺偐偛偺嶌傝曽偼曽岦偑忋偺幨恀偲偼堎側傞丅偱傕忎晇偦偆偱崌棟揑丅
?