折りたたみの数学
― ダイヤカットからステント治療まで ―
１、ダイヤカット
T：もう１５年以上前のことだ。「ミウラ折り」を利用して作りたいものがあるけど、これは特許をとっているのかと質問をしてきた人がいた。
当時「ミウラ折り」のことを紹介していたのはこのサイトだけだったからだと思うが、返答に困った。
今では、折り紙を実用に利用することは当たり前のように様々な分野で行われている。
キリンの缶チューハイに、ダイヤカットがほどこされた缶がある。
三角形でできたひし形の模様が入っていて、プルトップを引っ張って開けたとたんに、ダイヤの折り目模様がきれいに浮かび上がる。
私は、「ミウラ折り」との連想で、これは空き缶をつぶしやすくするためのモノだと思っていたから、どのようにつぶれるのか試してみた。
ところが、つぶしにくいのだ。円筒よりもかえって丈夫になっていると感じた。
そこでインターネットで調べてみると、ダイヤカット（これを「吉村パターン」という）にした方がかえって強度が増すことがわかった。
→【チューハイ缶と宇宙研の関係】
《ダイヤカットは、缶を折りたたむのではなく、かえって強度が増す》
S：じゃあ、キリンはなぜ缶をダイヤカットにしたの？
S：強度が増すということは、材料が少なくてすむからもっと薄くできる。
だから、材料のコストが減って安くできる。
S：でも、作るときに大変だから、別のコストがかかるんじゃない。
S：きっと、見た目がきれいだからだよ。それで、評判になって売れるんだ。宣
伝効果をねらったんだ。
T：実際に作ってみよう。
S：どうやって作るの？
T：もちろん紙で作るのさ。折り紙はＯＲＩＧＡＭＩで通じる国際語だよ。
→【ダイヤカットの設計図：「キリンチューハイ氷結」の縮み】
S：面を曲げるほどダイヤが浮かび上がるね。
《曲面を曲げるほど、ひし形が浮かび上がる》
S：円筒よりもダイヤカットの方が丈夫ですよ。
S：きっと加わる力が分散されるからだ。
S：直線は曲線よりも強いということも大きな理由だよ。
T：では、今度は逆に柱を折りたたむにはどうしたら良いのだろうか？
S：ミウラ折りのような折り方があるんじゃないかな。
２、円柱を折りたたむ
T：どうやって折ったらいいのかを折り紙に聞いてみよう。
S：折り紙に聞くの？
T：実際に折りたためるのかどうかやってみるんですよ。
紙に聞いてみるというか、ねじ曲げる実験をしてみるんだ。
S：そんなことをしたら、紙がクシャクシャになってしまうよ。
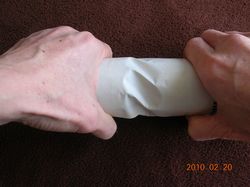
○ねじ曲げ実験
(1)まず、同じ直径の空き缶を用意して、丈夫な紙でへこんだ所を覆う。
(2)次に、この缶の周りに紙を巻く。缶と缶の間は少し開け。
(3)そして、ねじる。
(4)ねじったら缶どうしをしっかりと押さえつける。
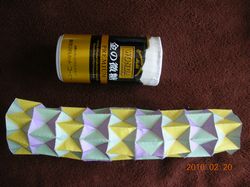
するとクシャクシャにならずに、写真のような跡ができる。
S：きれいですね。意外だなあ。
T：缶と缶の間の幅を変えながら何回もやってみよう。
S：三角形ができていますね。
S：なぜこのような三角形ができるのですか？
T：ねじった後に、片方だけ缶を取って底をのぞいてみよう。
S：きれいに折れていますね。
S：ねじった方向に紙が折れて角形ができているんだ。
T：さらに、この部分だけを切り取ってみよう。
S：真ん中の空白が大きいのと小さいのがありますね。
S：外側を見ると、多角形になっていますね。
S：折れ線は直線だから、円ではなく多角形になるんだ。
S：そして、ねじれた様な三角形ができる。
S：この多角形は正多角形かな。
T：この帯を開いてみるとどうなっているか？
S：ほとんど同じ形ですね。
○法則はないか
S：三角形の形に何か法則があるのかな。三角形の数は幅によって違う。
S：幅が大きくなると、三角形の数は少なくなるし、三角形は大きくなる。
S：同じ紙の三角形は合同なようだけど、違う紙のと比べると合同でもないし、相似でもない。
S：よし、三角形の角度も測ってみよう。
それぞれ角度が違うから、だいたいの値で求めるよ。
上の２０と書いてある所をα、右下の角をβとしよう。
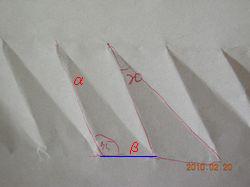○角度と三角形の数の関係
底辺の数 7 9 10 11 12
角α 20〜25 18〜20 17〜20 16〜18 15
角β 52〜57 45〜50 40〜42 39〜40 30〜32
S：もしかして、角αは１８０度を底辺の数で割ったものじゃないかな。
３、円筒折り紙構造
T：それ、すごい発見かもしれないよ。
よし、そのことを証明してみよう。
S：そんなことができるんですか？
○証明
T：まず、この帯を折りたたむことができたとしてみよう。
そうすると、きっと正多角形になるはず。
S：規則正しく折れたと考えるんですね。
T：そう。正ｎ角形に折りたためたとするとどうなるだろうか？
S：展開した図と折った図を比べてみるんですね。
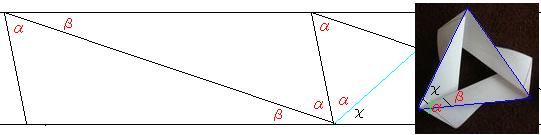
T：まず、上の図の角χを求めてみよう。
χ＝１８０−２α−β
一方、この正多角形の一つの内角を求めると、
内角＝１８０−３６０／ｎ
折った方の図を見ると、この内角からβを引くとχになる。
つまり、１８０−２α−β＝１８０−３６０／ｎ−β
βは消えて、
α＝１８０／ｎ となる。
《α＝１８０÷ｎ となるように三角形を作れば、折りたたむことができる》
S：これで、一段が折りたためることがわかった。
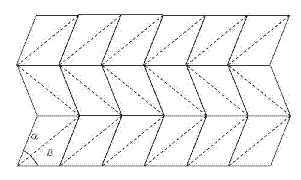
S：では、何段も重ねても折りたためることができるんだろうか？
○構造を作る
S：この折り方だと、外側の多角形の形は変わっていない。
同じ折り方でどんどん折っていくことができる。
S：つまり、何段あっても折りたためるということだ。
T：これを「円筒折り紙構造」という。
S：このｎ角形のｎをどんどん大きくしていけば、円筒に近くなるということか。
S：ところで、βの方はどうなっているの？
T：βの角度はαみたいには決まらない。
上の二つの三角柱のように、βを大きくすると真ん中の隙間が小さくなる。
そして、α＋β＝９０度のとき、隙間がなくなる。
だから、それ以上βを大きくすると折りたためなくなる。
S：上の四角形や六角形を見ると、上と下の多角形がずれていますね。でも、五角形はぴったりあっています。
T：実は五角形はα＝βにした。そうすると、ぴったり重なる。
S：上に積み上げる場合、交互に反転させる方法と同じ向きに積み上げる方法がありますね。
T：そうです。
では、左の二つの写真はどちらが同じ向きかわかる？
→【設計図A】 【設計図B】
○角柱を折りたたむ
S：α＋β＝９０の時は、角柱になりますね。
T：左の写真は正六角柱だ。これも折りたたむことができる。
設計図をのせておこう。
→【三角柱】 【六角柱】 黒線は山折り、赤線は谷折り
S：どちらも、１：２：√３三角定規が出てきます。三角定規をつないで折りたためる。
S：この方法を使うと、ペットボトルに折り跡をつけて、簡単に折りたたむことができますね。
T：実は折りたたむことができるということは、つぶせるということで、これを研究するということは、自動車を安全するために如何につぶすかという研究に結びつくという。
S：ということは折りたたみの研究は、私たちの安全をも護っているということか。
S：でも、これは、たたむのが難しいですね。もっと簡単にたためる方法はないのですか？
４、蛇腹折り
T：蛇腹折りというのがあります。昔、一眼のカメラに使われていた。
封筒を使って折ったもの。
この折り方は、六角形を作るように折っていく。
S：紙のリングを自然に折っていった時にできる折り方を、さっきと同様に積み重ねていったのですね。
これらは箱の折り方にも使われている。
○裏返しパズル
これまで考えてきた「折りたたみ」は、底の面と上の面があっても最後は重なる。
しかし、途中で変形するため、上の面は少し切り込みを入れなくてはいけない。
→【キュービックパズル】上から６〜８段目の立方体
(1)立方体を裏返しにできますか？
(2)立方体を平面に折りたためますか？
(3)牛乳パックを折りたたんで裏返しにできますか？
５、ステント治療
T：この折り紙技術を使って、動脈瘤をふさぐ手術に使った例がこれだ。
←
S：端っこを持って引っ張れば大きくなる。
S：小さくしてから血管に入れて、動脈瘤のところで、膨らませば、カテーテルで手術ができる。
S：でもどうやって膨らますのですか？
T：形状記憶合金と血管の流れの勢いで開くらしい。
このステントも折り紙を応用して、縦に折りたたむだけでなく円筒も小さく折りたためるようにしたものだ。
S：ミウラ折りだけじゃなくて、折り紙はいろいろなところで役立っているのですね。
→設計図【asｈiさんの部屋 折り紙ステントグラフト（人工血管 stentgraft)】へ
「折り紙を利用したステントグラフトの開発」栗林香織氏
参考文献【数学セミナー2009.１ 折り紙・折りたたみの数理】
◎宇宙ヨット「イカロス」
太陽風を受ける「イカロス」
の帆は１４メートル四方。
打ち上げのロケットにたたまれて
入れられ宇宙空間で広げられた。
その時に、
この折りたたみが利用されたらしい。
◎入れ物への利用
折りたたみできる牛乳パック入れ
ちゃんと利用されています。
きちんとたたみこむことができます。
使う時だけ組み立てます。
バレンタインデーでもらった
ゴディバのチョコレートケースに、
この折りたたみが使われていました。
プラスチックのケースを軽くねじると閉じます。
これは正方形ではなく、長方形にしてあります。
T：そもそも人は「生き物の折りたたみ」から学んでいるんだ。生き物はすでにこれらの折り方を利用しているよ。これは昆虫の翅の折りたたみ方。
【ハサミムシの翅の折りたたみ】
S：テントウムシの翅もきれいだね。
K：本当に凄い！自然界における動植物の進化発展は、神技ですね。
私も旅をして、自然が作り出した多くの造形物を見てきましたが、その造形美は人智の届かない領域にあるように思いました。
目次へもどる