乽嬌偲嬌慄乿擖栧
乗丂掕媊傪峀偘傞丂愙慄偐傜嬌慄傊丂乗
侾丆愙慄偐傜嬌慄傊
T丗偙偺懭墌偵愙慄傪堷偒傑偡丅傑偢俹傪摦偐偟偰傒傑偟傚偆丅
S丗摦偐偟偰偄偰傕壗傕尒偊偰偒傑偣傫丅
S丗偱傕丄擇偮偺愙揰偺娫偵壗偐娭學偑偁傝偦偆側婥偑偡傞丅愙揰傪寢傫偱傒傛偆丅
T丗偙偺慄傪堷偔偲尒偊偰偔傞儌僲偑偁傝傑偡偹丅偙偺慄傪俹偺嬌慄偲偄偄傑偡丅
S丗偳偆偟偰嬌慄偲偄偆偺偱偡偐丠
T丗俹傪嬌偲尵偄傑偡丅偦偺嬌偺嶌傞慄偩偐傜嬌慄偱偡丅
S丗俹偑奜偵偁傞帪偼愙慄偑堷偗傞偗偳丄恾偺拞偵擖傞偲愙慄偼柍偔側傞偐傜嬌慄傕柍偄偺偱偟傚偆偐丠
T丗偦傟偑崱擔偺妛廗偺戝帠側壽戣偱偡丅偦偺億僀儞僩偼乽掕媊傪峀偘傞偙偲乿偱偡丅偮傑傝丄俹偑懭墌偺撪晹偵擖偭偨帪傕嬌慄傪掕媊偱偒側偄偐偲偄偆偙偲偱偡丅
S丗俹偼捈慄忋偵抲偄偰偁傞丅傕偆堦偮暿偺揰俫偐傜愙慄傪堷偔偲丒丒丒
S丗尫乮嬌慄乯偺岎揰偼摦偐側偄傛丅偙偺揰俲偺堄枴偼壗偩傠偆丠
S丗傕偟偐偟偨傜丄偙偺俲偺嬌慄偑偙偺捈慄側偺偐側丅
S丗媡偵峫偊傞偲丄俲傪捠傞尫偺愙慄偺岎揰偼偙偺捈慄忋偵偁傞丅
S丗乽俹傪捠傞尫乿偭偰偳偆偄偆堄枴偱偡偐丠
T丗俹傪捠傞尫偼柍悢偵偁傝傑偡丅俻傪摦偐偡偲尫俻俼偑摦偒傑偡丅偦偟偰丄俻偲俼偺愙慄傪嶌恾偡傞偲丒丒丒晄巚媍側尰徾偑弌偰偔傞偺偱偡丅
S丗偁傟丄擇偮偺愙慄偺岎揰俽偼嬌慄偺忋偵偁傝傑偡傛丅偳偆偟偰偩傠偆丠
T丗晄巚媍偱偡偹丅徹柧偟偰傒傑偟傚偆丅
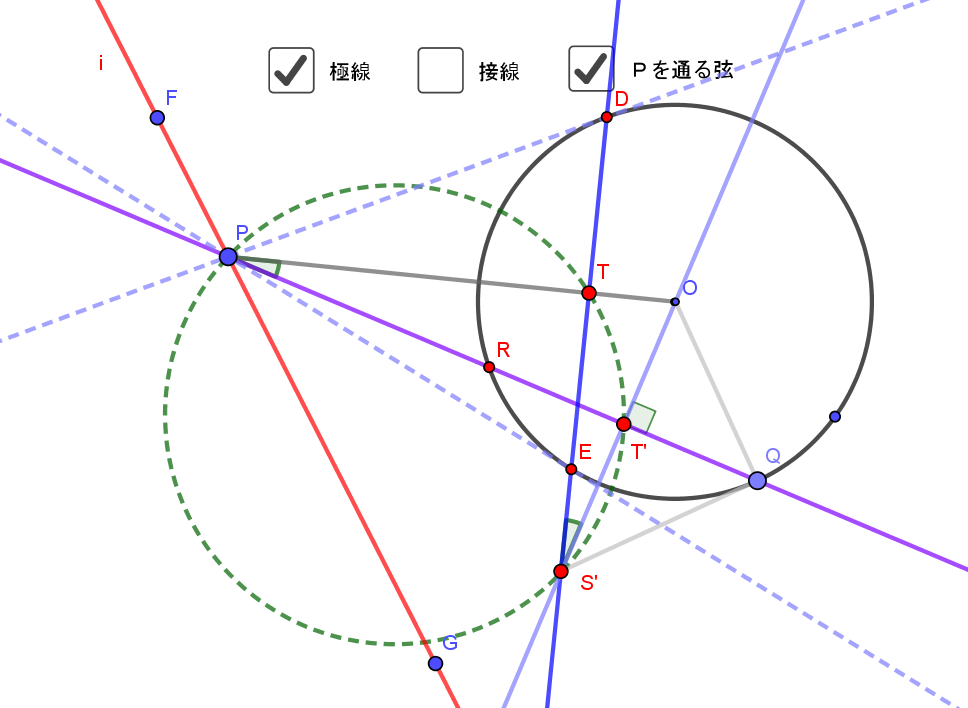 偨偩懭墌偱偼擄偟偄偺偱墌偱傗傝傑偡丅偙偺懭墌偺徟揰傪嬤偯偗偰墌偵偟偰傒傑偟傚偆丅僺僢僞儕偱側偔偰傕偄偄偱偡傛丅
偦偟偰墌偺拞怱俷偐傜俹俻偵悅慄傪堷偒傑偡丅
偦偺悅慄偲嬌慄俢俤偲偺岎揰傪俽'偲偟傑偡丅俷俹偲俢俤偲偺岎揰傪俿丄俷俽'偲俹俻偲偺岎揰傪俿'偲偟傑偡丅
偨偩懭墌偱偼擄偟偄偺偱墌偱傗傝傑偡丅偙偺懭墌偺徟揰傪嬤偯偗偰墌偵偟偰傒傑偟傚偆丅僺僢僞儕偱側偔偰傕偄偄偱偡傛丅
偦偟偰墌偺拞怱俷偐傜俹俻偵悅慄傪堷偒傑偡丅
偦偺悅慄偲嬌慄俢俤偲偺岎揰傪俽'偲偟傑偡丅俷俹偲俢俤偲偺岎揰傪俿丄俷俽'偲俹俻偲偺岎揰傪俿'偲偟傑偡丅
S丗偙偺俽'偲俽偑堦抳偡傟偽偄偄傫偩丅
S丗佢俿亖佢俿'亖佢俼偩偐傜墌偑昤偗傞丅
T丗偡傞偲丒丒丒
S丗仮俷俿'俹佷仮俷俿俽'偩丅憡帡斾傪媮傔傞偲俷俹丗俷俿'亖俷俽'丗俷俿丅
S丗偮傑傝丄俷俹丒俷俿亖俷俿'丒俷俽'亖倰2亖俷俻2丅偲偄偆偙偲偼丄俷俿'丗俷俻亖俷俻丗俷俽'丅
S丗傛偭偰仮俷俻俿'佷仮俷俽'俻偩偐傜乮堦妏偲斾偑憡摍乯丄佢俷俻俽'亖佢俷俿'俻亖佢俼丅
S丗偮傑傝俻俽'偼俻偺愙慄偩偐傜丄俽偲俽亴偼堦抳偡傞丅
T丗偙偺掕棟偺媡傪億儞僗儗偺掕棟偲尵偄傑偡丅
乽墌俷偵娭偡傞俹偺嬌慄傪俙俛偲偡傞偲偒丄俙俛忋偺堦揰俹'偺嬌慄偼俹傪捠傞乿偲偰傕戝帠側掕棟偱偡丅
佀亂億儞僗儗偺掕棟亃
S丗墌偩偲愙慄偺惈幙偐傜偐傜捈妏偵側傞偺偱俹傪捠傞傫偩丅偱傕墌偱偼惉傝棫偮偙偲偼傢偐偭偨偗偳丄偙傟偼懭墌偱偡傛丅
T丗墌偱惉傝棫偭偨恾傪僗儔僀僪偵偟偰幬傔偺暻偵塮偟傑偡丅偳傫側恾偵側傞偱偟傚偆偐丠
S丗宍偼曄傢傞偗偳捈慄偼捈慄偵側傞丅埵抲娭學偼曄傢傜側偄側丅偦偟偰墌偼懭墌偵側傝傑偡丅
S丗偮傑傝懭墌偱傕惉傝棫偮傢偗偩丅俽偺嬌慄偼俹傪捠傞丅
俀丆嬌慄傪偳偆掕媊偡傞偐
T丗偝偰丄崱搙偼俧傪摦偐偟偰丄俹傪懭墌偺拞偵擖傟偰傒傛偆丅
S丗愙慄偼徚偊傑偡偹丅偱傕丄尫偼堷偔偙偲偑偱偒傞偟丄俻偲俼偺愙慄偼堷偗傑偡丅
S丗俢傪摦偐偡偲丄偙偺愙慄偺岎揰偺婳愓偼捈慄傪昤偔丅偱傕偙偺捈慄傪偳偆傗偭偰嶌恾偟偨傜偄偄偺丠
T丗俹偺嬌慄偺嶌恾偺巇曽偼忋偺傾僀僐儞偺係斣栚乮悅慄乯傪僋儕僢僋偟偰俇斣栚乮嬌慄乯傪慖傃丄俹傪僋儕僢僋偟偰偐傜懭墌傪僋儕僢僋偡傟偽嶌恾偱偒傑偡丅
S丗側傫偩娙扨偵嶌恾偱偒傞傫偠傖側偄丅偳偆偟偰憗偔嫵偊偰偔傟側偐偭偨偺丅
S丗偙傟偱懭墌偺拞偵嬌偑偁傞帪偺嬌慄偑掕媊偱偒傞丅乽嬌俹偐傜懭墌偵尫傪堷偄偰丄俻偲俼偺愙慄偺岎揰偺嶌傞慄偑嬌慄丅乿
T丗偝偭偒俲偺嬌慄偑俥俧偵側傞傫偠傖側偄偐偲尵偭偰偄偨偗偳丄偦偺捠傝側傫偱偡偹丅
S丗崱傑偱偺帠偐傜乽嬌偑奜晹偵偁傟偽愙揰傪寢傫偩慄乿丅乽撪晹偵偁傟偽俹傪捠傞尫偺愙慄偺岎揰偺嶌傞慄乿丅
S丗偦傟偵丄億儞僗儗偺掕棟偵傛傝丄乽嬌慄忋偺揰偺嬌慄偼尦偺嬌傪捠傞乿亖乽嬌偺尫偺嶌傞愙慄偼嬌慄傪嶌傞乿丅
俁丆嬌慄偺惈幙
T丗崱搙偼嬌慄偺惈幙傪挷傋偰傒傑偟傚偆丅戝帠側惈幙偺堦偮偵撪暘丒奜暘偺娭學偑偁傝傑偡丅
S丗偙偺恾偱EG丗GF亖ED丗DF偲偄偆偙偲偱偡偹丅
T丗偙偺娭學偼師偺幃偱昞偡偲曋棙偱偡丅
\[
\frac{EG}{GF}丒\frac{DF}{ED}亖侾
\]
S丗嬌偲嬌慄偼恾宍傪撪暘偲奜暘偵暘偗傞傫偱偡偹丅
T丗偙偺恾偺俰偺堄枴偵偮偄偰偼亂嶰妏宍偺嬌偲嬌慄傊偺桿偄亃傊
係丆嬌慄偺柺敀偝
T丗曻暔慄偱傕嬌慄傪峫偊傞偙偲偑偱偒傑偡丅俥偑徟揰偱俠俢偼弨慄偱偡丅
S丗弨慄偲偄偆偺偼徟揰偺嬌慄側傫偱偡偹丅
S丗弨慄忋偺揰偐傜偺愙慄偼捈妏偠傖側偄丠
丒丒丒
S丗捈妏嶰妏宍偺幬曈偑弨慄偱擇摍暘偝傟偰偄傑偡偹丅
T丗嬌偲嬌慄偺惈幙偺傑偲傔傪彂偄偰偍偒傑偡丅
丂嘆丂乽儔丒僀乕儖偺掕棟乿
丂丂丂嬌俹偺嬌慄忋偺揰偺嬌慄偼俹傪捠傞丅
丂丂丂嬌慄偑俹傪捠傟偽丄偦偺嬌偼俹偺嬌慄忋偵偁傞丅
丂嘇丂嬌俙偺嬌慄忋傪揰俹偑摦偔帪丄俹偺嬌慄偼俙傪拞怱偵夞揮偡傞丅
丂嘊丂嬌慄偑堦揰偱岎傢傞帪丄偦偺嬌偼堦捈慄忋偵偁傞丅
丂嘋丂嬌傪捠傞墌悇嬋慄偺擇偮偺愙揰偼嬌慄忋偵偁傞丅
丂嘍丂揰偑帺恎偺嬌慄忋偵偁傞側傜丄偦偺揰偼墌悕嬋慄忋偵偁傞丅乮偮傑傝愙慄乯
丂嘐丂偳偺捈慄傕墌悕嬋慄偵懳偟偰嬌傪帩偮丅
S丗偙傟傜偼掕棟偲偟偰梡偄偰傕椙偄偺偱偡偹丅
T丗偦偆偱偡丅偙傟傜偼懱尡偟偰恎偵偮偗傞偲摉偨傝慜偵姶偠偰偒傑偡丅
GeoGebra偱偝傜偵怺偔挷傋偰傒傑偟傚偆丅
亂墌偺嬌偲嬌慄亃
亂墌偵奜愙偡傞懡妏宍偺嬌偲嬌慄 亃
亂嬌偲嬌慄偑帵偡墌偲嶰妏宍丒巐妏宍丒榋妏宍偺懳徧惈亃
丂丂丂丂丂栚師傊傕偳傞
 偨偩懭墌偱偼擄偟偄偺偱墌偱傗傝傑偡丅偙偺懭墌偺徟揰傪嬤偯偗偰墌偵偟偰傒傑偟傚偆丅僺僢僞儕偱側偔偰傕偄偄偱偡傛丅
偦偟偰墌偺拞怱俷偐傜俹俻偵悅慄傪堷偒傑偡丅
偦偺悅慄偲嬌慄俢俤偲偺岎揰傪俽'偲偟傑偡丅俷俹偲俢俤偲偺岎揰傪俿丄俷俽'偲俹俻偲偺岎揰傪俿'偲偟傑偡丅
偨偩懭墌偱偼擄偟偄偺偱墌偱傗傝傑偡丅偙偺懭墌偺徟揰傪嬤偯偗偰墌偵偟偰傒傑偟傚偆丅僺僢僞儕偱側偔偰傕偄偄偱偡傛丅
偦偟偰墌偺拞怱俷偐傜俹俻偵悅慄傪堷偒傑偡丅
偦偺悅慄偲嬌慄俢俤偲偺岎揰傪俽'偲偟傑偡丅俷俹偲俢俤偲偺岎揰傪俿丄俷俽'偲俹俻偲偺岎揰傪俿'偲偟傑偡丅