三角形の極と極線への誘い
－三角形の極線の性質から円錐曲線へ－
０、前もって
T：この学習をするにあたって【円の極線と円錐曲線の極線】についてと、次の定理を前提とします。それぞれ調べておいてください。
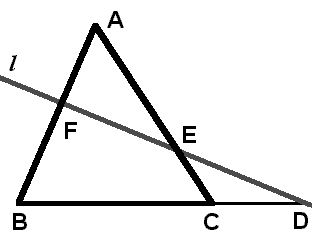〇メネラウスの定理
任意の直線lと三角形ABCにおいて、直線lとBC、CA、ABの交点をそれぞれD、E、Fとする。この時、次の等式が成立する。なお、直線ｌは三角形の外部にあってもよい。
\(
\frac{ＡＦ}{ＦＢ}\cdot\frac{ＢＤ}{ＤＣ}\cdot\frac{ＣＥ}{ＥＡ}=1\)
逆も成立し、この式が成り立てばＤＥＦは一直線上に並ぶ。
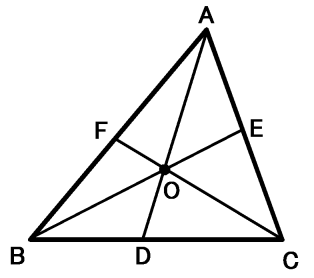〇チェバの定理
三角形ABCにおいて、三角形の内部に任意の点Oをとり、直線AOとBC、BOとCA、COとABの交点をそれぞれD、E、Fとする。
この時、次の等式が成立する。なお、点Oは、三角形の内部にあっても外部にあってもよい。
\(
\frac{ＡＦ}{ＦＢ}\cdot\frac{ＢＤ}{ＤＣ}\cdot\frac{ＣＥ}{ＥＡ}=1\)
逆も成立し、この式が成り立てば３直線は一点Ｏで交わる。
S：図は違うけど、式は両方とも同じだ。上が「一直線に並ぶ」で、下が「一点で交わる」の違いだ。
１、内分と外分
T：内分と外分は知ってるいるよね。
S：（内分）ＡＣ：ＣＢ＝１：２＝ＢＢ'：Ｂ'Ａ（外分）となる関係でしょ。
T：そうです。ではこれを作図することができますか？
S：この式からできないかな。そうだ。ＣＢをxとしてこの比を使うと、方程式が出来てxが求まる。
T：さすがですね。計算すればできますね。でもそれを作図で求めるにはどうしたら良いのでしょうか？
S：さっきの定理たちを使うんだと思うけど・・・。
T：そうです。下の図のように三角形を作ります。
S：これだけだと作図の順番がわからないな。
T：作図の手順は下のナビゲーションでわかります。ＤはどこでもＯＫ。余分な式や文字は、マウスを右クリックをすればメニューが出てきて消すことができます。
S：まずＤを動かしてみよう。
S：Ｄを動かしても、Ｂ'の位置は変わらない。Ｅを動かしてもＦＧはいつもＢ'を指し示している。
S：ところがＣを動かすとＢ'は変化する。
S：どうしてＢ'の位置が変わらないの？
２、なぜ変わらないんだろう
T：大事な問題ですね。ではそれを考えてみましょう。
まず、内分と外分を式で表すと，
\(
\frac{AC}{CB}=\frac{BB'}{B'A}
\)
だから，
\(
\frac{AC}{CB}\cdot\frac{B'A}{B'B}=1
\)
です。
S：ということは、この式を図から導ければ、変わらないことが示せるね。
T：ここで、最初の定理たちを使います。
チェバの定理により
\[
\frac{DF}{FA}\cdot\frac{AC}{CB}\cdot\frac{BG}{GD}=1 \qquad \cdots (1)
\]
メネラウスの定理より
\[
\frac{DF}{FA}\cdot\frac{AB'}{B'B}\cdot\frac{BG}{GD}=1 \qquad \cdots (2)
\]
(1) を変形して，
\[
\frac{DF}{FA}=\frac{CB}{AC}\cdot\frac{GD}{BG}
\]
これを (2) に代入すると，
\[
\frac{CB}{AC}\cdot\frac{GD}{BG}\cdot\frac{AB'}{B'B}\cdot\frac{BG}{GD}=1
\]
よって，
\[
\frac{CB}{AC}\cdot\frac{AB'}{B'B}=1
\]
よって，\(B'\) は外分する点となるので変わらない。
S：えっ？ そうか。さっきのｘを使うのと同じで、この式からｘが１つ決まるね。
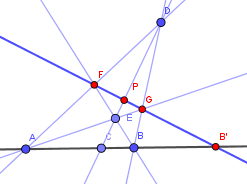T：注意してほしいのは、ＦＢ'についても同じことが言えるから、ＦＢ'とＤＥの交点をＰとすると、ＦＰ：ＰＧ＝ＦＢ'：ＧＢ'が成立ちます。
S：そうか、Ｅを下に動かすと確かに同じことだね。
S：そうすると、ＡＤでもＦ'を取ると同じことが言えそうだよ。
T：さっそく作図をしてみようか。直線ＣＧを引いて、ＡＤとの交点を求める。
S：できた。外分する点（Ｆ'）が求まった。
S：もう一つＢＤについてもＦＣから外分点（Ｇ'）を求めてみよう。
３、三角形の極線
S：あれ、Ｂ'とＦ'とＧ'は一直線上に並んでいる。
T：本当ですか？
S：下の図でＤＥを結ぶとＲを通るよ。Ｂを動かしてもＲを通っている。
S：どうして一直線なんだろう？
S：それは証明できるの？
T：さっきの図を新しく書き直したものを用意したよ。これで確かめてみよう。
T：まず、この形で一直線上にならぶということは、メネラウスの定理の式が成り立つことを言えば良い。
S：どの三角形の使えば良いのかわからなくなるけど、Ｅ,Ｄ,Ｒが直線に並ぶということは、
S：どの三角形を使えば良いのかわからなくなるけど，
E，D，R が一直線に並ぶということは，
\[
\frac{AD}{DB}\cdot\frac{BE}{EC}\cdot\frac{CR}{RA}=1
\]
であることを示せばいい。
S：さっきそれぞれの辺で内分と外分の関係が言えたから，
\[
\frac{AK}{KB}=\frac{AD}{DB},
\qquad
\frac{BI}{IC}=\frac{BE}{EC},
\qquad
\frac{CJ}{JA}=\frac{CR}{RA}
\]
次にチェバの定理から，
一点 \(O\) で交わっているので，
\[
\frac{AK}{KB}\cdot\frac{BI}{IC}\cdot\frac{CJ}{JA}=1
\]
これにさっきの式を代入すると，
\[
\frac{AD}{DB}\cdot\frac{BE}{EC}\cdot\frac{CR}{RA}=1
\]
となるから，メネラウスの定理により，
E，D，R は一直線に並ぶことが言える。
T：すごいね。見事だ。この直線をＯの三角形極線と言います。そして、Ｏを極と言います。
S：これは極から極線を求める証明だけど、この図のように極線から極を求めることができるね。
S：そうか、今度はチェバの定理を言えば良いんだ。同じことだね。
４、内接円錐曲線を作る
S：三角形の極が決まれば極線が決まる。極線が決まれば極が決まる。
S：この極線と円の極線の間にはど関係があるんだろうか？
T：とても素敵な疑問ですね。確かめてみましょう。
S：どうやって確かめれば良いのかな。
S：そうだ。円に外接する三角形を作図すれば確かめることができるかもしれない。
S：やってみよう。この図の線分を直線にして極線を作図すると・・・。
S：ABの距離って焦点の間のことですね。そうか、楕円になるんだ。楕円になっても関係は変わらないということか。
S：この分数の式はチェバの定理からすぐに言えますね。だって接線だから。
T：そうです。この図のＡは内心で頂点と接点を結んだ３線は一点Ｇｅで交わります。
S：直線ＩＥと極線との交点とＤを結ぶと、ＦＧとの交点が円周上にあるのじゃないかな？
T：すごいことに気がつきましたね。もしこれが正しかったら、三角形に内接する楕円が作図できます。
S：証明するにはどうしたらいいんだろう。
T：やってみましょう。まずは説明の図を描いて。
☆円Ａの３接線で作った△FGHについて、ジェルゴンヌ点と内分外分（調和点列）から、
ＮＩとＭＥの交点Ｏは円周上にあることの証明
これを三角形だけで導ければ，
一致法で O は円周上にあることが言える。
まず EPCL について，GDHL が内分外分（調和点列）なので，
\[
\frac{CP}{PE}\cdot\frac{EL}{LC}=1 \qquad \cdots ①
\]
△CLM についてメネラウスの定理により，
\[
\frac{CN}{NO}\cdot\frac{OM}{ME}\cdot\frac{EL}{LC}=1
\qquad \cdots ②
\]
△CEM についてメネラウスの定理により，
\[
\frac{CI}{IO}\cdot\frac{OM}{ME}\cdot\frac{EP}{PC}=1
\qquad \cdots ③
\]
① を変形して，
\[
\frac{PE}{CP}=\frac{EL}{LC}
\]
これを ③ に代入すると，
\[
\frac{CI}{IO}\cdot\frac{OM}{ME}\cdot\frac{EL}{LC}=1
\]
これを ② に代入すると，
\[
\frac{CN}{NO}\cdot\frac{IO}{CI}=1
\]
よって O は円周上にある。
T：素晴らしい。比の関係は射影によっても保たれるので、このことは楕円でも成り立ちます。
S：二番目の図に楕円を作図することができるわけですね。楕円は５点必要だけど、３接点とこの点が３点できるから作図できる。
S：そうすると、三角形の極線を円錐曲線の極線として考えることができるわけですね。
S：二番目の図で作図してみよう。
S：あれ？極線を動かすと双曲線になるよ。そうすると放物線になる時もあるはずだ。
T：極線が重心を通る時に放物線になります。
・・・・
S：極と極線と円錐曲線はワンセットなんだ。
S：この三角形の極線と内接円錐曲線の極線は一致するはずだね。
S：円錐曲線の極線上の点を極とする極線は元の極を通るはずだ。確かめてみよう。
S：あれ？通っていない。どうして？・・・
【２６９、三角形の極と極線と内接二次曲線】
目次へもどる