二次方程式は必ず因数分解できる
二次方程式の解き方
1.二次方程式を解く方法
T:二次方程式を解く方法は何通りもあります。
例えば①完全平方 ②因数分解 ③分解式(α-β)を用いる方法など。
ここで因数分解で解く方法をおさらいしてみましょう。
例えば、x2+6x+8=0…(1) は?
S:足すと6でかけると8になる2数を求めると、4と2だ。
S:どうして足すと6で、かけると8ということがわかるの?
S:この方程式の根をαとβとすると、(x-α)(x-β)=0 だから、展開すると、x2-(α+β)x+αβ=0…(3) となるから。
つまり、(x+4)(x+2)=0とでき、x=-4,-2と解が求まる。
S:解の公式を使わなくても良いから簡単だね。
S:でもこれはいつでも因数分解できるとは限らない。
例えば、x2+6x+1=0…(2) は因数分解できる?
S:足して6、かけて1になる数なんて無いよ。
S:解の公式を使えば、この2つの解を求めることができるから、こういう2数はちゃんとあるよ。
T:そうですね。実は解の公式を使わなくても因数分解できる方法があるんです。
S:そんなことができるんですか?
2.どんな二次方程式も因数分解できる
T:まず(1)を調べてみよう。
足して6になる数はいろいろあるね。
6と0
5と1
4と2
3と3
これを3から見ると、3を中心に対称になっていることに気がつきます。
S:確かに(3+d)と(3-d)になっていますね。
T:そこで、この式を(3)に代入すると、
S:x2+6x+(3+d)(3-d)=0
展開すると和と差の公式により一次の項が消える。これを(2)と比べると、
x2+6x+9-d2=x2+6x+1=0
9-d2=1
d2=9-1=8
d=±√8=±2√2
つまり、
(x+3+2√2)(x+3-2√2)=0
と因数分解できる。
(x=-3±2√2 とわかる)
S:めちゃくちゃ簡単だ。(1)の場合だと、9-d2=8 でd=1となり、さっきの4と2が簡単に求まる。
S:えっ、どうして?
3.足してbになる数
S:3は6÷2で求めるんでしょう。5だったら2.5なのかな?
T:いい質問ですね。これを一般化してみましょう。
まず、二次方程式を x2+bx+c=0 とします。
そうすると、(3)より α+β=-b, αβ=c となります。
ここでα+βを足して-bになる二つの数に分ける工夫をします。
α,β=-b/2±d …(4) とおいて、αβに代入すると
αβ=(-b/2+d)(-b/2-d)=b2/4-d2=c となってdが求まります。
S:y=x2+bx+c としてグラフにしてみよう。ちゃんと-b/2で対称になっている。
S:これで解の公式を求めることもできるよ。
S:計算してみよう。
4.なぜ
T:この方法を発見した人は、数学者のポーシェン・ロー氏。
たまたま[ナゾロジー]というサイトを見ていて見つけました。
S:質問があります。
どうして(4)とおけるんですか?
S:それに(4)とおくどうして解けるんですか? 和と差の公式が大事だということはわかるけど。
S:なぜこういうことに気がついたのですか?
S:三次方程式にも当てはまるのかな?
S:他の解き方と同じところや異なるところは何かな?
S:分解式との違いが気になるな。
T:とてもいい質問ですね。これからやってみましょう。
まず完全平方の求め方は、正方形にすることで平方根がわかりχを求めることができます。
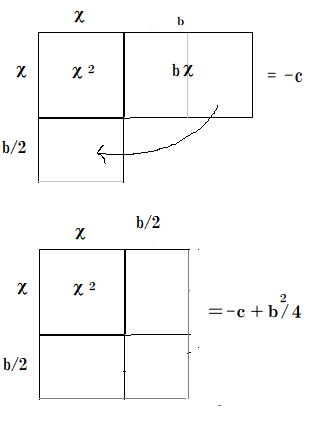
平方根をとって x+b/2=±√(-c+b2/4)
と求めることができます。
⇒詳しくは【数学アラビアンナイト】のページへ
一方因数分解法では、長方形にして面積を0にすることで求めます。
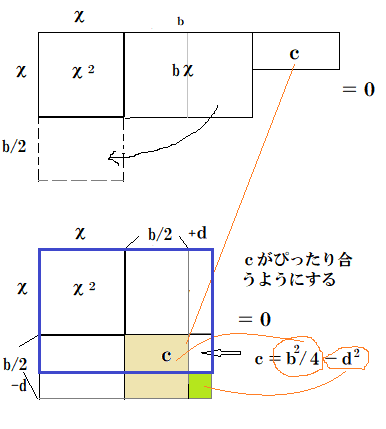
普通はcは合いませんが、bを半分にして同じdを加減するこの方法だと、面積がcとぴったり合うようにできて、長方形になるのです。
c=b2/4-d2
d=±√(b2/4-c)
S:このcの長方形と二つの正方形の差が同じになる所がポイントなんですね。
S:なるほど、長方形と正方形か。こんなところで展開の公式が役立っているんだな。
S:どちらの方法でもb/2が重要な役目を果たしているんですね。
T:以前、因数分解で解の公式を求められないかと考えたことがあるんだけど、
b/2に気が付かなかったから求めることができなかったんだ。
S:でも不思議ですねぇ。
実際に方程式を長方形にしながら理解を深めよう。
目次へもどる

