丂拞妛惗偵傕傢偐傞僈儘傾棟榑
拞妛惗偵傕傢偐傞僈儘傾棟榑偺帋傒
曽掱幃偼側偤夝偗傞偺偐
侽丄曽掱幃偼側偤夝偗傞偺偐
丂僈儘傾棟榑傪傢偐傝堈偔昞尰偡傞偵偼偳偆偟偨傜椙偄偺偩傠偆偐丅
乽傢偐傞乿偲偄偆偙偲傪捛媮偟偰偒偨巹偵偲偭偰丄偄偮偐帋傒偨偄僥乕儅偩偭偨丅
丂偦偺帋傒偼丄傛偔抦偭偰偄傞擇師曽掱幃偐傜巒傔傞偲偄偆傕偺丅
偦偟偰丄徹柧側偟偱懱尡揑僗僩乕儕乕偱僀儊乕僕傪偮偐傫偱偄偔偲偄偆曽朄傪偲傞丅
寁嶼偼戝曄偩偗偳丄拞妛惗偵傕偱偒傞寁嶼偩丅墧昅傪帩偭偰寁嶼偟側偑傜撉傒恑傔偰梸偟偄丅
丂僈儘傾棟榑偺帩偭偰偄傞怺偄巚憐偼丄尰戙偺條乆側壢妛偵媦傫偱偄傞丅
傢偐傜側偄偙偲傪挷傋傞偲偒偵丄偡偱偵椙偔抦偭偰偄傞偙偲偲懳斾偟側偑傜棟夝偟偰偄偔丅
偦偺棟夝偲偄偆峴堊偑傑偝偵僈儘傾偺懳墳側偺偩丅
丂巹偼偦偺懳墳傪乽巜偟帵偟乿偲屇傫偱偄傞偑丄
妛傇偲偄偆峴堊傕偦偺乽巜偟帵偟乿偑巜偟帵偟偰偄傞偙偲傪尒傞偙偲偵懠側傜側偄偲巚偆丅
僈儘傾偺巜偟帵偟偨傕偺偲偼偳傫側偙偲偩偭偨偺偐丄堦弿偵峫偊偰傒傛偆丅
偝偰丄侾師曽掱幃偼桳棟悢偺斖埻偱昁偢夝偗傞丅偙偙偱偼學悢偼桳棟悢(俻)偲偟傛偆丅
侾丄擇師曽掱幃偺夝偒曽乮姰慡暯曽偐傜懳徧幃傊乯
擇師曽掱幃丂倃2亄倎倃亄倐亖侽丂丂丒丒丒(1)
偺崻傪兛丆兝偲偡傞偲丄乮崻偼桳棟悢偱偼側偄乯
丂(倃亅兛)(倃亅兝)亖侽丂偩偐傜丄揥奐偡傞偲
丂倃2亅(兛亄兝)倃亄兛兝亖侽丂丒丒丒乮2乯偲側傞丅
偮傑傝丄
丂兛亄兝亖亅倎
丂兛兝亖倐
偱偁傞丅偙偺幃傪俀師偺婎杮懳徧幃偲尵偆丅
懳徧幃乮兛偲兝傪擖傟懼偊偰傕曄傢傜側偄幃乯偩偭偨傜丄
偙偺婎杮懳徧幃傪慻傒崌傢偣偰嶌傞偙偲偑偱偒傞偺偱丄倎偲倐偺慻崌傢偣偱兛偲兝傪媮傔傞偙偲偑偱偒傞丅
亂偙偺懳徧幃偵偮偄偰偼偙偺僒僀僩偵徻偟偄亀係師曽掱幃偺戙悢揑夝朄偵偮偄偰亁亃
偙偙偱兛偲兝偼擖傟懼偊偰傕(1)傗(2)偺抣偼曄傢傜側偄偲偄偆惈幙傪棙梡偡傞丅
偮傑傝丄擖傟懼偊偰傕曄傢傜側偄幃偼懠偵側偄偐扵偟偰傒傛偆丅
兛亄兝亖亅倎丂偩偐傜丄師偵兛亅兝傪峫偊偰傒傞丅
S丗側偤兛亅兝側偺丠
T丗偙偆偡傟偽楢棫曽掱幃偱夝偗傞偐傜丅偦傟偵兛偲兝傪擖傟懼偊偰傕丄幃偺抣偼亄亅偑堘偆偩偗丅
偙偺幃偼懳徧幃偱偼側偄偺偱倎傗倐偱昞偡偙偲偼偱偒側偄丅
偱傕丄俀忔偡傟偽懳徧幃乮兛偲兝傪擖傟懼偊偰傕摨偠抣傪偲傞乯偵側傞丅
丂乮兛亅兝乯2亖兛2亅2兛兝亄兝2
丂丂丂丂丂丂丂亖兛2亄2兛兝亄兝2亅係兛兝
丂丂丂丂丂丂丂亖(兛亄兝)2亅係(兛兝)
丂丂丂丂丂丂丂亖倎2亅係倐丒丒丒(3)
偙偺傛偆偵婎杮懳徧幃偱昞偡偙偲偑偱偒傞偺偱丄學悢倎丆倐偱抲偒姺偊傞偙偲偑偱偒傞丅
(3)偺暯曽崻傪偲偭偰丄
丂兛亅兝亖亇併(倎2亅係倐)丂丂乮併偺拞偼侽偱偼側偄乯
偡傞偲丄楢棫曽掱幃偑偱偒偰
丂L1亖兛亄兝亖亅倎
丂L2亖兛亅兝亖亇併(倎2亅係倐)
偩偐傜丄俴1偲俴2傪懌偟偰
丂俀兛亖亅倎亇併(倎2亅係倐)
丂丂兛亖{亅倎亇併(倎2亅係倐)}乛俀丂丒丒丒(4)
俴1偐傜俴2傪堷偔偲
丂丂兝亖{亅倎[-+]併(倎2亅係倐)}乛俀丂丒丒丒(5)
偲側偭偰夝偺岞幃偑尒偮偐傞丅
S丗夝偺岞幃偼倃亖{亅b亇併(b2亅4ac)}/2a 偲妎偊偰偄傞偗偳丅
T丗倎倃2亄倐倃亄們亖侽丂傪倎偱妱偭偰丄
丂丂倃2亄(倐乛倎)倃亄(們乛倎)亖侽丂偲偟偰寁嶼偡傟偽丅
S丗偁偭丄偪傖傫偲弌偰偔傞偹丅
偙傟偼學悢偑桳棟悢偺擇師曽掱幃偺崻偺恾偱偡丅懱偺僀儊乕僕傪懱姶偟偰偔偩偝偄丅
俀丄乽懱乿偲偄偆悢偺悽奅乮擇師曽掱幃偼側偤夝偗傞偺偐乯
偝偰丄偙偙偱峫偊偨偄偺偑崻偺岎姺偺堄枴偱偁傞丅
兛偲兝傪岎姺偡傞偲偄偆偙偲偼(4)(5)傪尒傞偲丄亄偲亅偺岎姺偵側偭偰偄傞偙偲偵婥偑偮偔丅
丂倎2亅係倐亖俢丂偲偡傞偲丄兛佁兝偼丂併俢佁亅併俢偲偄偆偙偲偩丅
偱傕丄併俢仺亅併俢傪曄偊偰偟傑偆偲丄懳徧幃偼椙偄偗傟偳丄懠偺幃偱偼曄傢偭偰偟傑偄丄寁嶼偑傔偪傖偔偪傖偵側偭偰偟傑偆丅
偙傟偼偳偆峫偊偨傜椙偄偺偩傠偆偐丅
帇揰傪曄偊偰傒傛偆丅
嵟弶丄學悢偼桳棟悢偲峫偊偨丅偮傑傝丄桳棟悢偺悽奅偺拞偩偗偱偼擇師曽掱幃偼夝偗側偄乮場悢暘夝偱偒側偄乯丅
偱偼丄偳偆偄偆悽奅偩偭偨傜擇師曽掱幃偑夝偗傞偺偐偲偄偆偲丄桳棟悢偵併俢傪晅偗懌偟偨悢偺悽奅偺拞偱偩丅
偦偺悽奅偼偳偆偄偆悢偺悽奅偐丅
幃偱昞偡偲丄
丂倎亄倐併俢丂乮倎丆倐丆俢偼桳棟悢乯
偙偺悢偺悽奅偵偼桳棟悢偑娷傑傟傞丅乮倐亖侽偺帪乯
偦偟偰丄偙偺悢偺悽奅偱偼丄偙偺悢傪寁嶼偟偰傕偦偺寢壥偼昁偢倎亄倐併俢偲側傞丅
懌偟嶼偼偡偖偵傢偐傞偲巚偆丅
偐偗嶼偼丄
丂(倎亄倐併俢)(倎'亄倐'併俢)亖(倎倎'亄倐倐'俢)亄(倎倐'亄倎'倐)併俢
偲側偭偰丄傗偭傁傝倎亄倐併俢偺宍偵側傞丅懠偺併偑弌偰偙側偄偺偩丅妱傝嶼傕摨偠丅暘攝朄懃傕惉傝棫偮丅偙偺悢偺悽奅傪乽懱乿偲偄偆丅
偝偰丄偙偙偱併俢仺亅併俢偺堄枴傪峫偊傞偲丄倎偼曄偊側偄偱丄併俢偺晞崋傪曄偊傞偲偄偆偙偲偵側傞丅
偦傟偼丄倎亄倐併俢偺悢偺悽奅偺寁嶼傪偳偆曄偊傞偺偩傠偆偐丅
偙偺曄姺偼娭悢偲峫偊傞偙偲偑偱偒傞偺偱倖(倎亄倐併俢)亖倎亅倐併俢丂偲偡傞乮併俢偩偗晞崋傪擖傟懼偊傞乯丅
丂倖{(倎亄倐併俢)亄(倎'亄倐'併俢)}
丂丂亖倖{(倎亄倎')亄(倐亄倐')併俢}
丂丂亖(倎亄倎')亅(倐亄倐')併俢
丂丂亖(倎亅倐併俢)亄(倎'亅倐'併俢)
丂丂亖倖(倎亄倐併俢)亄倖(倎'亄倐'併俢)
偲側傝丄懌偟嶼傕偦偺傑傑寁嶼偱偒傞偙偲偵側傞丅偝傜偵丄偐偗嶼傕傗偭偰傒傛偆丅
丂倖{(倎亄倐併俢)丒(倎'亄倐'併俢)}
丂丂亖倖{(倎倎'亄倐倐'俢)亄(倎倐'亄倎'倐)併俢}
丂丂亖(倎倎'亄倐倐'俢)亅(倎倐'亄倎'倐)併俢
丂倖{(倎亄倐併俢)丒倖(倎'亄倐'併俢)}
丂丂亖(倎亅倐併俢)丒(倎'亅倐'併俢)
丂丂亖(倎倎'亄倐倐'俢)亅(倎倐'亄倎'倐)併俢
偱摨偠偵側傞丅倎亄倐併俢傪倎亅倐併俢偵堏偟偰傕丄寁嶼偺峔憿偼惉傝棫偭偰偄傞丅
偙傟傪帺屓摨宆乮幨憸乯偲偄偆丅乮偝傜偵尵偊偽倖丒倗乮兛乯亖倖乮倗乮兛乯乯偲偡傟偽埵悢俀偺孮偵側傞乯
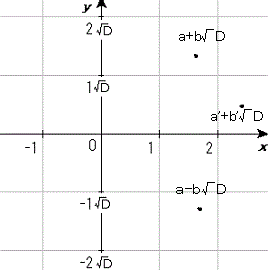 偙偺暯柺乮倎亄倐併俢偺悽奅乯偼丄倃幉偵懳偟偰懳徧偵側偭偰偄傞丅
偙偺暯柺乮倎亄倐併俢偺悽奅乯偼丄倃幉偵懳偟偰懳徧偵側偭偰偄傞丅
偙偺恾偺拞偱懌偟嶼傪昞偟偰傒傛偆乮帋偟偵丄(倎亄倐併俢)亄(倎丩亄倐丩併俢)傪恾偵昞偟偰傒傛偆乯丅
懌偟嶼偼暯峴巐曈宍偵側傞丅偮傑傝儀僋僩儖偲帡偰偄傞丅
偙傟帺懱偑晄巚媍側偺偩偑丄偙偆偄偆懳徧惈偑偁傞悽奅偲偄偆偙偲側偺偩丅
偙偺倎亄倐併俢偺悽奅傪俻(併俢)偲昞偡丅
偦偟偰丄偙偺悽奅偱偼擇師曽掱幃偼場悢暘夝偱偒偰夝傪媮傔傞偙偲偑偱偒傞丅
S丗偠傖偁丄惍悢偱儅僀僫僗偲僾儔僗傪擖傟懼偊偰傕摨偠偙偲偑尵偊傞偺丠
S丗偦偆側傟偽丄挋嬥偺懡偄恖偲庁嬥偺懡偄恖偑媡揮偡傞傛丅
T丗惍悢偺悽奅偱偼亄偲亅偼懳徧偵尒偊傞偗偳丄懳徧偱偼柍偄強偑偁傞傫偩丅
丂(亅)亊(亅)亖(亄)偩傠丅偙傟偑丄擖傟懼偊傞偲(亄)亊(亄)亖(亅)偲側偭偰搒崌偑埆偔側傞丅
丂懌偟嶼偩偗偩偭偨傜侽偱懳徧側傫偩偗偳丄偐偗嶼偼侾傪拞怱偲偟偰偱懳徧偩偐傜僟儊側傫偩側丅
S丗偮傑傝丄倷幉偱偼懳徧偵側傜側偄傫偩側丅
亂曽掱幃偲懱偺奼戝偵偮偄偰丄宑墳戝妛偺嶁撪嫵庼偺價僨僆偑偁傞丅
丂摿偵曽掱幃偵傛傞戙悢揑奼戝傪丄
懡崁幃娐偺僀僨傾儖偱妱偭偰偄傞強偑偲偰傕椙偄亃
俁丄嶰師曽掱幃偺夝偒曽
偙偙偱丄嶰師曽掱幃丂倃3亄倎倃2亄倐倃亄們亖侽丒丒丒(6)
偵偮偄偰摨偠傛偆偵峫偊偰傒傛偆丅傕偪傠傫崻偼桳棟悢偱偼側偄乮亖俻偱婛栺乯
丂(倃亅兛)(倃亅兝)(倃亅兞)
丂丂亖倃3亅(兛亄兝亄兞)倃2亄(兛兝亄兝兞亄兞兛)倃亅兛兝兞
丂丂亖侽丂丒丒丒(7)
(6)偲斾妑偟偰俁師偺婎杮懳徧幃傪嶌傞丅
丂兛亄兝亄兞亖亅倎
丂兛兝亄兝兞亄兞兛亖倐
丂兛兝兞亖亅們
偙傟偲乽崻偺岎姺乿傪巊偭偰嶰師曽掱幃偺夝偺岞幃傪媮傔偰傒傛偆丅
偙偙偱丄崻偺岎姺傪峫偊偰傒傞偲丄俁両亖俇屄偁傞丅
俀師偺応崌偼俀捠傝乮乽曄偊側偄乿傕擖傟偰乯偟偐側偐偭偨偑丄堦婥偵憹偊偨丅
丂乮兛兝兞乯乮兛兞兝乯乮兝兛兞乯乮兝兞兛乯乮兞兛兝乯乮兞兝兛乯
傑偢丄崻傪偳偺傛偆偵擖傟懼偊偰傕(6)偺幃偺抣偼曄傢傜側偄乮懳徧偱偁傞乯丅
偙偙偱丄捈愙崻傪媮傔傞偺偼擄偟偄偺偱丄擇師曽掱幃偲摨偠傛偆偵兛丆兝丆兞傪巊偭偨拞娫偺幃傪峫偊傞丅偨偩丄偙偺応崌侾偺俁忔崻傪巊偆丅
S丗側偤丠
T丗俀師偺帪偼侾偺俀忔崻傪巊偭偨傛丅
S丗侾偺俀忔崻偭偰亅侾偱偟傚丅偳偙偱巊偭偨偺丠
T丗兛亅兝亖兛亄(亅1)兝偱巊偭偨傛丅
S丗侾偺俁忔崻偭偰丠
T丗倃3亖侾偲側傞倃丅
S丗偦傫側偺侾偱偟傚丅
T丗幚偼戙悢曽掱幃偱戝帠側偙偲偑偁傞丅偦傟偼丄嶰師曽掱幃偩偭偨傜昁偢崻偑俁偮偁傞乮廳崻傪娷傫偱乯偲尵偆偙偲側傫偩丅偩偐傜侾偺懠偵偁偲擇偮偁傞丅
丂丂倃3亅侾亖(倃亅侾)(倃2亄倃亄侾)亖侽
丂偙傟偼丄倃亅侾亖侽枖偼倃俀亄倃亄侾亖侽偩偐傜丄
丂丂倃2亄倃亄侾亖侽傪夝偗偽偄偄丅
丂丂倃亖{亅侾亇併(亅3)}乛俀
S丗併偺拞偵儅僀僫僗偑弌偰偔傞偗偳丄偳偆偄偆堄枴丠
T丗俀忔偡傞偲亅俁偵側傞悢傪峫偊傞偲偄偆偙偲側傫偩丅
丂偦偆偡傞偲丄傛傝峀偄悢偺悽奅偑峀偑偭偰偔傞丅
丂{亅侾亄併(亅3)}乛俀亖冎偲偡傞偲
丂丂冎2亖{(亅侾亄併(亅3)}乛俀)2亖({亅侾亅併(亅3)}乛俀
丂偲側偭偰偟傑偆丅傕偪傠傫冎3亖侾丂丆丂冎2亄冎亄侾亖侽
丂偙偙偱丄冎偲兛丆兝丆兞傪巊偭偰俁尦楢棫曽掱幃傪偮偔偭偰傒傛偆丅
丂俴1亖兛亄兝亄兞亖亅倎
丂俴2亖兛亄兝冎亄兞冎2
丂俴3亖兛亄兝冎2亄兞冎
S丗側偤偙偆偄偆幃偵偡傞偺丠
T丗偙偆偄偆場悢暘夝偺幃偑偁傞丅
x3亄y3亄z3亅3xyz亖(x亄y亄z)(x亄冎y亄冎2z)(x亄冎2y亄冎z)
揥奐偡傞偲冎偑徚偊偰偟傑偆傫偩丅
偁偲俴2偲俴3偑傢偐傟偽楢棫曽掱幃偩偐傜丄兛丆兝丆兞偺抣偑傢偐傞丅
偱傕丄俴1偼懳徧幃偩偗偳丄俴2偲俴3偼懳徧幃偱偼側偄丅
偱偼丄偙偺俀偮偺幃偐傜偳偆傗偭偰懳徧幃傪嶌傞偐丅幚偼冎偺惈幙傪巊偆偲娙扨偵偱偒傞丅傑偢偐偗偰傒傛偆丅
丂俴2丒俴3亖(兛亄兝冎亄兞冎2)(兛亄兝冎2亄兞冎)
丂丂丂丂丂亖兛2亄兛兝冎2亄兛兞冎亄兛兝冎亄兝2亄兝兞冎2
丂丂丂丂丂丂丂亄兛兞冎2亄兝兞冎亄兞2
丂丂丂丂丂亖兛2亄兝2亄兞2亄(兛兝亄兝兞亄兛兞)冎
丂丂丂丂丂丂丂亄(兛兝亄兝兞亄兛兞)冎2
丂丂丂丂丂亖兛2亄兝2亄兞2亄(兛兝亄兝兞亄兛兞)(冎亄冎2)
丂丂丂丂丂亖兛2亄兝2亄兞2亄(倐)(亅1)
丂(兛亄兝亄兞)2亖兛2亄兝2亄兞2亄2(兛兝亄兝兞亄兛兞)
偩偐傜
丂俴2丒俴3亖(兛亄兝亄兞)2亅2(兛兝亄兝兞亄兛兞)亅倐
丂丂丂丂丂亖(亅倎)2亅俁倐
偁偲俴2亄俴3偑媮傑傟偽丄擇師曽掱幃傪嶌傞偙偲偑偱偒傞丅
偱傕丄俴2亄俴3亖兛亄兝冎亄兞冎2亄兛亄兝冎2亄兞冎偼懳徧幃偱偼側偄丅
偳偆偟偨傜懳徧幃乮崻傪岎姺偟偰傕曄傢傜側偄幃乯偑偱偒傞偐丅
偙偺幃偺崻傪岎姺偟偰傒傛偆丅岎姺偺応崌偼丄俁両亖俁丒俀丒侾亖俇捠傝偁傞丅
丂俴2亖兛亄兝冎亄兞冎2
丂俴3亖兛亄兝冎2亄兞冎
偙偺応崌俴2偩偗傗偭偰傒傟偽慡偰偺岎姺偑弌偰偔傞乮摨偠偙偲偩偐傜乯丅
丂乮兛兝兞乯丗兛亄兝冎亄兞冎2亖俴2
丂乮兛兞兝乯丗兛亄兞冎亄兝冎2亖兛亄兝冎2亄兞冎亖俴3
丂乮兝兛兞乯丗兝亄兛冎亄兞冎2亖兛冎亄兝亄兞冎2
丂乮兝兞兛乯丗兝亄兞冎亄兛冎2亖兛冎2亄兝亄兞冎
丂乮兞兛兝乯丗兞亄兛冎亄兝冎2亖兛冎亄兝冎2亄兞
丂乮兞兝兛乯丗兞亄兝冎亄兛冎2亖兛冎2亄兝冎亄兞
偙傟偼冎偵拲栚偡傞偲擇偮偵暘椶偱偒傞丅
丂乮兛兝兞乯丗兛亄兝冎亄兞冎2亖兛亄兝冎亄兞冎2亖俴2
丂乮兝兞兛乯丗兝亄兞冎亄兛冎2亖兛冎2亄兝亄兞冎
丂乮兞兛兝乯丗兞亄兛冎亄兝冎2亖兛冎亄兝冎2亄兞丂乮偙傟傜偑嬼抲姺乯
丂乮兛兞兝乯丗兛亄兞冎亄兝冎2亖兛亄兝冎2亄兞冎亖俴3
丂乮兝兛兞乯丗兝亄兛冎亄兞冎2亖兛冎亄兝亄兞冎2
丂乮兞兝兛乯丗兞亄兝冎亄兛冎2亖兛冎2亄兝冎亄兞
偦傟偧傟冎傪偐偗偰偄偔偲弌偰偔傞僌儖乕僾偩丅
乮兛兝兞乯傪曄偊側偄抲姺傪倕偲偡傞偲丄偙偺崻偺抲姺偼冎傪偐偗偰偄偔偲偱偒傞丅
丂丂倕丂丂丂丂丗兛亄兝冎亄兞冎2亖兛亄兝冎亄兞冎2亖俴2
丂丂倕丒冎2丂 丗兝亄兞冎亄兛冎2亖兛冎2亄兝亄兞冎
丂丂倕丒冎丂丂丗兞亄兛冎亄兝冎2亖兛冎亄兝冎2亄兞
丂乮兛兞兝乯丂丂丂 丗兛亄兞冎亄兝冎2亖兛亄兝冎2亄兞冎亖俴3
丂乮兛兞兝乯丒冎丂 丗兝亄兛冎亄兞冎2亖兛冎亄兝亄兞冎2
丂乮兛兞兝乯丒冎2丂丗兞亄兝冎亄兛冎2亖兛冎2亄兝冎亄兞
偦偆偡傞偲丄偙偺偦傟偧傟偺俁偮偺幃傪偐偗傞偲丄
丂e丒(e丒冎2)丒(e丒冎)亖e3亖俴23
丂(兛兞兝)丒(兛兞兝)丒冎丒(兛兞兝)丒冎2=(兛兞兝)3=俴33
偲擇偮偵傑偲傔傞偙偲偑偱偒傞丅寁嶼傪偡傞偲丄
丂俴23亖(兛+兝冎+兞冎2)3
丂丂丂 亖兛3+兝3+兞3亄俇兛兝兞
丂丂丂丂丂亄俁冎(兛2兝+兝2兞+兛兞2)
丂丂丂丂丂亄俁冎2 (兛兝2+兝兞2+兛2兞)
丂俴33亖(兛+兝冎2+兞冎)3
丂丂丂 亖兛3+兝3+兞3亄俇兛兝兞
丂丂丂丂丂亄俁冎2 (兛2兝+兝2兞+兛兞2)
丂丂丂丂丂亄俁冎(兛兝2+兝兞2+兛2兞)
偙偺擇偮偺榓偑懳徧幃偵側傞偙偲偵婥偑偮偔丅
乮偡傋偰偺屳姺偱抣偑曄傢傜側偄傛偆偵嶌偭偨傢偗偩偐傜懳徧幃偵側傞偺偼摉慠乯
丂俴23亄俴33亖俀(兛3亄兝3亄兞3)亄侾俀兛兝兞
丂丂丂丂丂丂丂丂丂丂亄俁(冎亄冎2)(兛兝2亄兝兞2亄兛2兞)
丂丂丂丂丂丂丂丂丂丂亄俁(冎亄冎2)(兛2兝亄兝2兞亄兛兞2)
丂丂丂丂丂丂丂亖俀(兛3亄兝3亄兞3)亄12兛兝兞
丂丂丂丂丂丂丂丂丂丂亄俁(亅1)(兛兝2亄兝兞2亄兛2兞)
丂丂丂丂丂丂丂丂丂丂亄俁(亅1)(兛2兝亄兝2兞亄兛兞2)
丂丂丂丂丂丂丂亖俀(兛3亄兝3亄兞3)亄侾俀兛兝兞
丂丂丂丂丂丂丂丂丂丂亅俁(兛兝2亄兝兞2亄兛2兞
丂丂丂丂丂丂丂丂丂丂亄兛2兝亄兝2兞亄兛兞2)
丂(兛亄兝亄兞)3亖兛3亄兝3亄兞3亄俁(兛亄兝亄兞)(兛兝亄兝兞亄兞兛)亅俁兛兝兞
偩偐傜丄偡傋偰婎杮懳徧幃偵側傝丄偟偨偑偭偰學悢偱昞偡偙偲偑偱偒傞丅
乮俴23亖俼1丂俴33亖俼2丂偲偡傞乯
丂俼1亄俼2亖俀(兛亄兝亄兞)3亅俋(兛亄兝亄兞)(兛兝亄兝兞亄兞兛)亄俀俈兛兝兞
丂丂丂丂丂丂亖俀倎3亄俋倎倐亅俀俈們
傑偨丄偝偭偒偺俴2丒俴3亖倎2亅俁倐傪俁忔偡傞偲丄
丂俼1丒俼2亖(倎2亅俁倐)3
崻偲學悢偺娭學偵傛傝丄俼1偲俼2偼偙傟傪崻偲偡傞擇師曽掱幃
丂俿俀亅乮俼1亄俼2乯俿亄俼1丒俼2亖侽丂傪夝偗偽媮傔傞偙偲偑偱偒傞丅
擇師曽掱幃傪夝偔偲丄
丂俿亖[亅(俀倎3亄俋倎倐亅俀俈們)亇併{(俀倎3亄俋倎倐亅俀俈們)2亅係(倎2亅俁倐)3}]乛俀
偲側偭偰丄俼1偲俼2偑媮傑傞丅
偝傜偵丄偙傟偺俁忔崻傪偲傟偽俴2偲俴3偑媮傑傞丅
偦偟偰丄俁尦楢棫曽掱幃傪夝偗偽兛丆兝丆兞偑媮傑傞丅
丂丂丂兛亄兝亄兞丂丂亖亅倎
丂丂丂兛亄兝冎亄兞冎2亖俴2
丂亄乯兛亄兝冎2亄兞冎亖俴3
丂丂俁兛丂丂丂丂丂亖亅倎亄俴2亄俴3
偲偄偆傛偆偵丅
係丄嶰師曽掱幃偼側偤夝偗傞偺偐
偙偙偱丄偙偺夝偒曽偺堄枴傪扵偭偰傒傛偆丅
傑偢丄戝偒側僗僩乕儕乕偼丄曽掱幃傪夝偔偨傔偵丄抲姺傪棙梡偟偰懳徧幃傪嶌傝丄偦偺懳徧幃偱傛傝彫偝側師悢偺曽掱幃傪嶌偭偰丄夝傪媮傔偰偄偔偲偄偆曽岦偩丅
偙偺懳徧幃偑偄偔偮偱偒傞偺偐偑戝帠側栤戣偱丄偦偺師悢埲忋偺悢偵側偭偰偼堄枴偑側偄丅
偙偺応崌丄俇捠傝偺抲姺偱庢傞抣偑俀捠傝偟偐側偄偲偄偆揰偑夝偗傞億僀儞僩偱偁傞丅
傑偨丄嵟弶偼慡偰偺抲姺偵懳偟偰懳徧偱偁傝丄夝傪媮傔傞偨傔偵曽掱幃傪夝偔乮儀僉崻傪偲傞乯偲丄懳徧惈偑彮偟偢偮曵傟偰偄偔偲偄偆嬝摴偵側偭偰偄傞丅
偮傑傝丄懳徧惈偑彮偟偢偮曵傟偰偄偔偲偄偆偙偲偵懳墳偟偰丄媡偵懱偺悽奅偼奼挘偟偰偄傞丅偦偙傪尒偰傒傛偆丅
偙偺曽掱幃偺崻偼丄桳棟悢偺拞偵偼側偄丅乮敾暿幃偵傛傞偑乯
偱偼丄崻傪偳偺傛偆偵曄宍偡傟偽桳棟悢偺拞偱寁嶼偱偒傞偐丅
傑偢丄崻偵冎傗冎2 傪偐偗傞丅偮傑傝丄a亄b冎傪擖傟傞丅
偦傟偼丄桳棟悢偵冎傪晅偗壛偊傞偙偲偵摉偨傞丅幃偱偄偆偲丄a亄b冎偺悽奅偱偁傞丅
偙偺悽奅偺梫慺偼丄a亄b冎亄c冎2 偲昞偡偙偲偑偱偒傞丅
偙偺悽奅偺拞偱偼丄俁崻偺榓傪俁忔偟偰壛偊傞偲懳徧幃偑偱偒丄學悢偱昞偡偙偲偑偱偒傞丅
偙偺応崌丄懳徧幃偩偐傜崻偺抲姺偼慡偰偺抲姺偵懳偟偰抣傪曄偊側偄丅偙傟傜偼丄慡偰倣亄値冎偺悽奅偺拞偱偱偒傞丅
師偵丄偙偺懳徧幃偐傜擇師曽掱幃偑偱偒傞偺偱夝偔偙偲偑偱偒傞丅
丂俿俀亅乮俼1亄俼2乯俿亄俼1丒俼2亖侽
偙偙偱擇師曽掱幃偱傗偭偨傛偆偵峫偊傞偲丄
丂(俼1亅俼2)2亖(俼1亄俼2)2亅係俼1丒俼2乧嘆丂偲側偭偰懳徧幃偵側傞丅
丂(俼1亅俼2) 亖亇併{(俼1亄俼2)2亅係俼1丒俼2}乧嘇
嘆偺嵍曈偼懳徧幃側偺偵丄嘇偺嵍曈偼懳徧幃偱偼側偄丅
偮傑傝丄嘆偼兛,兝,兞傪偳偺傛偆偵擖傟曄偊偰傕摨偠抣傪偲傞偗偳丄嘇偱偼(俼1亅俼2)偲(俼2亅俼1)偑堘偆偺偱俀偮偺抣偵側偭偰偟傑偆丅
偲偄偆偙偲偼丄併傪偲傞偲懳徧惈偑尭偭偰偄傞偲偄偆偙偲偩丅仺亂徻偟偄夝愢亃
偱偼丄偳傟偔傜偄懳徧惈偑尭偭偰偄傞偺偐偲偄偆偲丄
崻偺嬼抲姺乮(123)亖(12)(23)偲偄偆傛偆偵嬼悢偺屳姺偱偱偒偰偄傞抲姺乯偱偼亇(俼1亅俼2)偺抣偼曄傢傜側偄丅
偮傑傝丄嬼抲姺偱偼惉傝棫偭偰偄傞丅
偙傟傑偱崻偺抲姺傪峫偊偰偒偨偑丄曽掱幃傪夝偔偲偒偵丄
崻偺抲姺偑廳梫側堄枴傪帩偭偰偄傞偙偲偑偍傏傠偘側偑傜晜偐傫偱偔傞丅
偦偙偱丄偙偺抲姺偦偺傕偺偺廤傑傝傪峫偊傞偲丄堦偮偺峔憿傪帩偭偰偄傞偙偲偵婥偑偮偔丅
偦傟偵偮偄偰偼屻偱庢傝忋偘傞偑丄偲傝偁偊偢俁偮偺崻偺抲姺傪俁師偺懳徧孮俽3偲偄偆丅
嬼抲姺偺廤傑傝傕孮偲側傞丅
偦偟偰丄嬼抲姺偼俽3偺晹暘廤崌偱偁傞偲摨帪偵晹暘孮偵側傝丄偙傟傪岎戙孮俙3偲尵偆丅
S丗併傪偲偭偰傕丄俇偮偺抲姺偺偆偪敿暘偺嬼抲姺偱偼惉傝棫偭偰偄傞偺偱偡偹丅
T丗偦偟偰丄3併丂傪庢傞偲懳徧惈偼姰慡偵夡傟丄孮乮惉傝棫偮抲姺乯偼倕乮曄偊側偄抲姺乯偺傒偵側傞丅
丂倕偺傒偺孮乮抲姺乯偵側偭偨偲偒丄偦偺曽掱幃偼夝偗偨偲偄偆丅
丂懱偺曽偱偄偆偲丄偦傟偼尦偺懱傪偩傫偩傫奼挘偟偰偄偔偙偲偵偁偨傞丅孮乮抲姺乯偺曽偼偩傫偩傫彫偝偔側偭偰偄偔丅
S丗僈儘傾偼偙偺孮偲懱偺娭學傪尒敳偄偨傫偩丅
S丗偙偺懱偺曽偺娭學傕柺敀偄傛丅曽掱幃偺岞幃偼檖崻傪巊偆傫偩丅
丂丂丂丂丂丂丂丂懱丂丂丂丂丂丂孮乮抲姺乯
丂丂俻(冎)亖俴丂丂仜丂丂丂丂仜丂嶰師曽掱幃偺懳徧孮乮崻偺抲姺乯亖俽3
丂丂丂丂丂丂丂丂丂乥丂丂丂丂乥
丂丂丂丂丂丂丂丂丂乥丂丂丂丂乥丂擇師曽掱幃偵偡傞
丂丂俴(併俢)亖俵丂仜丂丂丂丂仜丂併傪偲傞亖嬼抲姺偱曄傢傜側偄
丂丂丂丂丂丂丂丂丂乥丂丂丂丂乥丂俙3亖岎戙孮
丂丂丂丂丂丂丂丂丂乥丂丂丂丂乥
丂丂俵(3併俼)亖俶 仜丂丂丂丂仜丂3併傪偲傞
丂
丂丂丂丂丂丂丂丂丂丂夝偗偨両
S丗偙傟傪擇師曽掱幃偵摉偰偼傔傞偲偳偆側傞偺丠
T丗椙偄栤戣偩偹丅傗偭偰傒傛偆丅
丂丂丂丂丂丂丂丂懱丂丂丂丂丂丂孮乮抲姺乯
丂丂俻(桳棟悢)丂丂仜丂丂丂丂仜丂俀師曽掱幃偺懳徧孮乮崻偺抲姺乯亖俽2亖{e丆(1,2)}
丂丂丂丂丂丂丂丂丂乥丂丂丂丂乥丂丂擇偮偺崻傪擖傟懼偊偰傕(懳徧)幃偺抣偼曄傢傜側偄
丂丂丂丂丂丂丂丂丂乥丂丂丂丂乥
丂丂俻(併俢)丂丂丂仜丂丂丂丂仜丂併傪偲傞亖{倕}丂佀崻偺懳徧惈偼柍偔側傞亖崻偑尒偮偐傞
丂丂丂丂伀丂丂丂丂丂丂夝偗偨両
丂丂倎+倐併俢偺悽奅偱偼場悢暘夝偱偒傞
S丗偮傑傝曽掱幃偑夝偗傞悽奅(懱)偲崻偺抲姺偲偺娭學偵偼枾愙側娭學偑偁傞偲偄偆偙偲偱偡偹丅
俆丄抲姺孮傪挷傋傞乧崻偺抲姺偼孮偱偁傞
桳棟悢偵冎偲冎2 傪壛偊偨悽奅俻(冎)偱偼俁偮偺崻偺懳徧幃傪嶌傞偙偲偑偱偒傞丅
偮傑傝丄俁偮偺崻偺抲姺偼偡傋偰惉傝棫偭偰偄傞丅
偙偺抲姺偼俁両亖俁亊俀亖俇捠傝偁偭偰丄抲偒姺偊傪墘嶼偲偟偰孮傪側偡丅
傢偐傝堈偔偡傞偨傔偵昞傪嶌偭偰傒傛偆丅
(23)偼崻偵斣崋傪偮偗丄俀斣栚偲俁斣栚傪擖傟懼偊傞丅(123)偼1仺2仺3仺1偲抲偒懼偊傞抲姺傪昞偡丅
(123)(123)偼丄兛兝兞傪(123)偲抲偒姺偊傞偲兞兛兝偲側傝丄偝傜偵(123)偲抲偒姺偊傞偲兝兞兛偲側傞丅
偙傟偼兛兝兞傪(132)偲抲偒姺偊偨傕偺偲摍偟偄偺偱丄(123)(123)亖(132)偲傒側偡偙偲偑偱偒傞丅
丂
丂丂丂丂丂|丂倕丂丂乮123乯丂乮132乯丂乮12乯丂乮13乯丂乮23乯
丂丂丂倕丂|丂倕丂丂乮123乯丂乮132乯丂乮12乯丂乮13乯丂乮23乯
丂丂 (123)|乮123乯 乮132乯丂丂 倕丂丂乮23乯丂乮12乯丂乮13乯
丂丂 (132)|乮132乯丂 倕丂丂 乮123乯丂乮13乯丂乮23乯丂乮12乯
丂丂丂(12)|乮12乯丂乮13乯丂丂乮23乯丂丂倕丂 乮123乯 乮132乯
丂丂丂(13)|乮13乯丂乮23乯丂丂乮12乯丂乮132乯丂 倕丂 乮123乯
丂丂丂(23)|乮23乯丂乮12乯丂丂乮13乯丂乮123乯乮132乯丂 倕
偙偺孮傪俁師偺懳徧孮俽3偲偄偆丅偙偺昞傪巊偆偲丄偝偭偒偺暘椶偼師偺傛偆偵側傞丅
丂e丂亖乮兛兝兞乯亖兛亄兝冎亄兞冎2
丂e(123)(123)亖e(132)亖e亊冎2亖乮兝兞兛乯亖兛冎2亄兝亄兞冎
丂e(123)亖e亊冎亖乮兞兛兝乯亖兛冎亄兝冎2亄兞
丂(23)亖乮兛兞兝乯亖兛亄兝冎2亄兞冎亖俴俁
丂(23)(123)亖(12)亖乮兛兞兝乯亊冎亖乮兝兛兞乯亖兛冎亄兝亄兞冎2
丂(23)(123)(123)亖(13)亖乮兞兝兛乯亊冎2亖兛冎2亄兝冎亄兞
偙偺暘椶偼丄乷e丆(123)丆(132)乸偲乷(23)丆(12)丆(13)乸偵暘偗傜傟傞偐傜偱偒偨偙偲偵側傞丅
慜偺曽偺抲姺偼(123)亖冃亖冎偲偡傞偲丄冃2亖(132)亖冎2 偩偐傜丄
乷e丆(123)丆(132)}亖乷e丆冃丆冃2乸亖俙3丂偲側傝丄弰夞孮(冃偩偗偱惗惉偝傟傞孮)偲側傞丅
偦偟偰丄昞偐傜側偤冎偲冎2偵側偭偰偄傞偺偐傕傢偐傞丅
傑偨丄俙3偼嬼抲姺乮椺偊偽丄(123)1亖(12)(23)偺傛偆偵嬼悢屄偺屳姺偐傜偱偒偰偄傞抲姺乯
偺廤傑傝偱丄嬼抲姺偳偆偟偺墘嶼偼傕偪傠傫嬼抲姺偵側傞偐傜孮傪側偟丄
俽3偺晹暘孮偵側偭偰偄傞丅
偝傜偵丄偙偺孮偼尦偺孮傪擇偮偵暘偗傞丅
偙偺晹暘孮俙傪堦偮偵傑偲傔倕乮扨埵尦乯偲偡傞偲丄乷倕俙丆(23)俙乸偲偄偆怴偨側孮乮俽3乛俙3乯偑偱偒傞丅
偙傟傪忚梋孮偲偄偆丅偙傟偵偮偄偰偼屻偱偲傝偁偘傞丅
嶰師曽掱幃偑夝偗偨偺偼丄崻偺抲姺偼俇庬椶偁傞偗偳丄偦偺抣偼俀庬椶偵側偭偰偟傑偆偐傜偩丅
丂丂丂丂丂丂丂丂懱丂丂丂丂丂丂孮
丂丂俻(冎)亖俴丂丂仜丂丂丂丂仜嶰師曽掱幃偺懳徧孮俽3亖{倕,冃,冃2,冄,冃冄,冃2冄}
丂丂丂伀丂丂丂丂丂乥丂丂丂丂乥丂丂伀晹暘孮
丂丂丂奼戝丂丂丂丂乥丂丂丂丂乥丂俀師曽掱幃偵偡傞
丂丂俴(併俢)亖俵丂仜丂丂丂丂仜併傪偲傞亖嬼抲姺偱曄傢傜側偄
丂丂丂伀丂丂丂丂丂乥丂丂丂丂乥丂岎戙孮俙3亖乷倕,冃,冃2乸
丂丂丂奼戝丂丂丂丂乥丂丂丂丂乥丂丂伀晹暘孮
丂丂俵(3併俼)亖俶 仜丂丂丂丂仜丂3併傪偲傞乷倕乸
丂
丂丂丂丂丂丂丂丂丂丂夝偗偨両
S丗孮偲曽掱幃傪夝偔偙偲偺娭學偑壗偲側偔僀儊乕僕偱偒偨傛偆側婥偑偡傞丅
S丗晹暘孮偲奼戝懱偑懳墳偟偰偄傞偹丅
俇丄巐師曽掱幃偺夝偒曽
師偼巐師曽掱幃傪摨偠傛偆偵夝偄偰傒傛偆丅
丂倃4亄倫倃3亄倯倃2亄倰倃亄倱亖侽丒丒丒(1)
偺崻傪倎丆倐丆們丆倓偲偡傞丅崻偲學悢偲偺娭學乮婎杮懳徧幃乯偼丠
S丗(x-a)(x-b)(x-c)(x-d)=0傪揥奐偡傟偽椙偄丅
崻偲學悢偺娭學偼丄
丂倎亄倐亄們亄倓亖亅倫
丂倎倐亄倎們亄倎倓亄倐們亄們倓亖倯
丂倎倐們亄倎倐倓亄倎們倓亄倐們倓亖亅倰
丂倎倐們倓亖倱
T丗係尦楢棫曽掱幃偵尒偊傞偑丄偙傟傪夝偔偲(1)偵栠偭偰偟傑偆丅偙偙偵傕偆堦偮丄崻偺娭學幃傪嶌傝偩偟偰傒傛偆丅
偦傟偼丄(倎亄倐)亅(們亄倓)偲偄偆幃丅乮偙偺暘夝幃偼偄傠偄傠峫偊傜傟傞丅杮摉偼倝傪巊偭偰傗傝偨偐偭偨偗偳寁嶼偑戝曄両乯
偲偙傠偑丄偙偺抣偑傢偐傜側偄丅傢偐傜側偄偑丄懳徧幃偵偡傟偽婎杮懳徧幃偐傜學悢偱昞偡偙偲偑偱偒傞丅
傑偢丄嶰師曽掱幃偱傗偭偨傛偆偵丄偙偺幃偵抲姺傪巤偟偰傒傞丅抲姺偼慡晹偱係両亖4丒3丒2丒1亖俀係捠傝丅
偙偺俀係捠傝傪慡偰巤偟偰傒傞偲丄俇捠傝偺抣傪偲傞偙偲偑傢偐傞丅
幚嵺偵崻偵斣崋傪怳偭偰丄侾俀俁係偲暲傋傞偲偳偆曄傢偭偰偄傞偐挷傋傞丅
丂侾俀俁係丂佀丂倕
丂侾俀係俁丂佀丂(俁係)
丂俀侾俁係丂佀丂(侾俀)
丂俀侾係俁丂佀丂(侾俀)(俁係)
偙傟偼摨偠抣偵側傞丅
丂俁係侾俀丂佀丂(侾俁)(俀係)
丂俁係俀侾丂佀丂(侾係俀俁)
丂係俁侾俀丂佀丂(侾俁俀係)
丂係俁俀侾丂佀丂(侾係)(俀俁)
偙傟偼晞崋偑亅偵側傞丅偲偄偆偙偲偼俀忔偡傟偽摨偠抣偵側傞丅
俉捠傝偑摨偠抣偵側傞偺偩偐傜丄俀係亐俉亖俁偲側傝丄懠偵傕偁偲俀捠傝偺幃偑媮傑傞丅
偦傟偼丄(倎亄們)亅(倐亄倓)偲(倎亄倓)亅(倐亄們)
俀忔偟偰
丂俴1亖((倎亄倐)亅(們亄倓))2
丂俴2亖((倎亄們)亅(倐亄倓))2
丂俴3亖((倎亄倓)亅(倐亄們))2
偙偺俁偮偺幃傪帋偟偰傒傟偽丄偦傟偧傟俉捠傝偺抲姺偱摨偠抣偵側傝丄偡傋偰偺抲姺偱偼堎側傞抣傪庢傞偙偲偑傢偐傞丅
偙傟傪懳徧幃偵偡傞偨傔偵偼丄慡偰偺屳姺乮慡偰偺抲姺偱側偔偰傕乯偱丄幃偺抣偑曄傢傜側偄傛偆偵偟側偗傟偽側傜側偄丅
偦偺偨傔偵偼俴1,俴2,俴3偺婎杮懳徧幃傪嶌傞丅
傑偢丄俴1亄俴2亄俴3傪寁嶼偟偰傒傛偆丅
偙偺寁嶼偼丄http://www.wolframalpha.com/丂偵擟偣傟偽椙偄丅
壓偺悢幃傪擖椡偟偰傒傛偆丅
丂(a+b-c-d)2+(a+c-b-d)2+(a+d-b-c))2
丂=3a2-2ab-2ac-2ad+3b2-2bc-2bd+3c2-2cd+3d2
丂=3(a2+b2+c2+d2)-2(ab+ac+ad+bc+bd+cd)
S丗(倎亄倐亄們亄倓)2
亖倎2亄倐2亄們2亄倓2亄俀(倎倐亄倎們亄倎倓亄倐們亄倐倓亄們倓)
偩偐傜丄倎2亄倐2亄們2亄倓2亖倫2亅俀倯偩偹丅
偡傞偲丄俴1亄俴2亄俴3亖俁倫2亅俉倯偩丅
丂俴1亄俴2亄俴3亖俿1丂偼娫堘偄側偔懳徧幃偵側傞丅
摨條偵
丂俴1丒俴2亄俴1丒俴3亄俴1丒俴3亖俿2
丂俴1丒俴2丒俴3亖俿3
偲慡偰婎杮懳徧幃偵側傞偺偱丄學悢偱昞偡偙偲偑偱偒傞丅
偙偺俁偮偺幃偼嶰師曽掱幃偺崻偲學悢偺娭學側偺偱丄俴1丆俴2丆俴3傪夝偲偡傞嶰師曽掱幃傪嶌傞偙偲偑偱偒傞丅
丂(倃亅俴1)(倃亅俴2)(倃亅俴3)亖侽
丂倃3亅(俴1亄俴2亄俴3)倃2亄(俴1俴2亄俴1俴2亄俴2俴3)倃亅俴1丒俴2丒俴3亖侽
偡偱偵嶰師曽掱幃偼夝偔偙偲偑偱偒偨偺偱丄俴1丆俴2丆俴3偑媮傑傞丅
俴1丆俴2丆俴3偑媮傑傟偽丄併傪偲偭偰丄
丂(倎亄倐)亅(們亄倓)亖併俴1乮偙傟偼學悢偺幃側偭偰偄傞乯
丂(倎亄們)亅(倐亄倓)亖併俴2
丂(倎亄倓)亅(倐亄們)亖併俴3丂偙傟偵
丂倎亄倐亄們亄倓亖亅倫
傪壛偊傟偽丄偙偺楢棫曽掱幃傪夝偔偙偲偑偱偒丄倎丆倐丆們丆倓傪媮傔傞偙偲偑偱偒傞丅
丂丂俀乮倎亄倐乯亖併俴1亅倫
丂亄俀乮倎亅倐乯亖併俴2亅併俴3丂丂
丂丂丂丂丂丂係倎亖併俴1亄併俴2亄併俴3亅倫
丂丂丂丂丒丒丒
寁嶼偡傞偺偑戝曄側偩偗偱丄棟孅偼嶰師曽掱幃傛傝傕娙扨偐傕偟傟側偄丅
俈丄巐師曽掱幃偼側偤夝偗傞偺偐
嶰師曽掱幃偼擇師曽掱幃偵抲偒姺偊丄巐師曽掱幃偼嶰師曽掱幃乮偮傑傝擇師曽掱幃乯偵抲偒姺偊偰夝偔偙偲偑偱偒偨丅
偦傟偑偱偒偨偺偼懳徧幃偺偍偐偘偱偁傞丅
偟偐傕丄偦偺懳徧幃偑偦傟偧傟偺師悢傛傝傕堦偮彮側偄悢偵側傞偐傜偱偁傞丅
S丗偮傑傝丄巐師曽掱幃偼丄擇師曽掱幃傪夝偄偰3併傪偲傝丄偝傜偵併傪偲傞傫偩偹丅
偙傟傪崻偺抲姺孮偱峫偊傞偲丄嶰師曽掱幃偺応崌偼俁偮偺崻偺抲姺偼俁師偺懳徧孮
乮俁屄偺抲偒姺偊偼俇偮偺尦偺孮乯偵側傞丅
巐師曽掱幃偺応崌偼係師偺懳徧孮乮係屄偺抲偒姺偊偼俀係屄偺尦偺孮亖俽4乯偩丅
孮偲偄偆偺偼丄墘嶼偵暵偠偰偄偰丄扨埵尦偲媡尦偑偁傞傕偺丅偝偭偒偺昞偼俁師偺懳徧孮俽3偩丅
巹偨偪偺恎偺傑傢傝偵偼偙偺孮偵側傞傕偺偑偨偔偝傫偁傞丅
懳徧孮偲偄偆偙偲偐傜僀儊乕僕偱偒傞傛偆偵丄懳徧側傕偺偼懳徧孮傪側偟偰偄傞丅
曽掱幃偱偄偆偲崻偺抲姺偼孮傪側偟偰偄傞丅偦偺懳徧孮偑崻崋傪庢傞偨傃偵懳徧惈傪曵偟偰偄偒晹暘孮偑彫偝偔側偭偰偄偔丅
丂丂丂丂丂丂丂丂丂懱丂丂丂丂孮
丂丂桳棟悢亖俻丂丂仜丂丂丂丂仜丂巐師曽掱幃偺懳徧孮亖俽4
丂丂丂丂丂丂丂丂丂乥丂丂丂丂乥丂丂嶰師曽掱幃偵偡傞
丂丂丂丂丂丂丂丂丂乥丂丂丂丂乥丂丂擇師曽掱幃偵偡傞
丂丂俻(併俢)亖俵丂仜丂丂丂丂仜丂併傪偲傞亖嬼抲姺偱曄傢傜側偄
丂丂丂丂丂丂丂丂丂乥丂丂丂丂乥丂丂俙4亖岎戙孮
丂丂丂丂丂丂丂丂丂乥丂丂丂丂乥
丂丂俵(3併俼)亖俶 仜丂丂丂丂仜丂3併丂傪偲傞
丂丂丂丂丂丂丂丂丂乥丂丂丂丂乥丂丂嘪4亖僋儔僀儞偺巐尦孮
丂丂俶(併俴)丂丂丂乥丂丂丂丂乥丂併傪偲傞
丂丂丂丂丂丂丂丂丂仜夝偗偨両仜丂乷倕乸
S丗曽掱幃傪夝偔偲偄偆偙偲偼丄n併乮檖崻乯傪晅偗懌偟偰偄偔偙偲側傫偩偹丅
S丗懱偲孮偑枾愙偵偮側偑偭偰偄傞偙偲傕傢偐偭偨丅
僈儘傾偼曽掱幃偵懳墳偟偨孮偑偁傞偲峫偊偨丅偦傟傪僈儘傾孮偲尵偆丅
偒偪傫偲偟偨掕媊傪偡傞慜偵丄戝傑偐側僀儊乕僕傪扵偭偰傒傛偆丅
偦偺偨傔偵僈儘傾孮傪嬶懱揑側曽掱幃偵偮偄偰峫偊偰傒傛偆丅
俉丄嬶懱揑側曽掱幃偺僈儘傾孮乧擇崁曽掱幃偺夝偒曽
丂倃5亅侾亖侽丒丒丒(1)丂崻偼侾偺俆忔崻偱偁傞丅
丂倃5亅侾傪乮倃亅侾乯偱妱傞偲丄乮俻偱婛栺偵偡傞乯
丂倃4亄倃3亄倃2亄倃亄侾亖侽丒丒丒(2)偑弌偰偔傞丅
偙偺曽掱幃傪僈儘傾孮傪梡偄偰夝偄偰傒傛偆丅
巐師曽掱幃偩偐傜俇偱傗偭偨傛偆偵偡傟偽夝偗傞偺偩偑丄偙偺曽掱幃偼傕偭偲娙扨偵夝偗傞丅
僈僂僗暯柺偱僆僀儔乕偺岞幃傪巊偊偽娙扨偩偑戙悢揑偵夝偔丅
側偍丄偙偺晹暘偼徣棯偟偰捈愙俴1偲俴2傊峴偭偰傕戝忎晇丅
傑偢丄尨巒俆忔崻傪冊偲偡傞偲丄(1)偺崻偼冊丆冊2丆冊3丆冊4丆冊5亖侾
(2)偺崻偼冊丆冊2丆冊3丆冊4偲偐側傝尷掕偝傟傞丅
偙偺崻偺抲姺偼孮偲側傞偼偢丅
丂冊仺冊2丂偲偡傟偽丄懠偺崻偺峴偔愭傕昁慠揑偵寛傑傞丅
丂冊仺冊2丂冊2仺冊4丂冊3仺冊6亖冊丂冊4仺冊8亖冊3丒丒丒(1243)
埲壓摨條偵丄
丂冊仺冊3丂冊2仺冊丂冊3仺冊4丂冊4仺冊2丒丒丒(1342)
丂冊仺冊4丂冊2仺冊3丂冊3仺冊2丂冊4仺冊丒丒丒(14)(23)
偙傟偼丄俽4偺晹暘孮偵側偭偰偄傞丅
孮偺昞傪嶌傞偲丄
丂丂丂丂丂乥丂丂倕丂丂 (1243)丂丂(14)(23)丂(1342)
丂丂倕丂丂乥丂丂倕丂丂 (1243)丂丂(14)(23)丂(1342)
丂(1243)丂乥丂(1243)丂 (14)(23)丂(1342)丂丂丂倕
丂(14)(23)乥 (14)(23)丂(1342)丂丂倕丂丂丂丂(1243)
丂(1342)丂乥丂(1342)丂丂丂倕丂丂丂(1243)丂 (14)(23)丂
(1243)亖冃偲偡傞偲丄(14)(23)亖冃2丄(1342)亖冃3偲側傞丅
冃偱傑偲傔傞偲丄
丂丂丂丂 乥丂倕丂丂冃丂丂冃^2丂冃^3丂
丂丂倕丂 乥丂倕丂丂冃丂丂冃^2丂冃^3
丂丂冃丂 乥丂冃丂丂冃^2丂冃^3丂倕
丂丂冃^2 乥丂冃^2丂冃^3丂倕丂丂冃
丂丂冃^3 乥丂冃^3丂倕丂丂冃丂丂冃^2
係崻偺抲姺偼俀係捠傝乮係丒俁丒俀丒侾亖俀係乯偁傞偑丄偙偺曽掱幃偺応崌偼係捠傝偵側偭偰偟傑偭偨丅
乷倕丆 冃丆冃2丆冃3乸亖俙偲偄偆埵悢係偺弰夞孮乮倅4偵側傞丅乯
乮偙偙傑偱偼崻傪媮傔傞偙偲偲偼捈愙偼娭學側偄偑丄崻偺抲姺孮偺椺偲偟偰偁偘傞乯
偙偺孮偺晹暘孮偼丄乷e乸偲乷倕丆冃2乸偺俀偮丅
乷倕丆冃2乸偼係忔偑婲偙偡抲姺偱惓婯晹暘孮乮偙傟偼廳梫側晹暘孮偱丄徻偟偔偼俋偱愢柧乯
偙偺抲姺冃2亖(14)(23)偱丄係崻偼師偺傛偆偵
{冊丆冊4乸偲乷冊2丆冊3乸偺俀偮偵暘椶偱偒傞丅
冃乮冊丆冊4乯亖冊2丆冊3丂丂冃2乮冊丆冊4乯亖冊丆冊4丂丂冃3乮冊丆冊4乯亖冊2丆冊3
冃乮冊2丆冊3乯亖冊丆冊4丂丂冃2乮冊2丆冊3乯亖冊2丆冊3丂丂冃3乮冊2丆冊3乯亖冊丆冊4
偩偐傜丄偦傟偧傟傪懌偟偰丄
丂俴1亖冊亄冊4
丂俴2亖冊3亄冊2
偲抲偒丄愊偲榓傪嶌傞偲冃,冃2,冃3偱抣偼曄傢傜側偄忋偵偦偺悢抣傕傢偐傞丅
丂俴1亄俴2亖冊亄冊2亄冊3亄冊4亖亅侾
丂俴1丒俴2亖冊亄冊2亄冊3亄冊4亖亅侾
傛偭偰丄擇師曽掱幃丂倲2亄倲亅侾亖侽傪夝偗偽丄俴1,俴2偑媮傑傞丅
丂俴1亖(亅侾亄併俆)乛俀
丂俴2亖(亅侾亅併俆)乛俀
偮傑傝丄冊亄冊4亖(亅侾亄併俆)乛俀丂丂冊丒冊4亖侾
丂丂丂丂冊3亄冊2亖(亅侾亅併俆)乛俀丂丂冊3丒冊2亖侾
摨條偵擇師曽掱幃丂倲2亅{(亅侾亄併俆)乛俀}倲亄侾亖侽
傪夝偗偽冊偲冊4偑媮傑傞丅
丂冊亖{亅(亅侾亄併俆)乛俀}亇併[{亅(亅侾亄併俆)乛俀}2亅係]丒丒丒(3)
冊2偲冊3傕摨偠傛偆偵媮傑傞丅偮傑傝丄併傪擇夞偲傟偽崻偑尒偮偐傞丅
乷倕丆冃丆冃2丆冃3乸偑曽掱幃(2)偺僈儘傾孮偱偁傞丅
崱傑偱僈儘傾懳墳偼忋偐傜壓傊偲彂偄偰偒偨偑丄崱搙偼媡偵彂偔丅
丂丂丂丂丂丂丂丂丂丂懱丂丂丂丂孮
丂丂丂俶乮(3)偺併乯 仜丂丂丂丂仜丂乷倕乸
丂丂丂丂仾併傪偲傞丂乥丂丂丂丂乥丂丂
丂丂擇師曽掱幃傪夝偔乥丂丂丂丂乥丂丂仾晹暘孮
丂丂丂俻乮併俆)亖俶 仜丂丂丂丂仜乷倕丆冃2乸
丂丂丂丂仾併傪偲傞丂乥丂丂丂丂乥丂嬼抲姺偱曄傢傜側偄(冊4+冊丆冊3+冊2偺抣偼冃2偱曄傢傜側偄)
丂丂擇師曽掱幃傪夝偔乥丂丂丂丂乥丂丂仾晹暘孮
丂丂丂俻=桳棟悢 丂丂仜丂丂丂丂仜乷倕丆冃丆冃2丆冃3乸
(冊4+冊3+冊2+冊=-1偼冃丆冃2丆冃3偱曄傢傜側偄)
偙偺曽朄偼倃7亅侾亖侽偱傕摨偠傛偆偵巊偊偰丄嵟弶擇師曽掱幃傪夝偒丄師偵嶰師曽掱幃傪夝偄偰崻傪媮傔傞偙偲偑偱偒傞丅
俇師曽掱幃偑戙悢揑偵夝偗偰偟傑偆偙偲偑嬃偒偩丅
傕偭偲傕丄僈僂僗偼侾俋嵨偺偁傞挬丄倃17亅侾亖侽偺戙悢揑側夝偒曽乮併偩偗傪巊偆乯傪媮傔傞曽朄傪巚偄偮偄偨偲偄偆偐傜偡偛偄丅
偦偆偄偊偽丄僈儘傾傕僈儘傾棟榑傪憂偭偨偺偑悢妛傪妛傃巒傔偰俁擭栚偺侾俈乣俉嵨偩偭偨丅
倃17亅侾亖侽偺僈儘傾孮偼丄僄僋僙儖偱寁嶼偟偨曽偑娙扨偱偁傞丅亂僄僋僙儖僨乕僞亃
偙偺孮傪尒傞偲丄偳偆偄偆孮側傜曽掱幃偑夝偗傞偺偐偑傢偐偭偰偔傞丅
崱搙偼曽掱幃偺僈儘傾孮偩偗偱側偔丄懳墳偡傞拞娫懱傕挷傋偰傒傛偆丅
俋丄曽掱幃偺僈儘傾孮亖奼戝懱偺倠亅帺屓摨宆孮
傕偭偲嬶懱揑側曽掱幃偺僈儘傾孮傪挷傋偰傒傛偆丅
偦偟偰僈儘傾孮偲奼戝懱偺娭學傪挷傋偰傒傛偆丅
丂(1)丂倃2亄俁倃亄侾亖侽
偙偺曽掱幃偺崻偼倃亖亅1.5亇0.5併俆
偩偐傜丄桳棟悢偩偗偺悽奅偺拞偱偼夝偔偙偲偑偱偒側偄丅
偱傕丄桳棟悢偵併俆傪壛偊偨悽奅偱偼夝偔偙偲偑偱偒傞丅
桳棟悢偵併俆傪壛偊偨悽奅偼丄桳棟悢偲併俆偱偱偒偨悽奅偱偁傞丅
偙傟傪俻(併俆)偲昞偟丄俻乮桳棟悢乯傪奼戝偟偨悢偺悽奅乮懱乯偲偄偆丅
偙偺悽奅偺悢偼倎亄倐併俆偲昞偝傟丄巐懃偼偡傋偰惉傝棫偮丅
偙偺悽奅乮亖俻(併俆)乯偱偼丄曽掱幃(1)偼
丂{倃亅(亅1.5亄0.5併俆)}{倃亅(亅1.5亄0.5併俆)}亖侽
偲場悢暘夝偱偒傞乮夝偔偙偲偑偱偒傞乯丅
崻傪抲姺偡傞偙偲乮兛佁兝乯偼丄俻乮併俆乯偺悽奅偱尒傞偲偳偆偄偆堄枴傪帩偭偰偄傞偐偲偄偆偲丄
俻乮併俆乯偐傜俻乮併俆乯傊偺帺屓摨宆幨憸冃丗併俆仺亅併俆丂乮偨偩偟桳棟悢偼堦愗曄偊側偄乯偵偁偨傞丅
偙偺幨憸偼崻偺抲姺偵偁偨傝丄冃偼兛仺兝偲側傝丄偙偺幨憸傪擇夞孞傝曉偡偲乮冃2乯丗兛仺兛偲側傞丅
偮傑傝埵悢俀偺孮偲側傞丅
S丗寢嬊幨憸偲抲姺偼摨偠偙偲偵側傞偺偱偡偹丅
T丗偦偆丄抲姺孮偲帺屓摨宆幨憸偺孮偼摨宆丅偦偟偰偙偺幨憸偼桳棟悢偺悽奅偺曽掱幃(1)傪曄偊側偄丅
傕偆堦偮椺傪偁偘傛偆丅
丂(2)丂丂倃2亅俆倃亄俇亖侽
倃亖俀丆俁丂偱偁傞偑丄偙傟偼抲姺偱偒側偄丅曽掱幃偼曄傢傜側偄偑丄偦傕偦傕偙偺曽掱幃偼桳棟悢偱暘夝偱偒傞丅
丂(倃亅俀)(倃亅俁)亖侽
偲側傝丄俀偲俁傪擖傟懼偊偰傕曽掱幃偼曄傢傜側偄偑丄
桳棟悢偺悽奅偱俀偲俁傪擖傟懼偊偨傜傔偪傖偔偪傖偵側偭偰偟傑偆丅
偮傑傝丄偙偺応崌偼桳棟悢偺悽奅偱偺抲姺偼偱偒側偄丅
偲尵偆偐抲姺偼慡偔摨偠傕偺傪摨偠傕偺傊堏偡峆摍幨憸偩偗偱偁傞丅
偙偺曽掱幃偺僈儘傾孮偼扨埵尦偩偗偺孮偱偁傞丅
S丗僈儘傾孮傪峫偊傞偲偒偵偼婛栺曽掱幃偩偗傪庢傝埖偆傫偱偡偹丅
T丗偳偺懱偱婛栺偐偑戝帠偲偄偆偙偲偱偡偹丅
偝傜偵嶰師曽掱幃偱峫偊偰傒傛偆丅
丂(3)丂丂倃3亅侾亖侽偼偳偆側傞偐丅
丂(倃亅侾)(倃2亄倃亄侾)亖侽偲場悢暘夝偱偒傞丅乮兛亖侾乯
偙偺抜奒偱丄塃懁偺幃偱崻兝偲兞傪擖傟懼偊偰傕俻偺悽奅傪曄偊傞偙偲偼側偄丅偨偩偟丄侾偲兝傗兞偲抲偒姺偊傞偙偲偼偱偒側偄丅
抲姺孮偱偄偆偲丄乽曄偊側偄乿偲乽兝偲兞傪抲偒姺偊傞乿抲姺偺傒偺埵悢俀偺孮偵側傞丅
偙偺曽掱幃傪偝傜偵場悢暘夝偡傞偨傔偵丄併(亅俁)傪晅偗壛偊丄俻(併(亅俁))亖俻乮冎乯偲偄偆悽奅傪偮偔傞丅
俻(併(亅俁))亖乷倎亄倐併(亅俁)丗倎丆倐併俻}
偙偺悽奅偱偼丄(3)偼丂(倃亅侾)(倃亅冎)(倃亅冎2)亖侽偲場悢暘夝偱偒傞丅
崻偼丄倃亖侾丆冎丆冎2 偱偁傞丅偙偺悽奅俻(併(亅俁))亖俻乮冎乯偱偼丄愭傎偳偺崻偺抲姺偼丄
俻(併(亅俁))偐傜俻(併(亅俁))傊偺帺屓摨宆幨憸偱丄
冃丗併(亅俁)仺亅併(亅俁)乮桳棟悢偼曄偊側偄乯偲偄偆幨憸偵偁偨傞丅
抲姺孮偱偄偆偲丄兝偲兞傪抲偒姺偊傞抲姺冃偲扨埵尦倕偐傜偱偒偰偄傞丅
冃亊冃亖倕偵側偭偰偄傞偟丄併(亅俁)傪亅併(亅俁)偵曄偊偰傕悽奅偺巐懃偼柕弬偟側偄丅
偩偐傜丄偙偺曽掱幃偺僈儘傾孮偼乷倕丆冃}偱偁傞丅
偙偺傛偆偵丄崻偺抲姺偲懱偺幨憸偲偺娫偵枾愙側娭學偑偁傞偺偱偼側偄偐偲姶偠傞丅
僈儘傾偼崻偺抲姺傪怺偔捛媦偟偰丄偦傟偑奼戝偝傟偨懱偺帺屓摨宆幨憸偵偁偨傞偲偄偆偙偲傪敪尒偟偨丅
乮幚偼偙傟傪偼偭偒傝偝偣偨偺偼僈儘傾偱偼側偔僨僨僉儞僩丅僈儘傾偼崻偺抲姺偲奼戝懱偲偺懳墳傪尒偮偗偨乯
丂(4)丂丂倃3亅俀亖侽
偙偺曽掱幃偺僈儘傾孮偼曽掱幃傪尒偨偩偗偱偼傢偐傜側偄丅
傑偢丄嶰師曽掱幃偩偐傜俽3偺晹暘孮偩傠偆丅
愭偵俁崻傪弌偟偰傒傞偲丄3併俀丆3併俀冎丆3併俀冎2偱偁傞丅
冎傪偐偗傞偙偲偵傛傞弰夞抲姺(123),(132)偼峫偊傜傟傞丅
偱偼丄屳姺偼偳偆偩傠偆偐丅3併俀冎丆3併俀冎2偺抲姺(23)偼惉傝棫偪偦偆丅
晹暘孮偳偆偟偺偐偗嶼偲妱傝嶼乧惓婯晹暘孮偲忚梋孮
幚偼偙偺栤戣偼擸傫偱偟傑偭偨丅
(123)丆(132)丆(23)偱孮偑偱偒傞偺偩傠偆偐丠
乷倕丆(123)丆(132)乸偼孮丅乷倕丆(23)乸傕孮偩丅偙傟傪崌懱偝偣偨傜偳偆側傞偐丅
孮偳偆偟偺偐偗嶼偩丅偦傟偧傟偺尦傪偐偗傞偲弌偰偔傞丅偪傖傫偲俇尦偵側傞丅
丂乷倕丆(123)丆(132)乸亊乷倕丆(23)乸亖乷倕丆(123)丆(132)丆(23)丆(23)(123)丆(23)(132)乸
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖乷倕丆(123)丆(132)丆(23)丆(12)丆(13)乸丂乮佹(23)(123)亖(12)丆(23)(132)亖(13)乯
寢嬊俽3偲摨偠偩丅丂乮孮偼壜姺偲偼尷傜側偄偺偱嵍塃擖傟懼偊偨偺傕妋偐傔傞昁梫偑偁傞乯
偝傜偵丄
丂乷倕丆(123)丆(132)乸亊乷倕丆(12)乸亖乷倕丆(123)丆(132)丆(12)丆(12)(123)丆(12)(132)乸
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂亖乷倕丆(123)丆(132)丆(12)丆(13)丆(23)乸
偙偺偐偗嶼傕摨偠寢壥偵側傝丄孮偳偆偟偺偐偗嶼偑偱偒傞偙偲偑傢偐傞丅
偦偆偡傞偲丄孮偺妱傝嶼傕峫偊傜傟傞偺偱偼側偄偐丅
偱傕丄
丂乷倕丆(123)丆(132)丆(23)丆(23)(123)丆(23)(132)乸乛乷倕丆(123)丆(132)乸亖乷倕丆(23)乸
偲宍幃揑偵峫偊偰傕怴偟偄堄枴偼弌偰偙側偄丅偙傟偑堄枴傪帩偮偨傔偵偼偳偆峫偊偨傜偄偄偺偐丠
偙偙偱乷倕丆(123)丆(132)乸亖俙丆乷倕丆(23)乸亖俛偲偍偔丅
乷倕丆(123)丆(132)丆(23)丆(23)(123)丆(23)(132)乸亖乷俙丆(23)俙乸乧(1)
偙偺傑偲傔偨俙偲(23)俙偑孮偵側傟偽怴偟偄孮偑惗傑傟偨偙偲偵側傞丅昞偱帋偟偰傒傛偆丅
丂丂丂丂丂乥丂俙丂 丂丂(23)俙丂_
丂丂丂丂俙乥丂俙丂丂丂俙(23)俙丂丂丂
丂丂(23)俙乥(23)俙丂(23)俙(23)俙丂
偙偺偲偒丄俙亊俙亖俙側偺偱丄(23)俙亖俙(23)偩偭偨傜丄
丂丂丂丂丂乥丂俙丂 丂丂(23)俙
丂丂丂丂俙乥丂俙丂丂丂 (23)俙丂丂丂
丂丂(23)俙乥(23)俙丂丂丂俙丂
偲側偭偰丄俙傪扨埵孮偲偡傞孮偵側傞丅
妋偐傔偰傒傞丅
(23)俙亖{(23),(12),(13)}, 俙(23)={(23),(13),(12)}偱摨偠丅
偮傑傝丄俙傪扨埵孮偲偡傞怴偟偄孮偑惗傑傟偨偙偲偵側傞丅
偱偼丄
丂乷倕丆(23)丆(123)丆(123)(23)丆(132)丆(132)(23)乸乛乷倕丆(23)乸亖乷俛丆(123)俛丆(132)俛乸乧(2)
偼惉傝棫偮偺偩傠偆偐丅
傕偆梊憐偑偮偔偲巚偆偗偳丄惉傝棫偨側偄丅
妋偐傔偰傒傛偆丅丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂佀丂傕偟丄(123)俛=俛(123),(132)俛=俛(132)偩偭偨傜丄
丂丂丂丂丂 乥丂俛丂 丂丂丂(123)俛丂丂丂丂丂(132)俛 _丂丂 丂丂俛丂丂(123)俛丂(132)俛
丂丂丂丂 俛乥丂俛丂丂丂丂俛(123)俛丂丂丂丂俛(132)俛丂丂丂丂丂俛丂丂(123)俛丂(132)俛
丂丂(123)俛乥(123)俛丂(123)俛(123)俛丂(123)俛(132)俛丂丂丂(123)俛丂(132)俛丂丂俛
丂丂(132)俛乥(132)俛丂(132)俛(123)俛丂(132)俛(132)俛丂丂丂(132)俛丂丂俛丂丂 (123)俛
偲偙傠偑丄{倕,(23)}亊(123)={(123),(12)}乧(3)丂丂(123)亊{倕,(23)}={(123),(13)}乧(4)
摨偠偱偼側偄丅偟偨偑偭偰孮偵偼側傜側偄丅
偮傑傝丄俙偱偼傢傝嶼偱偒傞偗偳俛偱偼偱偒側偄丅
偪側傒偵俙偼俁師偺岎戙孮偲尵偄俙3偱昞偡丅
丂丂乷e俙3丆(23)俙3乸亖乷俙3e丆俙3(23)乸亖俽3乛俙3丂丂乮(23)偼(12)傗(13)偲抲偒姺偊偰傕摨偠乯
偮傑傝丄妱傝嶼偑偱偒傞孮偲丄偦偆偱側偄孮偑偁傞偲偄偆偙偲偩丅
偙偺妱傝嶼偑偱偒傞孮傪惓婯晹暘孮偲偄偆丅
偦偟偰丄妱傝嶼偟偰偱偒偨孮傪忚梋孮乮彜孮乯偲偄偆丅
孮偵側傞偐側傜側偄偐偺棟桼偼丄(2)偺応崌偼丄塃偐傜偐偗偨(3)偲嵍偐傜偐偗偨(4)偲偑堦抳偟側偄丅
偲偙傠偑丄(1)偺応崌偼尒帠偵堦抳偡傞偐傜偱偁傞丅
崱傑偱偵弌偰偒偨嬼抲姺偼慡偰惓婯晹暘孮偱偁傞丅
偦偟偰丄僈儘傾偼丄偙偺惓婯晹暘孮偑偮偔傞忚梋孮偑弰夞孮偱偁傞偙偲偑丄曽掱幃偑戙悢揑偵夝偗傞棟桼偱偁傞偙偲傪敪尒偟偨丅
拞娫懱偲晹暘孮乧僈儘傾偺懳墳
偝偰丄偙偺孮偼俽3偲摨偠偵側偭偰偟傑偭偨偑丄懱偺曽偱偼偳偆側偭偰偄傞偺偩傠偆偐丅
丂俻(3併俀丆冎)
亖乷倎1亄倎23併俀亄倎33併係亄倎4冎亄倎53併俀冎亄倎63併係冎丗倎i偼俻偺梫慺乸
丂丂丂丂丂乮佹丂俻乮3併俀乯乮冎乯亖乷倎1亄倎23併俀亄倎33併係乸亊乷倎1乫亄倎2乫冎乸乯
偙偺僈儘傾奼戝懱偼偙偺條偵俇師偱昞偝傟傞丅偮傑傝儀僋僩儖偺撈棫側婎掙偲摨偠丅
傑偨丄懳墳偡傞僈儘傾孮俽3偺埵悢傕俇偱偁傞丅偮傑傝丄埵悢偲師悢偼懳墳偟偰偄傞丅
(4)偺曽掱幃偼丄桳棟悢俻偺悽奅偱偼場悢暘夝偡傞偙偲偑偱偒側偄乮婛栺乯丅
暘夝偡傞偨傔偵偼丄冎傗3併俀傪晅偗壛偊丄俻偺悽奅傪奼戝偡傞昁梫偑偁傞丅
丂椺偊偽丄俻(3併俀)亖乷倎1亄倎23併俀亄倎33併係丗倎倝偼俻偺梫慺乸偲奼戝偟偰傒傛偆丅
偡傞偲丄
丂(倃亅3併俀)(倃2亄3併俀倃亄3併係)亖侽
偲暘夝偱偒傞丅偝傜偵丄俻乮3併俀乯偵冎傪晅偗懌偟偰丄
丂俻(3併俀丆冎)
亖乷倎1亄倎23併俀亄倎33併係亄倎4冎亄倎53併俀冎亄倎63併係冎丗倎倝偼俻偺梫慺乸
偲偡傟偽丄
丂(倃亅3併俀)(倃亅3併俀冎)(倃亅3併俀冎2)亖侽偲暘夝偱偒傞丅
乮幚偼偙偺摴嬝偼媡丅偙偺応崌3併俀偑傢偐偭偰偄傞偺偱場悢暘夝偟偨偑丄晛捠偼傢偐傜側偄丅
丂偦偙偱丄冎傪愭偵揧晅偟偰偐傜3併俀傪揧晅偟偰奼戝懱傪嶌偭偰夝偔丅乯
偙偺帪丄崻偺抲姺偲奼戝懱俻乮3併俀乯丆俻乮3併俀冎乯丆俻乮3併俀冎2乯偲偺娭學偼偳偆側偭偰偄傞偺偩傠偆偐丠
丂乮侾丂俀丂俁乯亖乮3併俀丂3併俀冎丂3併俀冎2乯丂偲偡傞丅
崻偺抲姺孮偼偡偱偵傢偐偭偰偄傞偑丄偦傟偵懳墳偡傞懱偺帺屓摨宆曄姺偼偳偆峫偊偨傜偄偄偺偐丠
傑偢冎傪偐偗傞偲偄偆曄姺冃傪峫偊偰傒傞丅
丂冃乮3併俀乯亖3併俀冎
丂冃乮3併俀冎乯亖3併俀冎2
丂冃乮3併俀冎2乯亖3併俀
偙傟偼抲姺乮侾俀俁乯偵偁偨傞丅丂
偱偼丄偙傟傪擇夞孞傝曉偡偲丄
丂冃2乮3併俀乯亖3併俀冎2
丂冃2乮3併俀冎乯亖3併俀
丂冃2乮3併俀冎2亖3併俀冎丂偙傟傜偼丄乮侾俁俀乯偵偁偨傞丅
師偼乮俀俁乯亖冄偵偁偨傞偺偼壗偩傠偆丠
偙傟偼冎偩偗傪曄偊偰丄3併俀偼曄偊側偄曄姺乮偮傑傝併(亅俁)仺亅併(亅俁)乯偱丄
丂冄乮3併俀乯亖3併俀
丂冄乮3併俀冎乯亖3併俀冎2
丂冄乮3併俀冎2乯亖3併俀冎
偲峫偊傞偙偲偑偱偒傞丅偦偟偰丄偙偺擇偮偺曄姺偺慻傒崌傢偣偱丄偝傜偵擇偮偺曄姺偑弌偰偔傞丅
丂冄冃乮3併俀乯亖3併俀冎2
丂冄冃乮3併俀冎乯亖3併俀冎
丂冄冃乮3併俀冎2乯亖3併俀丂丂偙傟傜偼乮侾俁乯
丂冃冄乮3併俀乯亖3併俀冎
丂冃冄乮3併俀冎乯亖3併俀
丂冃冄乮3併俀冎2乯亖3併俀冎2丂丂偙傟傜偼乮侾俀乯
偲偄偆傢偗偱丄孮偲懱偺曄姺偑妋掕偱偒偨丅
桳棟悢偺悽奅偱偼丄俁偮偺崻偺慡偰偺抲姺偵傛偭偰曽掱幃(4)偺抣偼曄傢傜側偄偺偱丄
抲姺孮偼俁両亖俁亊俀亖俇偺尦偑偁傞丅
孮昞偵偡傞偲丄乮123乯偼1仺2仺3仺1偲懼偊傞抲姺
丂丂丂丂 |丂倕丂 乮123乯 乮132乯乮12乯乮13乯 乮23乯
丂 丂倕丂|丂倕丂 乮123乯 乮132乯乮12乯乮13乯 乮23乯
丂乮123乯|乮123乯乮132乯丂 倕丂 乮23乯乮12乯 乮13乯
丂乮132乯|乮132乯丂 倕丂 乮123乯乮13乯乮23乯 乮12乯
丂乮12乯 |乮12乯丂乮13乯 乮23乯丂倕丂乮123乯乮132乯
丂乮13乯 |乮13乯丂乮23乯 乮12乯乮132乯 倕丂 乮123乯
丂乮23乯 |乮23乯丂乮12乯 乮13乯乮123乯乮132乯 倕
偝偭偒偺乷倕丆(23)乸偼偙偺孮偺晹暘孮偵側偭偰偄傞丅
丂丂丂 丂|丂倕乮23乯丂丂崻俀仺俁仺俀偵曄偊傞抲姺
丂丂倕 丂|丂倕乮23乯
丂乮23乯 |乮23乯倕
偱傕丄晹暘孮偼懠偵傕俁偮偁傞丅
丂丂丂 丂|丂倕乮12乯丂丂崻侾仺俀仺侾偵曄偊傞抲姺
丂丂倕 丂|丂倕乮12乯
丂乮12乯 |乮12乯倕
丂丂丂 丂|丂倕乮13乯丂丂崻侾仺俁仺侾偵曄偊傞抲姺
丂丂倕 丂|丂倕乮13乯
丂乮13乯 |乮13乯倕
丂丂丂丂 |丂 倕丂乮123乯乮132乯丂崻侾仺俀仺俁仺侾偵曄偊傞抲姺
丂丂 倕丂| 丂倕丂乮123乯乮132乯
丂乮123乯|乮123乯乮132乯丂 倕
丂乮132乯|乮132乯丂 倕丂乮123乯
偙傟傜偺晹暘孮偲拞娫懱偑帺慠偵懳墳偟偰偄傞偺偑傢偐傞丅
椺偊偽丄晹暘孮乷倕丆(23)乸亖乷倕丆冄乸偵懳墳偡傞拞娫懱偼丄偙偺曄姺偱曄傢傜側偄懱丄偮傑傝俻乮3併俀乯偲峫偊傞偙偲偑偱偒傞丅
摨條偵丄乷倕丆(13)乸亖乷倕丆冄冃乸偱曄傢傜側偄拞娫懱偼俻乮3併俀乯丅
乷倕丆(12)乸亖乷倕丆冃冄乸偱曄傢傜側偄拞娫懱偼俻乮3併俀冎2乯丅
丂擮偺偨傔偵丄俻(3併俀冎)亖乷倎亄倐3併俀冎丗倎丆倐偼俻偺梫慺乸偑奼戝懱偺堄枴丅
偙偺尦傪俀忔偡傞偲丄3併係冎2偱丄俁忔偡傞偲俀偲側傝丄3併俀傗3併俀冎2偼娷傑傟側偄丅
偙傟偲俻(3併俀冎2)偺擇偮偼堘偭偨悽奅乮懱乯偲偄偆偙偲偩丅
偝偰丄栤戣偼乷 倕丆乮123乯丆乮132乯乸亖乷倕丆冃丆冃2乸偱曄傢傜側偄拞娫懱俻乮丠乯偼壗偩傠偆偐丠
偦偺慜偵丄俽3偵懳墳偡傞偺偼俻乮3併俀丆3併俀冎丆3併俀冎2乯偩偗偳丄
偙傟偼愭偵傗偭偨傛偆偵丄俻(3併俀丆冎)偲偄偆奼戝懱偱偁傞丅
偦偟偰丄偙偺悽奅偺帺屓摨宆曄姺偼俽3偲摨宆偱偁傞丅
丂偝偰丄乮侾俀俁乯偼冎傪偐偗傞偲偄偆曄姺偩偭偨丅偦偙偱師偺奼戝懱傪峫偊偰傒傞丅
丂俻(冎)亖乷倎亄倐冎丗倎丆倐偼俻偺梫慺乸
偙偺悽奅偱偼冎傗冎2偑偁傝丄亊冎傗亊冎2偱曄傢傜側偄乮冎仼仺冎2乯丅
偮傑傝丄(123)偲(132)偱曄傢傜側偄懱偱偁傞丅偟偐傕丄奼戝懱俻(3併俀丆冎)偺晹暘懱偱偁傞丅
偙偺條偵俽3偺係偮偺晹暘孮偵傛偭偰晄曄側晹暘懱乮俻偺奼戝懱乯偑偁偭偰尒帠偵懳墳偟偰偄傞丅
恾偱傑偲傔偰傒傞偲丄

偳偆偩傠偆偐丅
奼偘傜傟偨悽奅乮奼戝懱乯偺曄姺偲崻偺抲姺孮偲偑懳墳偟偰偄傞偙偲丄
峀偘傜傟偨悽奅乮拞娫懱乯偲抲姺孮偺晹暘孮偑懳墳偟偰偄傞偙偲偑偍傏傠偘側偑傜僀儊乕僕偱偒偰偒偨偩傠偆偐丅
係師曽掱幃偱傗偭偰傒傞偲丄偙偺懳墳偑傛傝嫮偔姶偠傜傟傞丅
偙偺懳墳傪僈儘傾懳墳偲偄偆丅
偦偟偰偙偺懳墳偼丄偳傫側悽奅偺奼戝偵傛偭偰曽掱幃偑夝偗傞偺偐傪巜帵偟偰偔傟傞丅
偦傟偼丄暋嶨側懱乮曽掱幃乯偺峔憿傪傢偐傝傗偡偄孮偵抲偒姺偊偰媍榑偡傞偲偄偆夞傝摴偺抭宒側偺偩丅
懕偒佀亂僈儘傾棟榑乧壜夝孮偺敪尒丂僕僋僜乕僷僘儖偺嵟屻偺僺乕僗亃傊
丂丂丂丂丂栚師傊傕偳傞
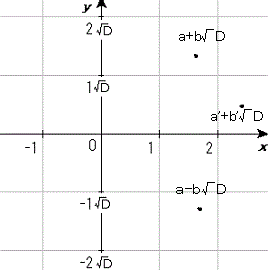 偙偺暯柺乮倎亄倐併俢偺悽奅乯偼丄倃幉偵懳偟偰懳徧偵側偭偰偄傞丅
偙偺暯柺乮倎亄倐併俢偺悽奅乯偼丄倃幉偵懳偟偰懳徧偵側偭偰偄傞丅