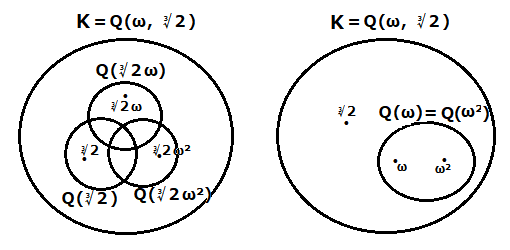ガロア理論・・・可解群の発見
ジクソーパズルの最後のピース
1、はじめに
これまでの学習で、正則拡大体の中間体とガロア群の部分群の間には一対一の対応があることが直観的につかめたと思う。
次の課題を確認しておこう。
(1) 正規部分群はなぜ考えられたのか?⇒「中学生にもわかるガロア理論の試み」で説明
(2) 方程式が解けることは群の方ではどう表されるのか?⇒可解群はどうやって発見されたのか?
(3) 体の具体的なイメージ(方程式が解ける道筋)。
特に、可解群はガロア理論の最後のピースと言える。
例によって、具体的な方程式χ3−2=0を使ってその拡大体と部分群を探りながら、可解群のイメージを育てていきたい。
2、χ3−2=0 を解く
この方程式の(正則拡大体の)中間体と(ガロア群の)部分群は前に取り上げた。
ここでは、この方程式の解き方をたどりながら、この(ガロアの)対応をもっと詳しく調べてみよう。
まずこの方程式は3次方程式なので、復習を兼ねて3次方程式の解き方で解いてみよう。
根をα,β,γとすると、
χ3−(α+β+γ)χ2+(αβ+βγ+γα)χ−αβγ=0
最初に分解式を作る。
L1=α+β+γ=0
L2=α+βω+γω2
L3=α+βω2+γω
この時点で拡大体はQ(ω)ということ。(ω2はωによって生み出され共役)
もっと言えば、Q(ω)の中で必ず対称式ができる。
L23・L33=0
L23+L33=2(α+β+γ)3−9(α+β+γ)(αβ+βγ+γα)+27αβγ=27×2
L23とL33を根とする2次方程式を作ると、簡単に因数分解できる。
(L23)2−27×2(L23)=0
L23(L23−27×2)=0
L23=0,L33=27×2
三乗根をとって、
L1=α+β+γ=0・・・(1)
L2=α+βω+γω2=0・・・(2)
L3=α+βω2+γω=33√2・・・(3)
この時点でQ(ω)に3√2を添付した拡大体となる(元素は下の図2の通り)。
つまり、3乗すればQ(ω)の中で対称式ができる。⇒根を求めるためには3乗根をとる。
この3式を加えると、α=3√2。
これを(1)に代入してβを求めると、β=−γ−3√2
(2)に代入すると、γ=3√2(ω2-1)/(ω-ω2)=3√2ω。だからβ=3√2ω2
α=3√2,β=3√2ω2,γ=3√2ω
ちなみにこの3根のイメージ。根の位置はガウス平面で。係数は有理数。
この図を見ると、根の置換群の位数が6であることがわかります。
この正三角形の回転や対称の移動がそのまま置換群になります。
さらに他の三次方程式の根でも確かめてみましょう。これはωとω2。
ついでに係数が有理数の4次方程式の根。
(X4+2=0にすると、この方程式のガロア群が位数8であることが図からわかってしまいます。4根が正方形を描きます。)
これらを見ると方程式の根の対称性がよくわかる。
さらに五次方程式の根などを見るには【体論への誘い】のページへ
3、χ3−2=0の根の拡大体(正則拡大体)
このような道筋で根を求めることができた。
ではどんな拡大体だったら根を求めることができるのか、どんな拡大体なら根が求まらないのかを調べてみよう。
まずこの3根でQの拡大体を作ってみよう。
Q(3√2),Q(3√2ω),Q(3√2ω2)という3つの体ができる。(これを共役な体という)
Q(3√2)は虚数ではないので他の2つの体と異なっている。
(つまり、Q(3√2)→Q(3√2ω)への同型対応は自己同型ではない)
だから、この3つの共役な拡大体だけではこの方程式は一次式に因数分解できない。
ではどのような拡大をしたら一次式に因数分解できる体になるか。
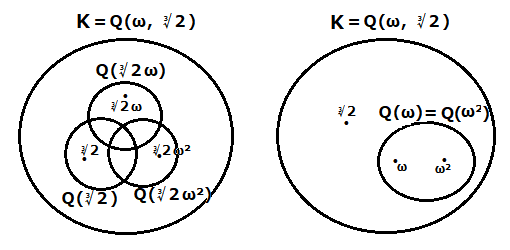
それは、Q(3√2,3√2ω,3√2ω2)=Q(3√2,ω)=Q(3√2+ω)である。
S:この拡大体って他にも考えられますよ。例えば、,Q(3√2ω+ω)はだめなんですか?
それは良い質問です。3つの根を使うとまだ他にも考えられますね。
S:Q(3√2ω2+ω),Q(3√2+ω2),Q(3√2ω+ω2),Q(3√2ω2+ω2)があります。
さて、この6つの拡大体をよく見ると、・・・
S:これらの拡大体は全て一致しますね。
S:混乱してきた。さっきの一つ一つの根の拡大では一致しなかったけど、この拡大は一致する。
S:ということは、この拡大体の自己同型写像(群)がきまる。
例えば(3√2+ω)→(3√2ω+ω)という対応を考えれば他のも自然に決まってきます。
すごいことに気がつきましたね。これはσ=(123)と同じですね。
この6つの拡大体の自己同型写像と根の置換群は完全に対応します。
S:どういうこと? わかりません。
この対応σは、σ(3√2)=3√2ωで、σ(ω)=ωだから、α→β→γ→αとなるから(123)と同じ。
(3√2+ω)→(3√2+ω2)は、τ(3√2)=3√2,τ(ω)=ω2だから(23)。
S:ということは、これらの6つの拡大体は根を添付した「共役体」であり、しかも一致する。
勇気のある人はこの6つを根とする方程式を展開してみてください。係数は全て有理数になるはずです。
ちなみに、3√2+ωと3√2ω+ωと3√2ω2+ωを根とする方程式を展開すると、
χ3−3ωχ2+3ω2χ−3=0となり、係数がQ(ω)の方程式になります。
そうです。これはさっきの3根を添付して共役体が一致する最小の体です。
そしてこの体の中では先のように根を見つけることができます。
このようにすべての共役体が一致するとき「Qの正則拡大体(ガロア拡大体)」といいます。
上の図の違いは、左の3つの拡大体は異なっているが、右の拡大体Q(ω)とQ(ω2)は一致していること。
このように一致していると、Q(ω)の自己同型対応が考えられ、右側の拡大体Q(ω)=Q(ω2)もガロア拡大体であることがわかります。
S:共役体が一致していると自己同型群(ガロア群)があるから、それは根の置換で対称であり対称式で根が求まるということですね。
図でまとめてみると、
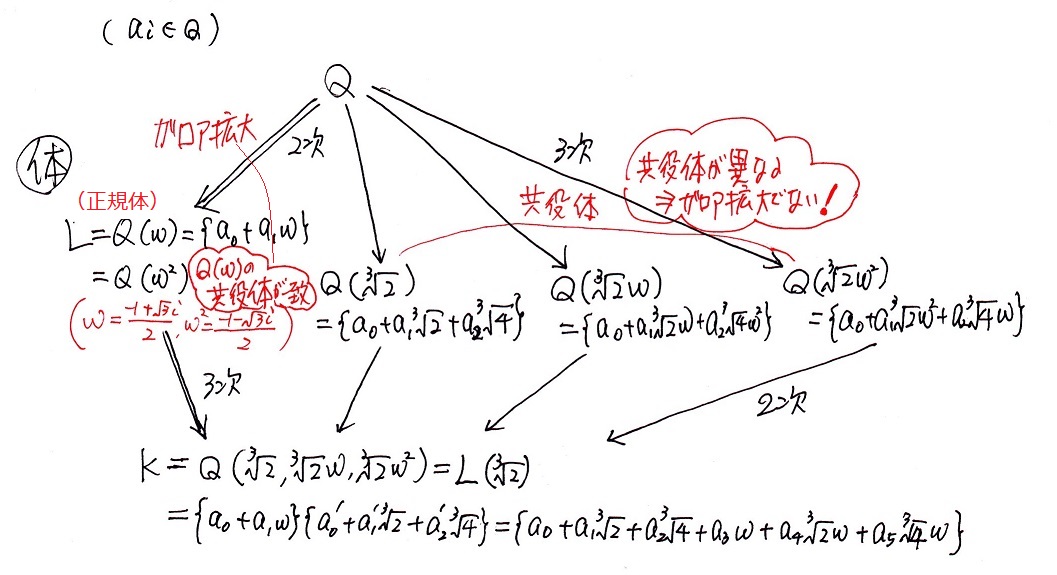
Q(3√2,3√2ω,3√2ω2)=L(3√2)=Q(3√2,ω)
=Q(3√2+ω)=Q(3√2ω+ω)=Q(3√2ω2+ω)=Q(3√2+ω2)
=Q(3√2ω+ω2)=Q(3√2ω2+ω2)

S:これらの図でいうと、さっきの方程式の解き方が左の二重線の中間体の列を通っているということ。
そして、それはガロア拡大になっているということだ。
そうですね。Q(ω)の方を見てみると、
Q(ω)の共役な体はQ(ω2)で一致するので(Q(ω)=Q(ω2):√の符号が変わる対応)ガロア拡大。
S:Kもガロア拡大だからこの拡大が方程式が解ける道筋なんですね。
こうやって2乗根や3乗根を付け足して体を拡大していくといつか方程式が一次式に因数分解できる体にたどり着く。
この道筋と他の道筋は何が違うのだろうか?
それはこの正則拡大体に対応するガロア群を調べることではっきりしてくる。
さっきのように体の方だけで議論しようとすると、とても複雑で計算が大変。
でも、ガロアの対応によってより分かりやすい群の方で議論できるはずというのがガロアの目論見。
このことをもっと詳しく調べてみよう。
体の拡大とガロア群について、拡大された中間体の元素(基数)の個数(次元)が決まってくることに注意。
S:中間体の次数と部分群の位数とがちゃんと対応している。
今度は部分群の方の図。
4、χ3-2=0 のガロア群とガロア拡大体(正則拡大体)の対応
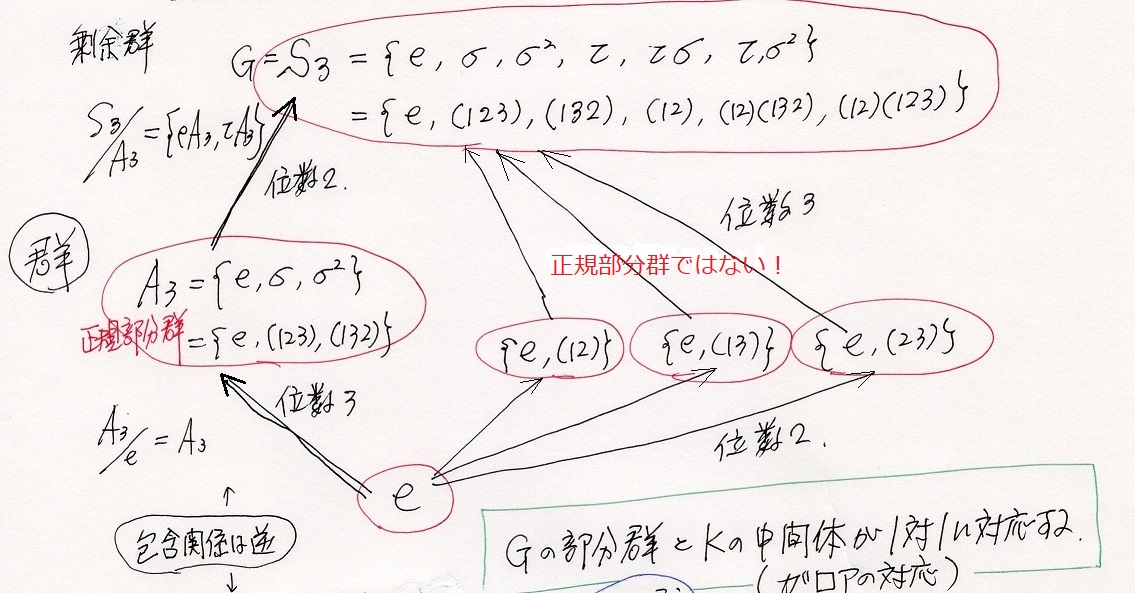
S:下の方に包含関係が逆と書いてあるけど?
これは体の方はQ<L<Kで群の方はS3>A3>{e}と包含の方向が逆になっていることを示しています。
(反変関手の例)
(注:上の中間体と対応する群は、Q(3√2)が{e,(23)}で、Q(3√2ω2)が{e,(12)}。eに{}を忘れた。)
さて、ここで中間体と部分群の間の対応をもっと調べてみよう。
さっきの図とは上下が逆だけど対応の図を示すと、
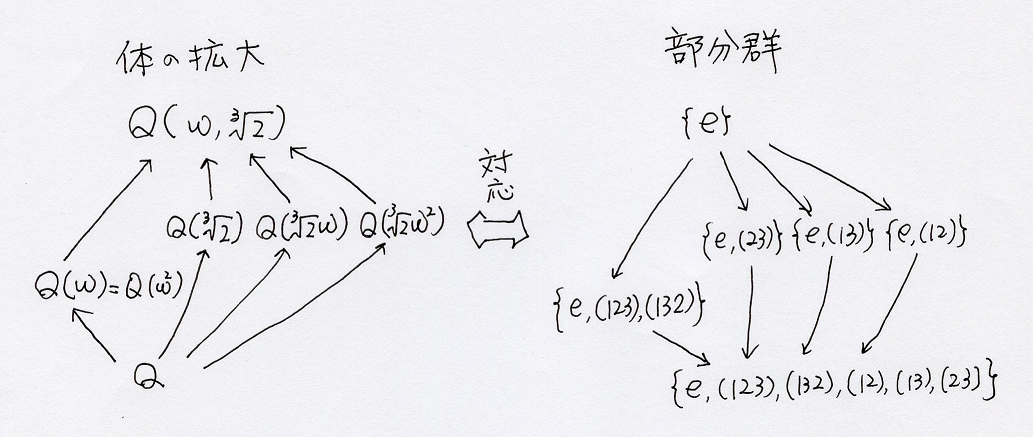
(L=Q(ω),K=L(3√2)=Q(ω,3√2), A3={e,(123),(132)},S4={e,(123),(132),(23),(12),(13)})
体の拡大の方にも元素(拡大体を生成する元素で、ベクトルの基底のようなもの)を対応させる同型対応が考えられて、
自己同型群が生まれる中間体があることに気がつく。
S:どの体を拡大したのかで自己同型群が異なってきますね。
S:例えば、KはQを拡大したものと考えると6元の拡大体になるし、
Lを拡大したと考えると3元の拡大になりますね。
このとき、何を動かさない体とするかで自己同型群が変わってくるのです。
KのQ‐自己同型群(=ガロア群)は群の図の何に当たるのでしょう?
S:位数が6だからS3。つまりK/Qのガロア群は3次の対称群S3。
ではK/Lのガロア群(=Gal(K/L))に当たるのは何でしょう?
S:これは位数が3だから交代群A3だ。
では、L/Qのガロア群は?
S:そういえば何だろう?
S:Gal(L/Q)って、L(=Q(ω))とLの共役体(=Q(ω2))が作るQ−同型対応からなる群でしょう。
S:ωとω2を変える変える変換だから、前にやったτだ。(「中学生のもわかる」の9章)
S:この群の位数は2だから、それに対応するのは・・・
S:ここに書いてある剰余群S3/A3じゃないかな。
S:そうだよ。S3/A3={A3,τA3}でしょう。だから、A3L=L(A3によって変わらない部分体がL),τA3L=τLだ。
S:τLってLになるの?
S:Lのωとω2だけを変える変換だからちゃんとLになる。
S:だから、このガロア群はA3とτA3(=(23)A3)でできる剰余群と同じだ。
そうですね。実はこれがとても大事な対応で、L/Qのガロア群に対応する群はS3/A3(剰余群)です。
この観点でまとめると、
Gal(L/Q)=S3/A3
Gal(K/Q)=S3/{e}=S3
Gal(K/L)=A3/{e}=A3
S:L=Q(ω)={a0+a1ω:aiはQの要素}。
L(3√2)={a'0+a'13√2+a'23√4:a'iはLの要素}でしょう。
K/Lの自己同型群(ガロア群)ってどういう意味?
これは、A3={e,(123),(132)}(=×ω,×ω2)となります。
LはA3で不変な体だけど、拡張されたL(3√2)にはA3で変換される要素が含まれます。
だからA3がそのまま自己同型群になります。
S:τはωとω2を変えるだけだったけど、これはすべての体の元にωをかけるから3根は全て入れ替わりますね。
S:こうやって考えると、Gal(K/Q(3√2))もわかるね。
S:やっとわかったよ。自己同型群というのは体そのものの対称性を表しているんだ。
S:ところでQ(3√2)/Qのガロア群は考えられるの?
S:そもそもGal(Q(3√2)/Q)=S3/{e,(23)}は自己同型群にはならない。
ガロア群になるには共役体が一致し(正則拡大で)ないとダメなんだ。
S:そうか!群の方で言えば、剰余群になるためには割る方の部分群が正規部分群でないとダメ。
{e,(23)}は正規ではなかった。
S:体の方の正則拡大は群の方では正規部分群で表されているということか。正規部分群の方がわかりやすい。
S:とすると、正規部分群の正規部分群という様に正規部分群でつながっていないと解けないということですね。
S:まだあるよ。これらの剰余群は巡回群になっている。つまり可換群だ。
S:大事なことだ思うけど、さっきのガロア対応は結局矢印が対応しているんですね。
S:どういうこと?
S:矢印の対応は、矢印だけでなく「(分母)→(分子)」とセットで対応しているということです。
5,四次方程式のガロアの対応
これらのことを四次方程式で確かめてみよう。
というのは、前のサイトで四次方程式のガロア群と中間体を比べた時、
最後のクラインの群の位数が4なのに中間体の方は√、つまり二次になっていたのがとても気になっていた。
そこで、再度考え直してみながら、さっきのことを確かめてみよう。
S4(24元) Q
| 2 | Gal(L/Q)=S4/A4 2
A4(16元) Q(√)=L
| 3 | Gal(M/L)=A4/V4 3
V4(4元) L(3√)=M=Q(√,3√)
| 2 | Gal(N/M)=V4/{e,σ} 2
{e,σ} M(ω)=N=Q(√,3√,ω)
| 2 | Gal(K/N)={e,σ} 2
{e} N(√)=Q(√,3√,ω,√の組み合わせ24個)=K
左のガロア群は全て正規部分群で、体の次数と群の位数が対応している。
S:ガロア拡大と剰余群もちゃんと対応していますね。
S:こういう正規部分群の列があって、その間の剰余群は巡回群になっている。
これが可解群の定義になるのです。
S:正則拡大体をガロア群に置き換えて、群の方の性質で正則拡大を表したんですね。
S:そうすると、今までやってきたように体を拡大していけば(方程式の解き方でやれば)5次方程式の解の公式も求めることができるはずですね。
T:いよいよクライマックスですね。まず5次方程式のガロア群は?
S:5次方程式のガロア群は5次の対称群S5です。位数は5!=120。
S:その正規部分群(偶置換)は交代群A5で、位数は60。このA5が正規部分群を持っているのかどうか調べれば良いわけか。
今までの流れを図でまとめてみよう。
方程式の値 ――――――――――――― 根の置換
↓ ↓
(体) (群)
↓ ↓
方程式の値と根の関係 ―――――――― 根の置換が群をなす
↓ ↓
n√をとると方程式の値が変わる ――――― 置換群の部分群
↓ ↓
体の対称性が崩れる ―――――――― 置換が狭められる=部分群になる
↓ ↓
体の拡大 ――――――――――――― 部分群で置換されない体
↓ ↓
正則拡大だと自己同型群がある ―――― 剰余群(正規部分群によって生成される)
↓ ↓
方程式が解ける ―――――――――――― 可解群である
S:これも一つの回り道ですね。⇒【智慧とは回り道をするちから】
S:体の方の問題を群の方に置き換えて、より分かりやすい群で問題を解くわけだからね。
群の方の具体的な例を挙げておくよ。
【3・4次の対称群と交代群を求める(ジオジェブラ・ブック)】
【阿弥陀くじの数学(群論)(ジオジェブラ・ブック)】
目次へもどる