エッシャーのように そのⅢ
ひし形と正六角形によるしきつめ図形
オリガミでしきつめ図形を作ろう
初めてエッシャーの絵（しきつめ図形）を見た時、
いったいどうやって作ったのだろうと考えました。
そのときは全くわかりませんでしたが、
９２で正方形によるエッシャー図形の作り方がわかりました。
そして、他の絵も同じようにオリガミを切って作ることが
できることに気がつきました。
正多角形でしきつめることができるのは
正三角形・正四角形・正六角形の３つだけです。
まずは、このエッシャーの絵をよく見てください。
左のワニには正六角形が見えませんか。
よく見ると、
３匹のワニが一点で重なっているところがあります。
その３点を結んでみると、正三角形になります。
最初は正三角形かと思いましたが、
ワニとの面積が合いません。
エッシャーの下絵を見ると、
正六角形が書いてあります。
そして、さっきの正三角形の頂点は
この正六角形の頂点と重なっています。
もう一つの踊る人の絵にも六角形が見えますが、
下絵にはひし形が描いてあります。
とすると、正六角形とひし形を使って、
エッシャー図形を作ることができるはずです。
ひし形によるエッシャー図形
まず、ひし形を作ります。
正三角形を二つ張りつけた形です。
これを元に、有名なエッシャーの踊る人を作ってみましょう。
作り方は折り紙を切っていく正方形によるものと同じで、
切った所を別の場所に張っていく方法です。
辺は４つですから、正方形と基本的には同じです。
辺ａ'をはさみで切ってから、
Ｄを中心にして回転させ、隣のａに貼り付けます。
ａの足とｂはつないだまま、Ｂを中心にして回転させ、
ｂ'に貼り付けます。
下絵ができれば、
オリガミを重ねて切って、色別に貼り付ければ完成！
貼り付けると、切るところもわかります。
正方形の場合は一つの点に４つの図形が集まっていましたが、
ひし形の場合は３つ集まっています。
ａａ'→ａ'ａ→ａａ'と３本の線が来る事になり、
連続でつながることになります。
さてここで自分でエッシャー図形をつくらなければなりません。
ところがなかなかできないのです。
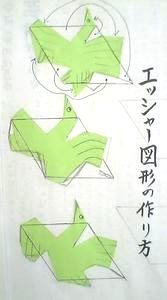方法はわかるけど意味のある図がなかなかできません。
苦慮すること４日間。
ついにできました。
踊る人の帽子を嘴にしてみたのです。
鳥ができそうでしょう。
そして、左の図のように変形していきました。
絵を創ることは数学の発見と同じです。
今回はオリガミではなく、
オリガミを貼り付けた厚紙を切り抜き、
それを元に紙にどんどんコピーしていきました。
これもなかなかきれいだし、
貼らなくても良いので、
簡単にできます。
さらに、スキャナーで取り込めば
色つけも簡単にできます。
正六角形によるエッシャー図形
次は、正六角形をオリガミで作ります。
左の図のようにａの面を切り取り、
ａ’の面に張ります。
張ったところから切り取った部分を
逆にａの所へ張ります。
同様にｂをｂ’に切り取り貼り付けます。
ｃをｃ’に切り取り貼り付けます。
修正は簡単にできます。
色別に貼り付けて完成。
もう六角形の痕跡は見ることができません。
目や背びれなどをつければ立派な絵になります。
ところでこの「ワニ」と「踊る人」は元の形が違うにも
かかわらず位置関係がよく似ています。なぜでしょう。
ひし形と正六角形の違い
ひし形の１つの図に入り込んでいる他の図は６つ。
正六角形の１つの図に入り込んでいる（接している）
他の図はやはり６つで同じ。
１つの点から３つの図がでてきているのも同じ。
図の構造は同じように見えます。
どちらも１つの絵に対して６つの絵が接しています。
図の向きで区別するとどちらも３種類です。
違いがないような感じがします。
比べるために元の形を並べてみましょう。
正六角形の場合は、並び方は一通りです。
向きの違いを色で表しています。
ひし形の場合は、並べ方のパターンは無限にあります。
ですが、この図形の場合は左のタイルのように並んでいます。
ひし形と正六角形は同じ
この二種類のタイルは、位置関係が同じようです。
三角形と六角形の双対的な関係からすると、
何か結びつきがあるような気がします。
正六角形を使って図を作る
六角形ということから連想して亀を作ることにしました。
図のように下絵を作ります。
切って張り合わせて、甲羅を描けば完成。
《拡大画像》
キツネ
コアラ
ゾウ
ペリカン
カメ
トリ
参考文献「エッシャーの宇宙」ブルーノ・エルンスト著・坂根巌夫訳・朝日新聞社出版
目次へもどる