傾億儘僯僂僗偺栤戣偼墱偑怺偄
擣幆偺乽偺傏傝偍傝乿偲徹柧偺偼偨傜偒
側偤偙偺尰徾偑偍偒傞偺偐乧尨棟偐傜愢柧偡傞乽偍傝傞乿
師偺恾偱丄C偺嬌慄傪堷偄偰偄傠偄傠嶌恾傪偟偰偄傞偲丄晄巚媍側尰徾偑尒偮偐偭偰偔傞丅
偡傞偲丄偦傟偼偳偆偄偆尨棟偐傜婲偙偭偰偔傞偺偐挷傋偨偔側傞丅
帋偟偵丄俹偺嬌慄忋偵堦揰傪抲偒丄偦偙偐傜墌偺嬌慄乮嵍偐傜係偮栚偺傾僀僐儞偺拞偵偁傞愙慄偺師乯傪嶌恾偟偰傒傛偆丅
偦偺揰傪摦偐偡偲嬌慄偼曄壔偡傞偗偳晄摦揰偑尒偮偐傞丅
偦傟偑俹偺嬌慄偺嬌丅
丂丂丂丂丂丂丂丂丂丂佱墌偺嬌偲嬌慄偺惈幙佲
偢偭偲埲慜亂乽嬌偲嬌慄乿擖栧 亃偐傜偙偺尰徾偑晄巚媍偩偭偨丅
偲偄偆偺偼丄偳傟偑尨棟側偺偐丄壗傪掕媊偲偡傟偽傛偄偺偐丄柪偭偰傢偐傜側偐偭偨偐傜偩丅
崱夞丄偄傠偄傠乽偝偐偺傏偭偰乮尨棟傪扵傞亖徹柧偡傞乯乿偄傞偆偪偵丄
乽儔丒僀乕儖偺掕棟乿偲偄偆偺偑嵟傕尨棟揑偱偼側偄偐偲姶偠偨丅
偦傟偱丄偙偙偐傜嬌慄傪掕媊偟偰丄崱搙偼乽偍傝乮愢柧偟乯乿偰傒傞丅
傕偟丄偦傟偱偡偭偒傝愢柧偱偒偨傜偙傟偑尨棟偲擣傔傞偙偲偑偱偒傞偼偢丅
偙傟偑亂儐乕僋儕僢僪偺曽朄亃側偺偩偲巚偆丅
偨偩偟丄尨榑偼乽偍傝傞乮愢柧乯乿偙偲偟偐弎傋偰偄側偄丅偦偙偵偼乽偺傏傞乿夁掱偑偁偭偨偼偢側偺偵丅
丂丂丂丂丂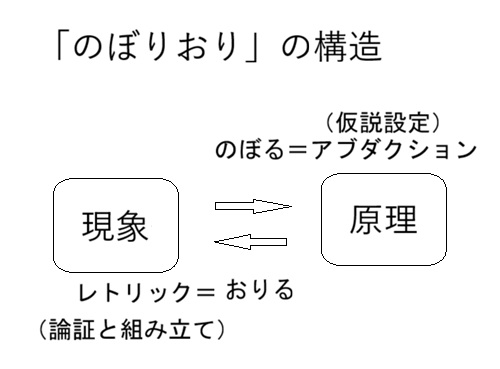
偙偺儗億乕僩偱偼丄偍傝傞乮愢柧乯偩偗偱側偔丄偺傏傞乮傾僽僟僋僔儑儞乯偙偲傕彂偄偰傒偨偄偲巚偆丅
傑偢丄嬌慄傪掕媊偟偰傒傞丅
壓恾偵偍偄偰丄乽俛偐傜墌俷傊偺愙慄偺愙揰傪寢傫偩慄乿偑嬌慄偱偁傞偑丄偙傟傪掕媊偵偡傞偲峴偒媗偭偰偟傑偆丅
偙偙偱偼丄俛偺嬌慄傪乽俛俷偲悅捈偱丄俷俤丒俷俛亖倰2偲側傞慄乿乮倰亖敿宎乯偲掕媊偡傞丅
偙偺掕媊偼丄憡帡側捈妏嶰妏宍偐傜捈偖偵摫偔偙偲偑偱偒傞丅
偦偟偰丄嬌慄偺惈幙偼慡偰捈妏嶰妏宍偺憡帡偐傜摫偒弌偝傟傞丅
帋偟偵丄乽儔丒僀乕儖偺掕棟乿傪徹柧偟偰傒傞丅
儔丒僀乕儖偺掕棟丂丂乽B偺嬌慄忋偺揰A偺嬌慄偼B傪捠傞乿
傑偢AO傊B偐傜悅慄BD傪堷偔丅偙偺BD偑A偺嬌慄偲側傞偙偲傪帵偡丅
僫價僎乕僔儑儞傪栠偟偰偐傜丄徹柧傪偨偳偭偰傒傛偆丅
丂丂丂丂丂丂丂佱乽儔丒僀乕儖偺掕棟乿偺徹柧佲
忋恾偺傛偆偵乽俠偺嬌慄忋偺揰俙偺嬌慄偼昁偢俛傪捠傞乿偙偲偑徹柧偱偒偨丅
偙偺掕媊偺椙偄強偼丄嶰妏宍偺憡帡偑巊偊傞偙偲丅
偙偺掕棟偐傜嬌偲嬌慄偵娭偡傞偄傠偄傠側惈幙偑惗傒弌偝傟傞丅
偱傕丄掕媊傪暿偺儌僲偵偡傞偲丄摪乆弰傝偵側偭偰偟傑偆丅
偩偐傜丄壗傪掕媊偲偟掕棟偲偡傞偺偐偱徹柧偑偱偒傞偐偱偒側偄偐偑暘偐傟傞丅
偮傑傝丄偝偐偺傏偭偨偙偲偑惓偟偄偐偼丄偍傝偰傒偰巒傔偰妋偐傔傜傟傞丅
掕棟偵偼偦偺媡偑偁傞丅媡偼忢偵惓偟偄偲偼尷傜側偄丅偱偼乽儔丒僀乕儖偺掕棟偺媡乿傪徹柧偟偰傒傛偆丅
乽俛偐傜墌偲岎傢傞捈慄傪堷偔丅偦偺岎揰偺愙慄偺岎揰偼俛偺嬌慄忋偵偁傞丅乿
乲徹柧乴俛偐傜墌偵捈慄俛俢傪堷偔丅偦偺慄偵懳偟偰俷偐傜悅慄傪堷偔丅
俀偮偺嶰妏宍偑憡帡側偺偱俷俤丒俷俛亖倰2偑尵偊傞丅
偦偺悅慄偲俛偺嬌慄偺岎揰偼俛俢偺嬌偲側傞丅
偮傑傝丄俙俢偲墌偺岎揰偺愙慄偼偙偺嬌偱岎傢傞丅
師偵丄慜偺恾偺乽俥俫偲俧俬偺岎揰偑俠偺嬌慄忋偵偁傞偙偲乿傪徹柧偟偰傒傛偆丅
傑偢丄壓恾偺傛偆偵弴偵嶌恾偟偰傒傞丅偙偺嶌恾偺弴斣偑戝愗側偺偱丄僫價僎乕僔儑儞傪栠偟偰偨偳偭偰傒傛偆丅
丂丂丂丂丂丂丂丂佱乽墌偵撪愙偡傞巐妏宍偺惈幙乿偺徹柧佲
屳偵嬌偲嬌慄偲側傞強偑億僀儞僩丅俠俙忋偺揰偺嬌慄偑俧傪捠傞偙偲傕捈偖偵傢偐傞丅
偦偟偰丄嬌偲嬌慄偺奣擮傪梡偄傞偲丄乽墌偵奜愙偡傞巐妏宍偺惈幙乿傕娙扨偵徹柧偱偒傞傛偆偵側傞丅
傾億儘僯僂僗偺栤戣
偲偙傠偱丄側偤偙偺嬌偲嬌慄傪扵偭偰傒傛偆偲峫偊偨偺偐偲偄偆偲丄
敪抂偼傾億儘僯僂僗偺栤戣丅
丂仺亂傾億儘僯僂僗偺栤戣偺嶌恾亃
乽暯柺偵偍偄偰梌偊傜傟偨3偮偺墌偵愙偡傞墌傪昤偗乿偲偄偆栤戣丅
偙傟偼憃嬋慄傗懭墌傪梡偄傞偲墌偺拞怱偑傢偐傝丄娙扨偵媮傑傞丅
偲偙傠偑丄暿偺夝偒曽乮僕僃儖僑儞僰偺曽朄乯偑偁傝丄偦傟偼嬌慄傗崻幉傪梡偄傞丅
偦偺曽朄偱幚嵺偵嶌恾偑偱偒傞偟丄GeoGebra偱摦偐偟偰傒傞偲妋偐偩偗偳丄
側偤偦偆側傞偺偐偼傢偐傜側偄丅
偪側傒偵乽嬌偲嬌慄乿偺奣擮偼丄偙偺僕儏僄儖僑儞僰偝傫偑尒弌偟偨偲偄偆丅
丂丂丂丂丂丂丂丂丂丂佱傾億儘僯僂僗偺栤戣佲
尨棟傪扵傞椃乽偺傏傝乿
偙偺恾傪嶌恾偟偰偄傞偆偪偵丄乽側偤偙偆側傞偺偩傠偆偐乿偲尨棟傪扵偭偰傒偨偔側偭偨丅
曽朄乮俫倧倵乯偑傢偐傞偲丄側偤乮倂倛倷乯偦偆側傞偺偐挷傋偨偔側傞偐傜偩丅
嶰墌偺愙慄傪嶌恾偟偰偄偰婥偑偮偄偨偺偑丄嶰墌偺愙慄偺俁偮偺岎揰偑堦捈慄忋偵暲傫偱偄傞偙偲丅
挷傋傞偲乽儌儞僕儏偺掕棟乿偲偄偆丅
丂丂丂丂丂丂丂丂佱儌儞僕儏偺掕棟佲
偙傟偼娙扨偵徹柧偱偒偦偆偩偑堄奜偲擄偟偄丅
壗偲偐捈娤揑偵徹柧偱偒側偄偩傠偆偐偲丄
偄傠偄傠挷傋偰偄偰丄嬻娫偱峫偊傞偲傢偐傝堈偄偲偄偆偙偲偑傢偐偭偨丅
仺乲徹柧乴亂儌儞僕儏乮暥庩乯偺掕棟偲榓嶼偺傢偐傝曽亃
偙偺俁杮偺愒慄偼俁墌偺嬌慄偲尒側偟偰傕椙偄丅
椺偊偽丄倅俹傪嬌慄偲偡傞偲丄拞怱偐傜倅俹傊偺悅慄偲倅偺嬌慄偺岎揰偑嬌偲側傞丅
偙傟偼屻偐傜廳梫側億僀儞僩偵側傞丅
偝偰丄俁墌偺恾佱傾億儘僯僂僗偺栤戣佲傪偄偔傜尒偰傕傢偐傜側偄丅偦偆偄偆帪偼偱偒傞偩偗扨弮偵偟偰傒傞丅
偮傑傝丄俁墌傪俀墌偵偟偰傒傞丅俁幰偺娭學傛傝傕俀幰偺娭學偺曽偑扨弮偵側傞偐傜丅
偦偆傗偭偰敪尒偟偨偺偑丄師偺恾偺戝偒偝偑堎側傞墌偱傕愙慄偺挿偝偑摍偟偔側傞偙偲丅
偮傑傝丄俤俻亖俥俿偱偁傞偙偲丅
偙傟偼娙扨偵徹柧偱偒偨丅乮偲偄偭偰傕3擔偐偐偭偨偗偳乯
丂丂丂丂丂丂丂佱乽擇偮偺墌偺愙慄偺惈幙乿偲徹柧佲
俀墌偵愙偡傞愙揰傪尒偮偗傞
偙偺忋恾偺嵟屻傪尒傞偲丄愙揰偺娫乮俻偲俿乯偺拞怱偑戝帠偱偼側偄偐丅
壓偺拞揰偲忋偺拞揰傪寢傫偩傕偺傪崻幉偲偄偆丅俛傪捠傞慄偑崻幉偱丄擇偮偺愙揰偺拞揰傪捠偭偰偄傞丅
崱搙偼崻幉偵偮偄偰挷傋偰傒傛偆丅
師偺儁乕僕仺亂崻幉偺惈幙亃
崻幉偼愙揰娫偺拞揰側偺偱丄戝彫俀墌偺愙揰傑偱偺嫍棧偑摍偟偄偙偲偑梊應偱偒傞丅
偙偺俀偮偺墌偺愙揰傑偱偺嫍棧偑摍偟偄偙偲偑丄傾億儘僯僂僗偺栤戣傪夝偔億僀儞僩偺條偩丅
偙偙偱婥偵側傞偺偑丄崻幉偑傢偐傟偽俀墌偵愙偡傞墌偑偳偆偟偰嶌恾偱偒傞偺偐偲偄偆偙偲丅
亂擇墌偺嬌慄偲崻怱偺娭學亃
偮傑傝丄愙揰傑偱偺嫍棧偑摍偟偄偲偄偆偙偲偼丄愙揰偼拞怱傪寢傇偲愙慄偲悅捈偵側傝丄
傕偆堦偮偺悅慄偲岎傢偭偨揰偼摍嫍棧偲側傝丄愙偡傞墌偑昤偗傞丅
師偺恾傪尒偰傒傛偆丅
俀偮偺愙揰偐傜岎揰俢偑尒偮偐傝丄俵倁亖俵俤側偺偱俢倁亖俢俤偲側傝丄俢偼愙墌偺拞怱偄偆偙偲偑傢偐傞丅
丂丂丂丂丂丂佱俀墌偵愙偡傞墌偺嶌恾佲
乮偪側傒偵丄憃嬋慄傾僀僐儞偱戝彫俀墌偺拞怱偲俢傪僋儕僢僋偡傞偲丄愙偡傞墌偺拞怱偺捠傝摴偑傢偐傞乯
偙偙偱婥偵側傞偺偑丄崻幉忋偺揰偐傜偳偆傗偭偨傜愙揰偑傢偐傞偺偐偲偄偆偙偲丅
偦傟偼丄偄傠偄傠妋偐傔偰傒傞偲尒偊偰偔傞丅
崻幉忋偺揰俵偐傜俀墌傊偺愙慄傪堷偔偲丄愙揰傑偱偺挿偝偑摍偟偔側傞丅
偮傑傝丄崻幉忋偺揰傪拞怱偵偟偨愙揰傑偱偺墌偑昤偔偙偲偑偱偒傞丅
偙偺墌偼忢偵偁傞掕揰傪捠傞丅忋恾偱偄偆偲俲偲L丅
媡偵尵偆偲丄俲傪捠傞墌傪昤偗偽愙揰偑傢偐傞偲偄偆偙偲偩丅
偦傟傪徹柧偟偰傒傛偆丅
壓恾乽崻幉偐傜擇偮偺墌傊偺愙慄偺挿偝偲嬌俧傊偺挿偝偑摍偟偄乿偙偲偺徹柧丅
偙傟偑徹柧偱偒傟偽丄崻幉偵偁傞拞怱偐傜俧傪捠傞墌傪昤偗偽愙揰偑帺摦揑偵媮傑傞丅
偙偺徹柧偵偼偐側傝帪娫偑偐偐偭偨丅乮堦偐寧傎偳乯
億僀儞僩偼傗偼傝嬌偲嬌慄偩偭偨丅偱傕丄偦傟偵婥偑偮偔偵偼偄傠偄傠側帋峴嶖岆偑偁偭偨丅
亂乽俀墌偺崻幉偺栤戣乿偑徹柧偱偒偨両亃
丂丂丂佱崻幉忋偺揰傪拞怱偲偡傞墌偑嬌俧傪捠傟偽丄墌偲偺岎揰偼愙揰偲側傞佲
偙偺傛偆偵徹柧傪彂偔偲娙扨偩偗偳丄偙偺徹柧偵帄傞傑偱偵偄傠偄傠帋峴嶖岆偟偰偄偨丅
嵟屻偵巚偄偮偄偨偺偑嬌偲嬌慄偩偭偨丅
偦偺帋峴乮巚峫乯偺夁掱丅偙偺僔乕僩偼僗僋儘乕儕儞僌偡傞偙偲偑偱偒傞丅
徹柧偲偼壗偐
偙偙偱丄徹柧偲偼壗偐傪峫偊偰傒傞丅
偄傠偄傠扵偭偰偄偔偲丄乽傕偟偐偟偨傜偙傟偑尵偊傞偺偱偼側偄偐乿偲偄偆尰徾乮壖愢乯偑尒偮偐傞丅
偱傕丄偦傟偼偁偔傑偱壖愢偱偁偭偰丄徹柧偝傟側偗傟偽妋幚偲偼尵偊側偄丅
徹柧偝傟偰偼偠傔偰掕棟偲側傝丄偦傟傪巊偆偙偲偑偱偒傞偺偩丅
偦偟偰丄徹柧偡傞偙偲帺懱偵傾僽僟僋僔儑儞乮壖愢愝掕乯偑昁梫偱偁傝丄偦偙偵傕乽偺傏傝偍傝乿偑偁傞丅
偦偺壖愢偺徹柧偼壢妛偺幚尡偲摨偠偱偁傝丄徹柧偝傟偨壖愢偼掕棟乮尨棟乯偲側傞丅
忋恾偺応崌偼丄俫偐傜偺嬌慄偑掕揰俧傪捠傞偙偲偵婥偑偮偄偨偙偲偑偒偭偐偗偩偭偨丅
亂怴偟偄掕棟偺徹柧偼幚尡偲摨偠亃
尨棟偐傜尰徾傪愢柧偡傞乮偔偩傝乯
尨棟傪尒偮偗偨傜丄師偼偦偺尨棟偐傜尰徾傪愢柧偡傞偙偲丅
偦傟偼丄儗僩儕僢僋傪梡偄側偗傟偽側傜側偄丅
儗僩儕僢僋偲偼丄愢柧偡傞弴斣乮傾僀僨傿傾乯寛傔丄偦傟傜傪榑棟揑偵愢柧偡傞偙偲丅
偮傑傝乽偍傝傞乿偙偲丅
亂徹柧偲傢偐傞僐僩亃
偙傟傑偱偺帠偐傜丄崻幉忋偺揰傪拞怱偲偟嬌俧傪捠傞墌偵傛偭偰愙揰傪尒偮偗傞偙偲偑偱偒偨丅
偝傜偵丄偙偺拞怱俶偲嬌俧偺娭學傪扵偭偰傒傞丅
栤戣偼俀墌偵愙偡傞墌偲偺愙揰傪尒偮偗傞偙偲偩偭偨丅
偙傟傑偱偺抦尒傪梡偄傞偲丄
乽崻幉傪巊偭偰丄愙慄傑偱偺嫍棧偑摍偟偄揰傪尒偮偗傞乿偙偲偑偱偒丄
偦傟傪梡偄偰俀墌偵愙偡傞墌傪嶌恾偡傞偙偲偑偱偒傞丅
棟桼偼丄慜偺佱俀墌偵愙偡傞墌偺嶌恾佲偺嵟屻偺恾偱丄俵傪摦偐偟偰傒傞偲丄
崻幉忋偺揰傪拞怱偲偡傞墌偺岎揰偼丄
拞怱偲寢傇偲擇摍曈嶰妏宍偑偱偒丄偦偺捀揰傪拞怱偲偡傞墌傪昤偔偙偲偑偱偒傞丅
俵偲俧偺嶌傞墌傪梡偄傞偲丄俀墌偵愙偡傞墌傪嶌恾偡傞偙偲偑偱偒傞偐傜丅
偱傕丄偙傟偩偗偱偼俁墌偵偼懳墳偱偒側偄丅崻幉偺拞怱揰偺埵抲偑掕傑傜側偄偺偩丅
偝傜偵挷傋偰傒傛偆丅壓恾偱丄摨偠墌偺愙揰偳偆偟乮倁偲倁1丆俤偲俢乯傪寢傫偱傒傞偲丄
偦偺岎揰偑崻幉忋偵偁傞偙偲偵婥偑偮偔乮惵偄慄偺岎揰乯丅
丂丂丂丂丂丂丂佱崻幉墌偺惈幙佲
偙傟偼媡乮崻幉偐傜偺慄偵傛偭偰愙揰偑傢偐傞乯傕尵偊傞偺偱偼側偄偐丅
偦偟偰丄偳偆偄偆慄偩偭偨傜惉傝棫偮偺偩傠偆偐丠丅
偦偙偱丄偙偺恾偺俵傪摦偐偟偰傒傞丅
偙偺寢傫偩慄偵晄摦揰偑偁傞偙偲偑傢偐傞丅
偙傟偼嬌偱偼側偄偐丠丅
偙偺嬌偺嬌慄偼壗偐丠
偦偙偱丄師偺恾偱傕偆彮偟怺傔偰傒傞丅
偙偺恾偱偼俠傪捠傞嬌慄俬俠傪愭偵堷偔丅偙偺嬌慄偺嬌偼倁偲俬俠偺嬌偩丅
嬌慄忋偺岎嵎偟偰偄傞揰傪嬌偲偡傞嬌慄偑丄俫俥傗俤俢偱偁傞偙偲偑傢偐傞丅
丂丂丂丂丂丂丂佱崻幉偲嬌偺娭學佲
師偺恾偺俼傗俽偺嬌慄偼丄俛傪捠傝丄俵偲俹偺愙慄偺岎揰傪捠傞丅
偙偺偙偲偼嬌偲嬌慄偺惈幙偐傜傢偐傞丅
俤傗俠傪摦偐偟偰傕岎揰俼丆俽偼昁偢俛偺嬌慄忋偵偁傞丅
堦尒晄巚媍偵姶偠傞偗偳丄嬌偲嬌慄偺娭學偐傜捈偖偵摫偔偙偲偑偱偒傞丅
壓恾偱俼偲俽偺嬌慄傪嶌恾偟偰傒傛偆丅
偦偟偰俵偲俥偺愙慄偑崻幉忋偱岎傢傞偙偲傪妋偐傔傛偆丅
偝傜偵丄俹偲俠偺愙慄偲偺娭學傕挷傋偰傒傛偆丅
丂丂丂丂丂丂丂丂丂丂丂佱俀墌偺嬌偲嬌慄偺娭學佲
偲偄偆偙偲偼丄
崱搙偼嬌慄偐傜俼偲俽傪媮傔丄俼偲俽偐傜崻幉忋偺揰傪尒偮偗傞偙偲偑偱偒傞偼偢丅
師偺恾偱妋偐傔偰傒傛偆丅
俢俥偲俤俶偼俠偺嬌慄丅俙偲俹偼倀倁偺嬌丅
俙偲俹偐傜崻怱偵捈慄傪堷偄偨帪丄偦傟偼倀偲倁偺嬌慄偲側傞丅
偙傟偑俁墌偺嬌慄偵摉偨傞丅
帋偟偵F傪摦偐偟偰傒傛偆丅
偙傟偼媡傪嶌恾偟偰傒傞偲椙偄丅
尨棟偼嬌偲嬌慄偺惈幙偐傜摫偗傞丅
壓恾偼嬌俥傪摦偐偟偰傒傞偲丄愙揰俫俬偺愙慄偺岎揰偑崻幉墌偲側傝丄愙偡傞墌傪嶌恾偡傞偙偲偑偱偒傞丅
丂丂丂丂丂丂佱擇墌偺崻幉偲嬌偲嬌慄偺娭學佲
偙傟偱俀墌傪俁墌偵奼挘偡傞偙偲偑偱偒傞丅
偲偙傠偱丄偙偺條側柺搢側偙偲偵側偤朞偒偢偵庢傝慻傔傞偺偐偲偄偆偲丄師偐傜師傊偲怴偟偄偙偲偑尒偮偐傞偐傜偩丅
偦偺尰徾傪側偤偩傠偆偐偲扵偭偰偄傞偲丄傑偨怴偟偄尰徾偑尒偮偐傞丅
偦傟偑壗偲傕尵偊偢妝偟偄丅椺偊偽丄俀偮偺墌偺戝偒偝偑堎側傞偺偱丄懳徧惈偑柍偄偺偩傠偆偲巚偭偰偄偨傜丄偪傖傫偲懳徧偵側偭偰偄傞偙偲偑抜乆傢偐偭偰偔傞丅
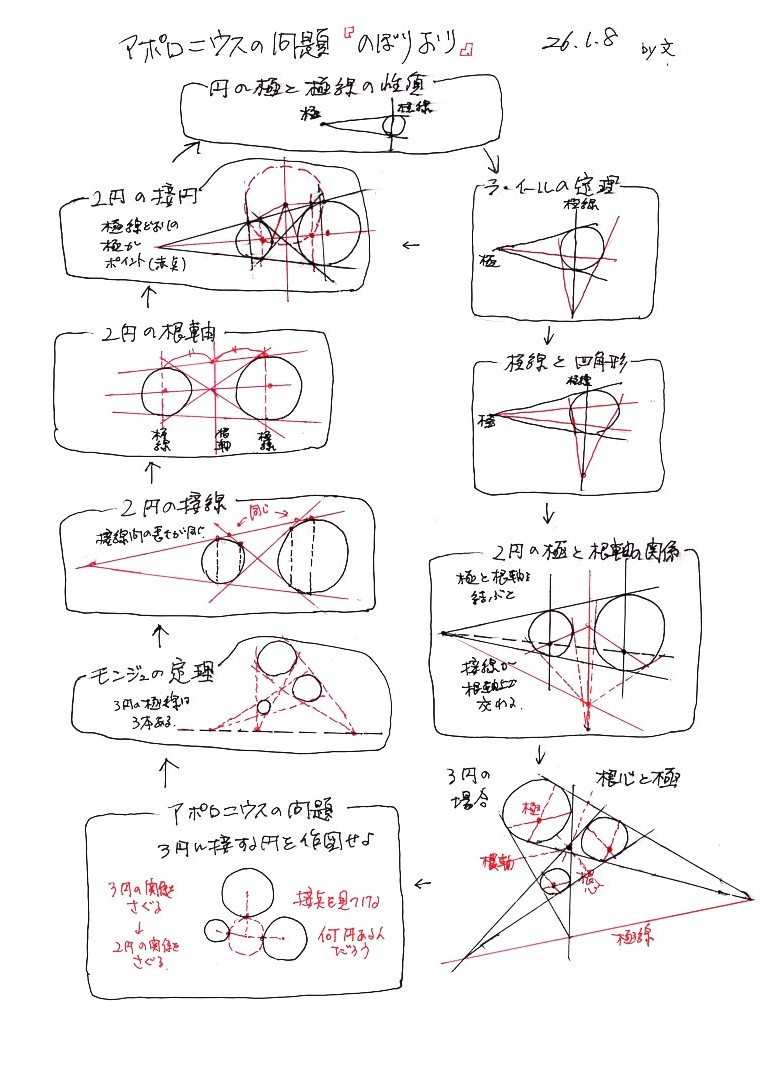
嬌傪捠傝崻幉偺堦揰偱岎傢傞捈慄偺墌偲偺岎揰偼愙慄偲側傞丅
師偺恾偱丄傑偲傔偰傒傛偆丅
崻幉偺偼偨傜偒偲嬌慄偺偼偨傜偒傪憤崌偡傞偲丄嬌慄偐傜俀墌偵愙偡傞墌傪嶌恾偡傞偙偲偑偱偒傞丅
巒傔偵嬌慄傪嶌恾偟偰偐傜丄嬌傪媮傔傞丅
偦偺擇偮偺嬌偑崻幉忋偺堦揰偲岎傢傞帪丄墌偲偺岎揰偺愙慄偺摦偒傪扵偭偰傒傛偆丅
僫價僎乕僔儑儞傪偨偳偭偰丄俙偲俼傪摦偐偟偰傒傛偆丅
丂丂丂丂丂佱俀墌偺崻幉偲嬌偲嬌慄偺娭學佲
偲偄偆傢偗偱丄嬌慄偲嬌偲偺娭學偐傜愙揰傪尒偮偗傞偙偲偑偱偒傞丅
俁墌偺応崌偺嶌恾偺巇曽偼丒丒丒丅壓恾偺僫價僎乕僔儑儞傪摦偐偡偲懱姶偱偒傞丅
丂丂丂丂丂丂丂佱俁墌偺応崌佲
奜懁偺愙揰偵愙偡傞墌傕嶌恾偟偰傒傛偆丅
俁墌偵愙偡傞墌偺嶌恾偺巇曽
嘆奺墌偺PW傪嬌慄偲偡傞嬌傪媮傔傞丅
丂乮媮傔曽丗奺墌偺拞怱偐傜PW傊偺悅慄偲PW忋偺揰偺嬌慄偲偺岎揰偑嬌慄PW偺奺墌偺嬌乯
嘇偙偺嬌慄PW偺奺墌偺嬌偲崻怱G傪寢傇丅
嘊偦偺慄偲墌偲偺岎揰偑俁偮偺墌偵愙偡傞墌偺愙揰偲側傞丅
嘋愙揰偲拞怱傪寢傫偩慄偺岎揰偑俁墌偵愙偡傞墌偺拞怱偲側傞丅
嘍側偍丄愙揰偼俇屄偱偒傞偑丄俁屄偢偮偺愙揰偱墌傪嶌恾偡傞丅
嬌慄PW忋偺椢揰偐傜奺墌傊偺嬌慄傪嶌恾偟丄崻怱G傪捠傞傛偆偵偡傞丅
偦偺帪丄嬌慄偲墌偺岎揰偑俁墌偵愙偡傞墌偺愙揰偲側傞丅
惓妋偵嶌恾偟傛偆偲偡傟偽丄俹倂傪嬌慄偲偡傞偦傟偧傟偺墌偺嬌偲崻怱偲寢傋偽傛偄丅
丂丂丂丂丂丂佱嶌恾偺曽朄佲
偙偺條偵丄俁偮偺崻幉偼侾揰偱岎傢傞丅偙傟傕徹柧偟側偄偲婥帩偪埆偄偗偳丄捈娤揑偵偦偆側傞偼偢偩偲妋怣偱偒傞丅
偮傑傝丄俀墌偺応崌偼崻幉偱岎傢傟偽椙偐偭偨偗偳丄俁墌偩偲偙偺崻怱偩偗偲側傞丅
偲偄偆傢偗偱丄師偺恾偑嵟廔僶乕僕儑儞丅
俁墌偵愙偡傞墌偼丄嬌慄偑係杮偁傝丄偦傟偧傟俀屄偺墌偑偱偒傞偺偱丄慡晹偱俉屄偁傞丅
拞怱偺埵抲傗敿宎傪偄傠偄傠曄偊偰傒傛偆丅
丂丂丂丂傾億儘僯僂僗偺栤戣偺姰惉宍
夝柧偡傞偺偵係儠寧丅彂偔偺偵堦偐寧偐偐偭偨偗偳妝偟偐偭偨丅
偙傟偼傑偝偵僱僈僥傿僽丒働僀僷價儕僥傿偺僩儗乕僯儞僌偩丅
傕偆堦偮婥偑偮偄偨偙偲偑偁傞丅
偦傟偼榑棟揑巚峫偵偮偄偰丅
徹柧偦偺傕偺偼榑棟偩偑丄偦偺徹柧偵帄傞巚峫夁掱偼乽榑棟乮巚峫乯乿夁掱偱偼側偄偲偄偆偙偲偩丅
乽徹柧偡傞摴嬝乿偲乽偦偺徹柧朄傪尒偮偗傞摴嬝乿偼堎側偭偰偄傞丅
偩偐傜丄徹柧傪嫵偊偰傕徹柧偱偒傞傛偆偵偼側傜側偄偺偩丅
偱傕丄帺暘偱偄傠偄傠傗偭偰傒偰徹柧偱偒側偐偭偨帪偵丄徹柧傪尒偨傜乽偦偆峫偊傞偺偐乿偲傢偐傞丅
偦偺偙偲偑徹柧朄傪尒偮偗傞傾僽僟僋僔儑儞偵偮側偑傞丅
GeoGebra偺僔乕僩亂傾億儘僯僂僗偺栤戣乮崻怱偲奜憡帡幉乯亃
丂丂丂丂丂栚師傊傕偳傞


