中３の数学のコツ

中３の数学は「長方形」と「正方形」で全てわかる！

３年生の各単元の流れとつながり　　

　すうがく通信　　　卒業記念特集号
数学を山にたとえると、今、君たちは、３年間の数学の学習を通して、中学校の数学の頂上に立っている。もちろんこれからも、山は続くだろうし、もっと高い山もあるだろう。しかし、ここで自分の登ってきた道をふり返ってみるのも意味があると思う。四月、君たちは「展開と因数分解」の山を登った。式の計算も、数の計算と同じ。まず、かけ算から。

１．展開と因数分解　→　４、数学アラビアンナイト
　　
←かけ算は，「面積図」で考えるとわかりやすい。
「展開」で使う法則は，分配法則。
分配法則とは，長方形の辺から面積を求めること。
つまり，「展開」とは，辺から長方形の面積を求めることである。
(χ＋３)(χ＋５)＝χ²＋(３＋５)χ＋(３×５)　→
(たて)×(よこ)＝(面積)

この逆が「因数分解」。
つまり，因数分解は，長方形の面積から辺の長さを求めることになる。
　χ²＋５χ＋６＝(χ＋２)(χ＋３)　→
(ばらばらの面積)＝(たて)×(よこ)

←　χ²＋２χ−８＝(χ−２)(χ＋４)

正方形の場合は平方公式。(χ＋３)²＝χ²＋６χ＋９


次にやったのが，平方根。

２．平方根　→　８、本の話

面積が４の正方形の一辺の長さを求めなさい。
面積が２の正方形の一辺の長さを求めなさい。

電卓で[２][×][＝]と押すとどうなるか。
電卓で[２][√]と押すとどうなるか。
面積が２の正方形の一辺の長さを√２とする。

√の足し算も面積図で考えることができる。
＋＝３　　→
Ａ.２つの辺を足した辺を１辺とする正方形の面積は？
　１８平方センチの１辺の長さは？
Ｂ.＝２だから合わせることができる。
　つまり，が３つある。だから３になる。


この平方根を使うと、こんな方程式も解くことができる。

３．２次方程式　→　４、数学アラビアンナイト

←　χ²＋６χ＝５を解こう。
　　
まず面積図で表す。
この長方形を正方形にしてみよう。
たりない所を加えよう。
正方形が完成した。
平方根を使って辺の長さを求めよう。
そうすると，χの値が求まる。
どうだい。これも正方形で解けるだろ。


さて、今までやってきた正方形の辺と面積の関係を，今度は関数で調べてみよう。

４．２次関数　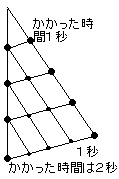→　６、ガリレオと落体の法則

１辺をχ�pとする正方形の面積を，ｙ平方センチメートルとする。
このｙの変化はどうなるだろうか。

面積の増え方は？…２乗の変化を調べる。

ｘ：0 1　2　3　4　5　
ｙ：0 1　4　9 16 25　　つまり、ｙ＝χ²　
これを二次関数という。

ここでは，今までやってきた正方形の辺の長さと面積の関係を関数としてとらえる。
二乗に比例する関係をグラフでは視覚で，表では対応としてとらえると，今までの学習とつながる。


次は、形の問題。

５．相似と比　→　 １６、米倉の定理　

方眼（正方形）を２倍に拡大する。
この三角形はどうなるか？
方眼を拡大しても形はおなじ。
これを相似という。
正方形を２倍に拡大すると面積はどうなるか。

長さは比例しても、面積や体積や重さが比例しないのはなんでだろう？それは二次関数だから。


さて，最後に今まで学んだことを活用する。

６．３平方の定理　→　３、ピタゴラスの世界

ピタゴラス数
　四角数＋四角数＝四角数
○○○　○○○○　○○○○●
○○○＋○○○○＝○○○○●
○○○　○○○○　○○○○●
　　　　○○○○　○○○○●
　　　　　　　　　●●●●●

正方形＋正方形＝正方形
直角三角形の各辺を１辺とする正方形を作る。そうすると、不思議な性質が見つかる。
右のパズルをやってみよう。
それがピタゴラスの定理の証明になっている。
この定理と平方根を使うと，直角三角形の辺の長さを求めることができる。数学で一番使われている定理だ。

以上，ざっと今まで学んできた数学をふりかえってみた。どうだろうか。少しは整理できただろうか。よけいこんがらかったって。心配するな。最近ではこういうことは，コンピュータが全てやってくれる。でも，コンピュータは時々，壊れる。コンピュータよりも，自分の感覚や思考を信頼しろよ。では、また。

もどる