![]()
1/3+(1/3)2+(1/3)3+・・・=1/2
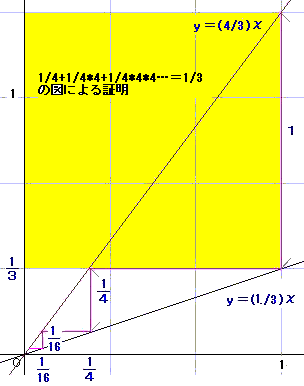
1/4+(1/4)2+(1/4)3+・・・=1/3
を図で説明してください。
1/n+(1/n)2+(1/n)3+・・・=1/(n−1)
の証明もお願いします。
![]()
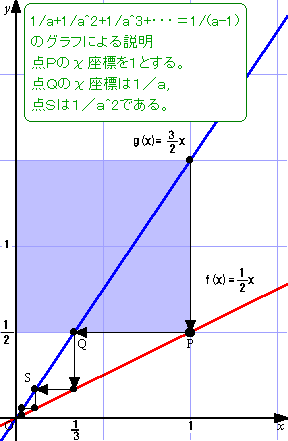
 グラフで説明すると
グラフで説明すると 課題を図で説明するとなると難しくて苦心しました。
概略を説明します。
f(x)=(1/(n-1))x…「赤」と
g(x)=(n/(n-1))x…「青」の
二つの正比例のグラフを描きます。
h(x)=g(x)−f(x)=x ですから、
この二つのグラフの間はxの値と同じになります。
例えば、x1=1/nとすると,
g(1/n)=1/(n-1)で
h(1/n)=1/n
f(1/n)=1/n(n-1)となります。
g(x2)=1/n(n-1)なので,
n/(n-1)・x2=1/n(n-1)
よって x2=1/n2
以下同様に, x3=1/n3
x4=1/n4
・・・となります。
これを、右のように二つのグラフの間に折れ線を描き込んで表わします。
x0=1から上へスタートして,f(1)で左に曲がり,g(x1)にぶつかったら,下に曲がり,f(x1)にぶつかったら,左に曲がって,g(x2)にぶつかったら,下に曲がるという様に無限の折れ線ができます。これはx=0で、y=0に収束します。
従って,図を見ると,
1/n+(1/n)2+(1/n)3+・・・=1/(n-1)ということがすぐわかります。(右の図)
具体的に、n=3で確かめてみてください。(下の図)
![]()
等比級数
ちなみに等比級数で証明すると,
1/n+(1/n)2+(1/n)3+・・・=Σとします。
両辺にnをかけると,
n・Σ=1+1/n+(1/n)2+(1/n)3+・・・
ですから
n・Σ−Σ=1 となり,
(n-1)・Σ=1
従って, Σ=1/(n-1)
となります。

1/2+(1/2)2+(1/2)3+・・・=1 は図で簡単に描けます。
線分1をとってその半分,残りの半分,残りの半分というようにやっていけば,
1に近づいていくことが直感的に見えます。
1/3+(1/3)2+(1/3)3+・・・=1/2 も簡単です。
上と同様にやれば,1/2に近づいていくことが見えます。
ところが,
1/4+(1/4)2+(1/4)3+・・・=1/3 は図では難しい。
それで,グラフで表わしてみたのです。