なぜ力の合成は平行四辺形になるの？
なぜ力の合成は平行四辺形になるの？
―天秤から平行四辺形へ、平行四辺形から天秤へ―
「なぜ力の合成は平行四辺形になるの？」
「力の平行四辺形」はベクトルのモデルであり、力の合成と分解はとても大事な法則だ。
でも、子どもたちに説明する時に、実験をやってから、誤差をごまかしながら、
「これは本当は平行四辺形になるんだよ。」と話していた。どこか釈然としない思いが残っていた。
「力の平行四辺形」はもっと根本的な原理から説明（証明）できるのではないかと感じていたからだ。
⇒【力の平行四辺形】ジオジェブラ
より根本的な原理は「天秤（てこ）の原理」だと、すぐに気がついた。
きっと天秤から説明できるはずと思っていたが、なかなかできずに時間だけが過ぎてしまった。それから１０年。
昨夜考えていたら、極めて自然に説明できる道筋が見つかった。
その道筋は、天秤の拡張である。
１、天秤の原理
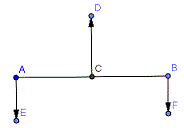天秤が吊り合っているのは、右と左の重さが等しいだけではだめで、支点Ｃまでの腕の長さも等しくなければならない。
もし、重さと腕の長さが異なっていたら、吊り合うためには、ＡＥ×ＡＣ＝ＢＦ×ＣＢとなることが必要となる。
下図の記号は異なっているが、この長方形の面積が等しい時に、天秤は吊り合っている。
これがアルキメデスの発見した「てこの原理」である。図からわかるように原理的には無限大の力になる。
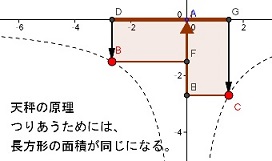（ジオジェブラのアプレット）天秤（てこ）の原理・・・てこは無限の力を生み出す
このつりあっている天秤は斜めにしてもは吊り合っている。
普通の天秤は重心が支点よりも下にあるので、ヤジロベエの原理で水平になるが、
この場合（支点＝重心）は斜めになってもは吊り合っている。
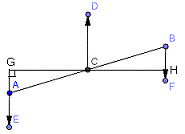
この時、右下図のように考えると、ＣＧ＜ＣＢであるが、先ほどの天秤の原理の腕の長さは、
左図のように腕と垂直にはたらく力と考えれば、天秤の原理は保たれている。
ＡＥ×ＣＧ＝ＢＦ×ＣＨ （力のモーメント）
実はここが一番大事なところで、これさえわかれば後は自然に導くことができる。
２、斜めの力でつりあうためには
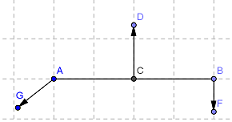Ａを斜めに引っ張って天秤をつりあわせたい。
Ｃは回転はできるが左右には動けないように固定されている。（上皿天秤またはＣを固定した剛体と考えよう！）
今までと同じ力で引けばＢが下がるはず。（力の大きさは線の長さで表す！）
では、吊り合うためにはどれだけの力χで引っぱればよいだろうか？
下の図のように、引っ張る角度をθとする。
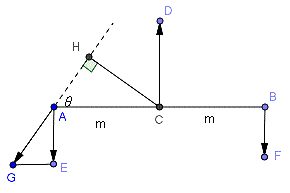天秤の原理を適用すると、ＡＧと垂直になるＣＨが腕の長さである。
ＣＡ＝ＣＢ＝ｍ，ＢＦ＝ＡＥ＝ａとする。
天秤の原理より、χ・ＣＨ＝ａ・ｍ
つまり、χ：ａ＝ｍ：ＣＨ
一方、△ＣＨＡは直角三角形で、∠ＡＣＨ＝∠ＧＡＥ（∠ＣＡＥ＝∠Ｒだから）
二辺の相似比とその間の角がそれぞれ等しいので、
△ＡＣＨ∽△ＧＡＥ
よって、∠Ｅ＝∠Ｈ＝∠Ｒ
これは、△ＡＥＧは直角三角形になることを示している。
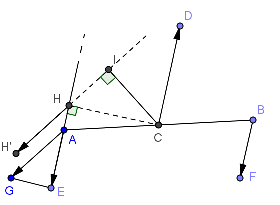
（脇道）
△ＡＥＧが直角三角形になることは、斜めになっても同様に成り立ち、∠Ｅは直角になる。
左図を見れば同じように成り立つことがわかる。
∠ＣＨＬ＝θ＝∠Ｇである。
なお、上の図で△ＡＥＧが直角三角形になるということは、χ（力ＡＧ）がＥＧとＡＥに分解されるということも示している。
つまり、力ＥＧとＡＥの合成は長方形の対角線＝χ（＝ＡＧ）となる。
３、両方の引っ張る向きを変える
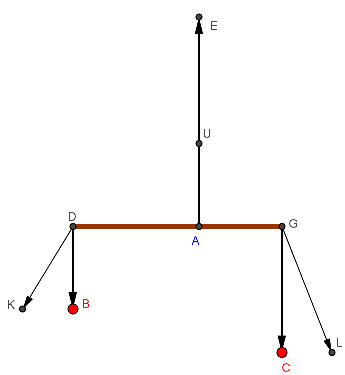― 天秤から平行四辺形へ ―
今度は、右図のように両方とも引っ張る向きを変えてみる。
支点はＡ（この支点は固定されておらず支点を上から吊るしていると考えよう）で、ＤとＧを異なる方向ＤＫにχの力、ＧＬにｙの力で引っ張る。
天秤がつりあう（水平になる）ためには、まず、横の力が同じでなければならない（作用反作用の原理）。
この力を便宜上１とする（ＢＫ＝ＣＬ＝１）。
また、天秤の原理から、ＤＢ・ＤＡ＝ＧＣ・ＡＧでなければならない。
この時、ＤＫを延長した線とＡＥが交わる点をＥ’、ＧＬを延長した線がＡＥと交わる点をＥ”とする。
実は、Ｅ’とＥ”は同一のＥであることを証明する。
なぜなら、ずれていると天秤がつりあわないからである。（ねじれてしまう）
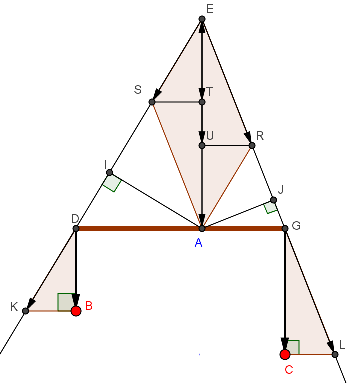《証明》
∠ＤＥ’Ａ＝θ，∠ＧＥ”Ａ＝γとする。
χとｙは２で考察したように、左図の直角三角形の斜辺になる。
ＥＡ⊥ＡＧとする。相似なので、
ＤＢ：１＝Ｅ’Ａ：ＤＡ ＧＣ：１＝Ｅ”Ａ：ＡＧ
Ｅ’Ａ＝ＤＢ・ＤＡ Ｅ”Ａ＝ＧＣ・ＡＧ
天秤の原理からＥ’Ａ＝Ｅ”Ａとなって、Ｅ’とＥ”は一致する。
つまり、Ｅ’＝Ｅ”＝Ｅである。
これは、天秤が吊り合っていて、ＢＫ＝ＣＬならば、延長線の交点は必ず垂線ＥＡ上にあるということを示している。
したがって、四角形ＥＳＰＲを考えることができ、（一般的にはＡとＰが一致しないがＡ＝Ｐと考えてもＯＫ）
四角形ＥＳＰＲは、△ＥＲＵ≡△ＰＳＴ、△ＥＳＴ≡△ＰＲＵとなり、平行四辺形となる。
ここで、天秤の合力ＤＢ＋ＧＣ＝ＥＰを考える。
天秤が吊り合うのは、支点を逆の方向に引っ張る力と等しいからである。
その力はＰＥであり、それの反作用がＥＰとなって、χとｙ二つの力の合力と等しくなる。
そして、この合力が平行四辺形の対角線となる。
よって、χとｙの合力は平行四辺形ＥＳＰＲの対角線と等くなり、天秤は平行四辺形となる。
つまり、χとｙの力の合成が平行四辺形の対角線になることが、天秤の原理から証明できたことになる。
（ジオジェブラのアプレット） 天秤から平行四辺形へ・・・天秤の原理から力の平行四辺形を導く
天秤から平行四辺形へ・・・横方向の力を自由に選ぶとき
４、力の平行四辺形から天秤の原理を導く
― 平行四辺形から天秤へ ―
ここまで考えてきて、ふと気がつくことがある。天秤の原理がより根本的原理なのかということである。
そこで、今度は逆を考えてみる。
力の合成が平行四辺形の対角線なら、（剛体の）天秤としてつりあっていることを示す。
上図で、点Ｅに力χと力ｙを加える。ＥＳとＥＲを延長する。合力は平行四辺形の対角線。
まず、どこに天秤棒と支点を作ったらいいのか。
(1)支点はＡにする。
(2)棒は平行四辺形の対角線に垂直にとる。
この天秤について、「二つの力が（天秤として）つりあっていること」を示す。
《証明》
平行四辺形なので、ＳＴ＝ＵＲ＝１とする。
ＤＫ＝χ、ＧＬ＝ｙとすると、
直角三角形が相似なので、
χ＋ｙ：ＡＤ＝ＤＢ：１ χ＋ｙ：ＡＧ＝ＧＣ：１
ＡＤ・ＤＢ＝χ＋ｙ ＡＧ・ＧＣ＝χ＋ｙ
∴ＡＤ・ＤＢ＝ＡＧ・ＧＣ
つまり、天秤の原理を導くことができた。
（ジオジェブラのアプレット）力の平行四辺形から天秤へ・・・力の平行四辺形から天秤の原理を導く
５、「てこの原理（天秤の原理）」と「力の平行四辺形」は同値である
まとめて図式化すると、
天秤 ⇔ 力の直角三角形 ←→ 力の平行四辺形
となる。
以上のことからことから、「天秤（てこ）の原理」＝「力の直角三角形」と「力の平行四辺形」が同値であることがわかる。
きっとアルキメデスは、自身の発見した「てこの原理」を使って、このように静力学を構成したのだろう。
自然の法則は、細部に宿っていることが実感できる。そして、ユークリッド幾何学が自然の現象を見事に表現していることに感動を禁じ得ない。
目次へもどる