「多チャンネル授業」による課題化
考える方法を身につけるために
１、「多チャンネル授業」
数学を「学ぶ力」とは、考える方法を身につけることです。考えることは「問い」を持つことです。
そして、その「問い」を生徒自身のモノにすることです。
そのために、私は次のような「多チャンネル授業」と名づけた授業プランに到達しました。
≪ねらい≫
(1) 一つの課題で、解決の方法がたくさんあるようにすること
(2) どの方法で取り組むのかを、生徒一人ひとりに選ばせること
(3) 遅れがちな生徒へ適切な援助をし、生徒同士の交流を促すこと
(4) 発表では、解き方の間のつながりを考え、教訓を導き出すこと
それは、次のような認識（わかるということ）のとらえ方が根底にあります。
○ 子どもによるやり方の選択（動機づけ・方向づけ・意味づけ）
○ 交流による認識の深化（自覚・編集・共有・一般化・理論化・実体化）
○ やり方の違いとその自覚（＝認識）による相対的理解
○ わかり方の自己選択による自分のわかり方の自覚
○ 環境世界の認識＝世界を変える＝自分が変わる
授業は、(1)課題提示と選択 (2)個人追求と交流 (3)発表と考察
という流れで行われます。もう少し詳しく言うと、
≪授業パターン≫
(1)、課題化（一人一人が発問によって何をしたらいいのかはっきりさせること）
５Ｗ１Ｈによる課題化・多チャンネル法による方法の提示・自分で方法を選ぶ
見通しをつける 方略の探究 発問を自分のものにすること 数学史から
単元によるアプローチの方法の違い 教具の意味と働き
教材→発問→具体的な課題→様々なやり方→やり方の選択
やり方 ⇒ 図を使う 式を使う 言葉を使う その他
(2)、取り組み（具体的な取り組み・聞きあい・板書・交流）
「丸つけ法」で自信を持たせる 個人的な取り組みから聞きあいへ
教えられ教えることによる思考のトレーニング
(3)、説明と質問と納得（自分のわかり方をつくりだす・自分の認識の自覚）
どういう順番で説明させるか プレゼンのトレーニング
なぜその質問をするのかという理由をつけて
「なぜそう考えることができたのか」
わかるとはどういうことかを教える
(4)、比較・ねうちなどによる意味の追及（それぞれのチャンネルをつなげる）
それぞれの理解・便利さ・応用の広さなどの発展を考える
(5)、まとめと次の課題（子どもが気がつかなかったことを示す）
意味をつかむ「ここに人類の歴史が埋まっている」
さらなる実在感と法則の追及
この様なスタイルをとるのは、
○ 帰納しか人間の思考は働かない。なぜなら人間の脳は解釈するだけだから。
○ 教師の発問は子どもの自問へ転化できるように考えぬかれてこそ、
数学のちからを、本当に子どものものにできるはず。
○ 動機づけは実在感が大きな根拠になる。
実体やモデル、例、それまでの体験をもとに、教具教材を工夫しイメージ化する。
という理由からです。
２、三平方の定理の「多チャンネル授業」プラン
次に具体的な授業プランを紹介します。
この授業は、一クラスを教師二人で行った授業で、板書と同時に、ＯＨＰとパソコンのタブレットを使って発表する方法をとりました。
提示の問題はワードで作成し、プリントして配ると同時に、パソコンでタブレットにも映します。
この授業は生徒たちの発表に重点がありますから、タブレットでの発表も試みました。
３、「多様な解き方を生み出す課題」を考えた単元指導計画
(1)【三平方の定理の発見その１ エジプトひも】
「エジプトひもを使って直角を作ろう」
という課題で、３：４：５の三角形を見つけます。
（「エジプトひも」は亀井喜久男さんの実践です）
(2)【三平方の定理の発見その２ ３：４：５の三角形】
「３：４：５の三角形は直角三角形か」
という課題を、方眼を用いて証明します。
具体的な数値を使った計算なので、説明することも簡単にできます。
(3)【三平方の定理の発見その３ 直角三角形ならば、a2＋ｂ2＝ｃ2になるか】
「３2＋４2＝５2が、他の直角三角形でも言えるのか」を調べます。
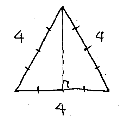
(4)【三平方の定理の証明】
「どんな直角三角形でもa2＋ｂ2＝ｃ2であることを証明しよう。」
これまでに、やったことを使って証明します。
(2)で具体的な数値でやっているので、比較的簡単にできます。
どの考え方を使うのかを、一人ひとりに決めさせます。
例えば、右図のような方法です。
(5)【三平方の定理を使って、直角三角形の辺の長さを求めよう】
「直角三角形ならば、2辺の長さがわかれば、他の１辺の長さがわかる」
ことを、正方形を描いて理解します。
平方根を使うことを忘れていますので、丁寧に説明します。
(6)【三平方の定理の逆】
「a2＋ｂ2＝ｃ2ならば、直角三角形である」ことを、パズルで証明します。
作り方は右の図のように切り、組み立てます。
この組み立てがパズルのようで案外難しいのです。
（それぞれの授業プリント）
このプランの特徴は、応用を含めながら原理を帰納的に探究していくというねらいを持っています。それは、生徒に考える方法を自らつかむことを志向するものとなっています。
原理を教えて、それを応用する演習という方向では意欲は生まれません。自分自身が発見できてこそ、応用しようという意欲が出てくるからです。
４、考える力を身につけるために
(1)自分のやれそうな方法を選ぶためには、自分の知識や学習方法を知っていなければなりません。
そして、どういう基準で選ぶのかも大切な「学ぶ力」となります。
自分自身の力を自覚することと、自分の目標を持つことがねらいです。
(2)自分で選んだ方法だからこそ、その方法に全力で取り組み、方向を見つけます。
その場合、易しいやり方と難しいやり方、式的なやり方と図的なやり方など多様なやり方を示し、
自分の力量を考えながら選ばせます。
(3)個別の指導の時に、できた子には別の方法に取り組ませ、
わからない子にはできている子の所へ相談に行かせます。
その方法を交流し、他の考え方と比べることで、自分自身の考えを深めることができます。
(4)発表は、観点を持って聞きます。
例えば「なぜ、はじめはうまく解けなかったのかを考えて」とか、
「自分のやり方とどう違うのか」「同じところはどこか」「どのやり方が一番自分に合っているか」
というように、自分とみんなの体験から何を引き出すかが大事であることを強調します。
(5)その教訓やまとめは、次の授業への足がかりとなります。
問題を解決した経験が、他の問題への挑戦意欲を促すからです。
５、実際の授業で
３のどの授業も面白かったのですが、ここでは(2)を取り上げます。
(2)の課題「３：４：５の三角形は直角三角形か」のねらいは、これを図で表して解くことによって証明の前段階にすることです。
しかも、３：４：５の三角形は最も応用が広く、便利です。
さらに、具体的な数値なので考えやすいのです。
課題１ 直角をはさむ３㎝と４㎝の三角形ＡＢＣを作ってみよう。
(1)ＡＢＣでＡＢの長さを求めるにはどうしたらいいだろうか。
(2)ＡＢ＝５㎝を示すことはできないだろうか。
(3)正方形を作ってみよう。（方眼を利用して）
(4)この正方形の面積はいくつか？（2５c㎡になるはず！）
(5)正方形の面積の求め方を考えよう。（5通りある！）
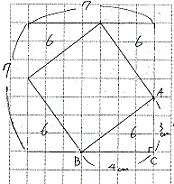
(1)～(4)は課題づくりの為の小さな発問なのでテンポよく進めます。
最後の(5)は黒板に5つの枠を書いて、どんな方法があるのか考えます。
Ａ,全体から余分なものをひく方法 Ｂ,正方形を分解する方法
Ｃ,１マスずつ数える方法 Ｄ,正方形を移動させる方法 Ｅ,その他
このうちのどの方法でやるのかを、挙手や名前カードを張って決定します。どうしても選べない子には、すぐにＴ２が個別に相談します。机間巡視では、やってあったら丸をつけ、「それを式にしてみて」「図をわかりやすくするといいよ」「黒板に書いてね」などと言います。
できていない生徒への援助は、どれを選んだのか、どこまで考えたのかを聞きながら丸をつけて、同じ方法でやっていた生徒の板書をヒントにし、時には「～君と相談して」と交流をさせます。誰も考えていないやり方を教える時もあります。
「発表に移ってもいいですか？」と確認し、全員が何らかの方法を考えたら発表します。
この時は、タブレットを使って発表しました。ノートと同じようにタブレットに向いてするので、書き込みながら、自分の考えた順に説明してくれました。質問もどんどん出ます。例えば、「どうしてそういうやり方を考え付いたのですか？」とか、「その式がわからない」とか言えるように要求します。
この発表のまとめは、「３：４：５の三角形は間違いなく直角三角形になる」でした。
そこで、最後の課題「３：４：５の間には、どんな関係があるだろうか？」は、全員で考えました。
９＋１６＝２５に気がつけばＯＫです。
みんなで考えてみるうちに、誰かが発見します。
みんな驚きます。
さらに、グランドにトラックを描くときに使えるということも気がつきます。
６、生徒はどんな時に意欲を見せるか
何をやればいいのかはっきりしているときに生徒たちは意欲を見せます。自分自身の力量を知りながら、その力で何ができるのかを考え、挑戦していきます。そして、他の人たちが考えたやり方と自分のやり方を比べながら自分自身の学習方法を見つめ直すのです。
目次へもどる