三角形の直角双曲線
― 三角形の垂心の意味 ―
1、刈屋点とフォイエルバッハ双曲線
S:三角形の「心」ってどうやって探すの?
T:一点で交わる3直線を探すんだ。一番簡単なのが三円交線を使う方法。三円交線は必ず一点で交わるからね。
例えば、ナポレオンが発見した点とか、フェルマーが使った点とかいろいろな「心」があります。
S:日本人の発見した「心」はあるの?
T:江戸時代の和算家安島直円の発見した「安島・マルハッチの点」というのがあります。
そして、ここで紹介したいのが刈屋他人次郎氏が1904年に発見した「刈屋点」。
S:どういう点なのかな?
まず、内接円と辺との接点を見つける。この接点と頂点を結んだ時にできる点がジェルゴンヌ点。
刈屋氏はこの3つの接点から垂線を立てて、その長さが同じになるようにしたら、やっぱり頂点と結んだ線が一点で交わることに気がついた。
S:スライダーを動かすと長さが変わり点が動くんですね。0の時はジェルゴンヌ点だ。
T:そうなんです。では、この刈屋点の軌跡は何を描くのでしょうか?
(スライダーをクリックしてカーソルで動かしてみよう)
S:双曲線だ。なぜ双曲線になるんだろう。これ三つの頂点を通っているよ。
S:それに垂心や内心も通っている。
T:なぜ双曲線になるのかはあとで詳しく調べることにして、次にキーペルト点を調べてみましょう。
2、キーペルト点とキーペルト双曲線
T:今度は長さではなく角度を同じにします。各辺の二等分線の角度を同じにするんだ。
その頂点とA,B,Cと結ぶと、一点に会する。
これを発見者の名前をとって、キーペルト点という。このキーペルト点の軌跡は?
S:やっぱり双曲線だ。垂心は同じだけど、今度は重心を通っている。
S:なぜ双曲線になるの?不思議だな。
T:刈屋点の軌跡をフォイエルバッハ双曲線といい、キーペルト点の軌跡をキーペルト双曲線といいます。
これらの双曲線は直角双曲線で相似です。
⇒【キーペルト点と刈屋点について】
S:直角双曲線って反比例のグラフですね。
T:そうです。この直角双曲線については面白い性質があります。
3、三角形双曲線
T:直角双曲線上に3点をとって三角形を描きます。この三角形の垂心はどこにあるのでしょうか?
S:垂心も必ず直角双曲線上にありますね。
三角形の頂点つまんで動かすと片方の双曲線に移る。面白いなぁ
S:では、頂点が楕円の上にあったら、垂心も楕円上にあるんですか?
T:このことについては、このブックを見てください。⇒【アポロニウス円錐曲線論】
ついでに、直角双曲線になるわけは次のブックで ⇒【相反共役点について】
三角形双曲線全般についてさらに知りたい人の為に⇒【三角形双曲線】
T:まとめると、三角形の頂点と垂心を通る双曲線は必ず直角双曲線になります。
そして、キーペルト双曲線は垂心Hと重心G、フォイエルバッハ双曲線は垂心Hと内心Iを通ります。
S:あれ?、今度は外心が仲間外れだよ。
T:そうですね。垂心と外心を通る双曲線があるはずだと思いますよね。
そこで、調べてみたんです・・・ちゃんとあるんですね。⇒【ジェラベク双曲線になる直線】
S:三角形には円や直線だけでなく、楕円や双曲線もあるんですね。
S:この双曲線は三角形の心も通っていますね。
さっきのオイラー線などの直線と双曲線とは何か関係があるのでしょうか?
T:そのことを探っていきましょう。
4、等角共役点と等距離共役点
○類似中線と類似重心
T:中線を結ぶと重心が現われます。
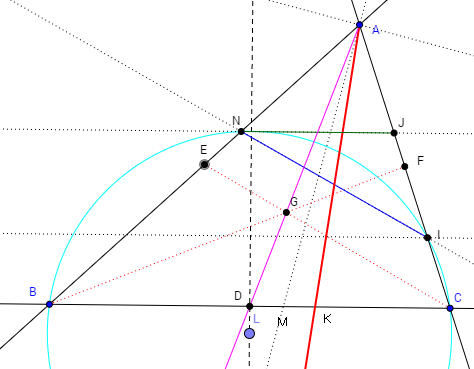
D,E,Fはそれぞれ中点、ADは中線です。中線なので、底辺と平行なNJは二等分に切断します。
中線の右の点線AMは∠Aの二等分線で、赤線AKと中線はこの二等分線で対称になっています。
つまり、∠DAB=∠CAKなのです。
S:さっきの垂心と外心の関係と同じだ。
T:そう、中線ADを角度に対して対称にしたAKを調べてみましょう。
AKはNJは等分していないけど、逆平行(逆の同位角が等しい直線)な線NIは二等分しているのです。
だからAKは類似中線と呼ばれます。
S:ということは類似中線を同様にして3本引けば類似重心が求まるということですね。
T:この重心と類似重心との関係を等角共役点と言います。
S:ということは、垂心と外心は等角共役点ということですね。
⇒【等角共役点についてさらに調べたい人のために】
○等距離共役点
T:今、角度に関して対称な線を引いたけど、中点からの距離を同じにする対称も考えることができます。
実は、どちらの線も一点で交わることが証明できます。これを等距離共役点と言います。
S:角に対して対称の場合が等角で、長さに対して対称の場合が等距離なんですね。
垂心と外心が等角共役点だったような点が等距離共役点でもないのですか?
T:もちろんあります。
有名な点では、ジェルゴンヌ点(内接円と辺との接点を結んだ点)とナゲル点(傍心円と辺との接点を結んだ点)は等距離共役点です。
⇒【等距離共役点についてさらに調べたい人の為に】
5、等角変形と等距変形
T:自由な点Pで、等角共役点P'を作図します。Pをつまんで動かしてみましょう。
等角共役点P'も同時に動きます。何か気がつきますか?
S:Pを真っ直ぐに動かすと、P'は曲線を描きますね。この作図はできますか?
T:いいアイディアですね。今度は直線上に点をとって、等角共役点を作図してみます。
S:その軌跡がどうなるのか見ればいいのですね。・・・
双曲線になりますね。今度は、直接双曲線を描かせることは出来ますか?
T:もちろんできます。5点を通る二次曲線を描けばいいのです。
○オイラー線の等角変形
T:まず、外心を通る直線を作ります。
外心を通るということは、双曲線はその等角共役点である垂心を必ず通ります。
S:直線を動かすことによって、直線と心のつながりがわかります。
T:これを等角変形といいます。
S:この双曲線は垂心Hを通っているので必ず直角双曲線になるのですね。
T:Eを動かして直線がオイラー線(垂心Hを通る)になるようにすると、ジェラベク双曲線になります。
S:Kは何ですか?
T:Kは重心Gの類似重心(重心の等角共役点)です。
これを通る直線は、重心を通るキーペルト双曲線になります。
S:ということは、内心Iと重ねると、内心を通るフォイエルバッハ双曲線になるんですね。
T:そうです。さらに同様のことを等距離共役点で考えると、等距変形が考えられます。
そして、そこから同様に3直角双曲線が生まれます。
S:2つの変形によって、3直線から3双曲線が生まれるのですね。
T:この2つの変形のそれぞれの3双曲線について、きれいな対称性が見つかります。
⇒【3直角双曲線の対称性について】
S:三角形の5心のつながりがわかりました。
そうすると三角形の他の心もこれらの直線と直角双曲線で分類できるような気がします。
T:この三角形の3直線と3直角双曲線とが描く図は、ともて美しいと感じます。
S:中点と垂足点→垂心と外心→キーペルト点と刈屋点→等角と等長(距離)
→等角共役点と等距離共役点→等角変形と等距変形→平行と逆平行・・・
などのように、対称的なものとつながりながら認識がどんどん深まっていく。
三角形って奥深いんですね。
目次へもどる
