 S丗奊傕悢妛偲娭學偑偁傞偺丠
S丗奊傕悢妛偲娭學偑偁傞偺丠俿丗乽儖僱僒儞僗乿偲偄偆尵梩傪暦偄偨偙偲側偄丅
S丗楌巎偱傗偭偨傛丅儗僆僫儖僪丒僟丒價儞僠乮侾係俆俀乣侾俆侾俋乯偲偐儈働儔儞僕僃儘乮侾係俈俆乣侾俆俇係乯偲偐桳柤側夋壠偑偄偨丅妋偐堄枴偼暥寍暅嫽偩偭偨偐側丅
俿丗儖僱僒儞僗偲偼丄14乣16悽婭偵僀僞儕傾偱揥奐偝傟偨丄巚憐丒寍弍丒妛栤側偳暥壔妶摦偺憤徧側傫偩丅
S丗俇侽侽擭慜偺僀僞儕傾偐丅擔杮偱偼幒挰帪戙偐丅
俿丗偦偺儖僱僒儞僗偺僟丒價儞僠払偺昤偄偨奊偲丄偦傟傑偱偺奊偑偳偆堘偆偺偐偑崱夞偺僥乕儅偱偡丅
奊偲悢妛丂乗墦嬤朄偼悽奅傪偳偆曄偊偨偺偐乗
 S丗奊傕悢妛偲娭學偑偁傞偺丠
S丗奊傕悢妛偲娭學偑偁傞偺丠
俿丗乽儖僱僒儞僗乿偲偄偆尵梩傪暦偄偨偙偲側偄丅
S丗楌巎偱傗偭偨傛丅儗僆僫儖僪丒僟丒價儞僠乮侾係俆俀乣侾俆侾俋乯偲偐儈働儔儞僕僃儘乮侾係俈俆乣侾俆俇係乯偲偐桳柤側夋壠偑偄偨丅妋偐堄枴偼暥寍暅嫽偩偭偨偐側丅
俿丗儖僱僒儞僗偲偼丄14乣16悽婭偵僀僞儕傾偱揥奐偝傟偨丄巚憐丒寍弍丒妛栤側偳暥壔妶摦偺憤徧側傫偩丅
S丗俇侽侽擭慜偺僀僞儕傾偐丅擔杮偱偼幒挰帪戙偐丅
俿丗偦偺儖僱僒儞僗偺僟丒價儞僠払偺昤偄偨奊偲丄偦傟傑偱偺奊偑偳偆堘偆偺偐偑崱夞偺僥乕儅偱偡丅
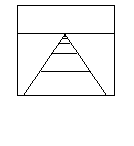
俿丗偙偺奊偼壗偵尒偊傞丠
S丗偳偙傑偱傕懕偔慄楬丅忋偺墶偺慄偼悈暯慄丅
俿丗偮傑傝偢偭偲峀偑傞抧暯偑昞傢偝傟偰偄傞傫偩偹丅偙偆偄偆恾傪摟帇恾朄偲偄偭偰丄儖僱僒儞僗偐傜巒傑偭偨昤偒曽偱偡丅
S丗墦嬤朄偼旤弍偱側傜偭偨傛丅傊乕丄儖僱僒儞僗傑偱偼側偐偭偨傫偱偡偐丅
S丗偠傖偁丄偦傟傑偱偼墦嬤偼偳偆傗偭偰昤偄偰偄偨偺偩傠偆丠
俿丗偦傟偼傑偨屻偱傗傞傛丅偲偙傠偱栤戣丅偙偺奊偺壓偺曽偼偳偆側偭偰偄傞丠
S丗偙偺慄楬偺懕偒傪昤偗偲偄偆偙偲丠
俿丗偦偆偱偡丅丂丒丒丒丒丒丒丒丒丒丒丂丂偐偗偨偐側丅偪傚偭偲愢柧偟偰傒偰丅
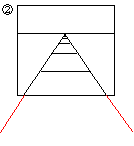
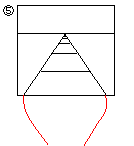
S丗(2)偼偍偐偟偄偲巚偄傑偡丅偙偺傑傑柍尷偵峀偑偭偰偄偔傫偱偡偐丅
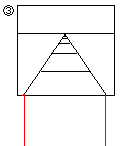
S丗慜偺奊傪偦偺傑傑昤偗偽偙偆側傞傛丅(3)偙偦偳偆偟偰暯峴偵側傞偺丠
S丗偩偭偰丄杮摉偺慄楬偼暯峴偩傠偆丅
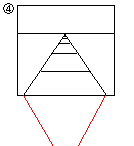
S丗(4)偼帺暘偺屻傠偺慄楬傪尒傞偲丄慜偲摨偠傛偆偵尒偊傞偼偢偩偐傜丅
S丗(4)偱媫偵愜傟傞偺偼偍偐偟偄偐傜丄(5)偺傛偆偵嬋偑偭偰尒偊傞偼偢偩偲巚偭偨丅
S丗側傫偩偐傒傫側偺堄尒傪暦偄偰偄偨傜丄傢偐傜側偔側偭偨丅偳傟偑惓夝側偺丠
俿丗偙傟傪峫偊傞偨傔偵偼丄摟帇恾朄偼偳偆傗偭偰昤偐傟偨偺偐傪抦傜側偔偰偼側傜側偄丅
S丗悈暯慄傪昤偄偰丄堦揰偐傜曻幩忬偵慄傪堷偗偽椙偄傫偠傖側偄丅
俿丗偦傟偼屻偐傜敪尒偝傟偨昤偒曽側傫偩丅摟帇恾朄偺尨棟偑敪尒偝傟偰偐傜丄娙扨側昤偒曽偑岺晇偝傟偨傫偩丅偩偭偰丄儖僱僒儞僗傑偱偼偙偆偄偆昤偒曽偼敪尒偝傟偰偄側偄傫偩偐傜丅偝偰丄偙偺摟帇恾朄偺尨棟偼偳偆傗偭偰敪尒偝傟偨偺偩傠偆偐峫偊偰傒傛偆丅
俿丗偦傟傪帵偡斉夋偑偁傞傫偱偡丅偙傟偼僪僀僣偺夋壠僨儏乕儔乕乮侾係俈侾乣侾俆俀俉乯偺斉夋偱偡丅
S丗昤偔傕偺傪傂傕偱寢傫偱昤偄偰偄傞丅
S丗榞偺拞偵巻偑偁偭偰揰傪偲偭偰偄傞丅
S丗偒偭偲丄尒偨偲偍傝偵昤偙偆偲偟偨傫偩側丅
S丗柺搢側偙偲傪偟偰偄偨傫偩側偀丅
俿丗摟帇恾朄偼傑偲傔傞偲丄擇偮偺憖嶌偵傛偭偰昤偐傟偰偄傞丅堦偮偼丄堦揰偐傜幚暔傪尒傞偙偲乮慄傪寢傇偙偲乯丅偙傟傪乽幩塭乿偲偄偆丅傕偆堦偮偼丄昤偔傕偺偲堦揰傪寢傫偩慄傪揰偲偟偰巻偵昤偔偙偲丅偙傟傪丄幩塭偟偨傕偺傪暯柺乮巻乯偱乽愗抐乿偡傞偲偄偆丅偮傑傝丄乽幩塭乿偲乽愗抐乿側傫偩丅偙偺偲偒愗抐偟偨暯柺偵昤偐傟傞偺偑摟帇恾側傫偩丅
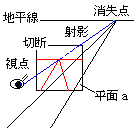 S丗偝偭偒偺暯峴側慄楬傪堦揰乮帇揰乯偐傜尒偰暯柺偺巻偵昤偔偲丄慄楬偼堦揰偵廤拞偟偰徚偊傞傫偩丅
S丗偝偭偒偺暯峴側慄楬傪堦揰乮帇揰乯偐傜尒偰暯柺偺巻偵昤偔偲丄慄楬偼堦揰偵廤拞偟偰徚偊傞傫偩丅
俿丗偙偺徚偊傞揰傪徚幐揰偲偄偄傑偡丅
S丗岦偙偆偵廤拞偟偰偄傞堦揰乮徚幐揰乯偺慜偵丄偙偪傜偵曅栚偱尒偰偄傞堦揰乮幩塭偺拞怱乯偑偁傞偲偄偆偙偲偱偡偹丅
S丗偦偆偐丅僨儏乕儔乕偺斉夋偺傛偆偵昤偔偺偑戝曄側偺偱丄堦揰乮徚幐揰乯偐傜曻幩忬偵慄傪堷偄偰昤偔傛偆偵側偭偨傫偩丅
俿丗偦偆偱偡丅儖僱僒儞僗偺夋壠偨偪偼丄堦揰乮徚幐揰乯偐傜昤偄偨屻偵偦偺揰偵寠傪偁偗偰丄棤偐傜嬀偵幨偟偰弌棃塮偊傪尒偨偦偆偱偡傛丅
S丗偦傟偑堦揰摟帇恾朄偺杮摉偺尒曽側傫偱偡偹丅
 俿丗偝偰丄偝偭偒偺栤戣傪偙偺尨棟偱峫偊偰傒傛偆丅栤戣偺億僀儞僩偼偳偆偄偆暯柺偱乽愗抐乿偡傞偺偐偲偄偆偙偲偩丅
俿丗偝偰丄偝偭偒偺栤戣傪偙偺尨棟偱峫偊偰傒傛偆丅栤戣偺億僀儞僩偼偳偆偄偆暯柺偱乽愗抐乿偡傞偺偐偲偄偆偙偲偩丅
S丗偦偆偐丅抧柺偵懳偟偰愗抐偡傞暯柺偑偳傫側妏搙偐偱堘偆丅
S丗暯柺偩偗偱側偔嬋柺偱愗抐偡傞偲偄偆偺偩偭偰峫偊傜傟傞傛丅
S丗(3)偼暯柺倎偑抧柺偵愙偡傞偲丄偦偺屻偵巻傪壓偵抲偄偰昤偗偽暯峴偵側傞丅
S丗(4)偼巻乮暯柺倎乯傪乢乛偙偆抲偗偽椙偄傫偩丅
S丗(2)偼戝偒側巻偱愗抐偟偨傕偺丅暯柺傪墑挿偡傟偽偄偄丅
S丗偁傟丠巹偨偪偼戝偒側侾枃偺巻偱愗抐偟偰偄傞偺偱側偔丄彫偝側巻傪墌摏偺傛偆偵偟偰偄側偄丠
俿丗椙偄帠偵婥偑偮偄偨偹丅巹偨偪偼乛丳乢偙偺傛偆偵巻傪栚偐傜摍嫍棧偵抲偄偰昤偄偰偄傞丅偱側偄偲抂偭偙偺曽偵昤偐傟偨傕偺偼戝偒偔側偭偰偟傑偆丅偙偺摍嫍棧偵偁傞巻傪偮側偄偱楢懕偝偣傟偽丄嬋柺偵側傝丄(5)偺傛偆偵嬋偑偭偰尒偊傞傫偩丅偦偺偙偲偵婥偑偮偄偨僄僢僔儍乕偼丄偙偺僗働僢僠傪昤偄偰偄傞丅
S丗僄僢僔儍乕偼嬋柺偱愗抐偟偨傫偱偡偹丅
俿丗僇儊儔偼栚傪儌僨儖偵偟偰嶌傜傟偨偗偳丄堘偆偺偼憸傪幨偡偲偙傠偑暯柺偲偄偆偙偲偩丅栚偼嬋柺偩偐傜幨偭偰偄傞憸偼堘偆丅
S丗偠傖丄U帤宆偵僼傿儖儉傪抲偄偨僇儊儔傪嶌偭偨傜丄偳偆幨傞傫偩傠偆丅僄僢僔儍乕偺奊偺傛偆偵幨傞偺偐側偀丅
亂僕僆僕僃僽儔偵傛傞俁揰摟帇恾朄偺昤偒曽亃
 亀僄僀儉僘偺晹壆亁
亀僄僀儉僘偺晹壆亁
S丗愭惗丄偦偺敔偼壗偱偡偐丠
俿丗偝偭偒儖僱僒儞僗偺夋壠偑丄徚幐揰偵寠傪偁偗偰尒偨偲偄偭偨偹丅偙偙偵擿偒寠偑偁傞偺偱丄尒偰偔偩偝偄丅
S丗恖偑擇恖偄偰丄塃偺恖偑偐側傝戝偒偄丅
俿丗忋偐傜擿偄偰傒偰丅僄僀儉僘偺晹壆偺摦夋
S丗偁傟丠恖宍偼摨偠戝偒偝偩丅
S丗偳偆偟偰丠
俿丗偙傟偼僄僀儉僘偲偄偆恖偑峫偊偨墦嬤朄傪棙梡偟偨嶖妎偺晹壆側傫偩丅乮晹壆偺嶌傝偼偄傃偮側偺偵丄擿偒寠偐傜尒傞偲惓曽宍偺晹壆偵尒偊傞丅乯
 偙傟偼丄偙偺擿偒寠偑徚幐揰側傫偩丅杮摉偼丄壓偺傛偆偵側偭偰偄傞傫偩偗傟偳丄忋偺條偵尒偊傞傫偩丅偒偭偲徚幐揰乮僉儕僗僩偺妟乯偐傜尒偨僟丒價儞僠偺乽嵟屻偺斢巂乿偼敆椡偑偁傞偲巚偆傛丅
偙傟偼丄偙偺擿偒寠偑徚幐揰側傫偩丅杮摉偼丄壓偺傛偆偵側偭偰偄傞傫偩偗傟偳丄忋偺條偵尒偊傞傫偩丅偒偭偲徚幐揰乮僉儕僗僩偺妟乯偐傜尒偨僟丒價儞僠偺乽嵟屻偺斢巂乿偼敆椡偑偁傞偲巚偆傛丅
S丗忋偐傜尒傞偲暯峴巐曈宍偺僞僀儖側偺偵丄擿偒寠偐傜尒傞偲惓曽宍偺僞僀儖偵尒偊傞丅偠傖偀丄偳傫側巐妏宍偱傕尒傞埵抲偵傛偭偰偼惓曽宍偵尒偊傞偺偐側丅
亂乽悽奅傑傞尒偊乿偺僙僢僩偺夋憸亃僥儗價僇儊儔偼偺偧偒寠偩両丠
俿丗偝偰丄偙偺摟帇恾朄偵傛偭偰丄儓乕儘僢僷偺恖偨偪偺奜奅傪尒傞栚偑曄傢偭偰偔傞丅偦傟偼丄奜奅傪嬻娫偲偟偰擣幆偟偩偟偨偙偲偩丅偦傟傑偱丄嬻娫偲偄偆奣擮偼偼偭偒傝偟偰偄側偐偭偨丅偙偺恾朄偵傛偭偰丄傕偺偑嬻娫偺拞偵埵抲晅偗傜傟傞傛偆偵側偭偨丅偮傑傝丄嬻娫傪乽擖傟暔乿偲峫偊傞傛偆偵側偭偨傫偩偹丅偦偟偰丄偦偺嬻娫偼柍尷偺峀偝傪帩偭偰偄傞偲峫偊傞傛偆偵側偭偨丅偐偔偰恖娫偼柍尷偺嬻娫乮塅拡乯傪庤偵擖傟偨丅
S丗偦傟偱壢妛偑敪揥偟偨傢偗偐丅
俿丗偲偙傠偑丄嬻娫傪嶌偭偨偲偄偆偙偲偼丄恖娫偼暔幙悽奅乮嬻娫乯偵暵偠崬傔傜傟偨偲傕偄偊傞傫偩丅傕偺偑嬻娫偺拞偵埵抲晅偗傜傟傞偲偄偆偙偲偼丄偦傟傪尒傞変乆偺帇揰傕嬻娫偺拞偵偁傞偲偄偆帠偩偐傜偹丅偦偟偰丄変乆偼嫄戝側乽擖傟暔乿亖乽嬻娫乿偺拞偵暵偠崬傔傜傟偰摦偄偰偄傞偩偗丅偱傕嬻娫偼乽擖傟暔乿偠傖側偄傛丅
S丗擖傟暔偠傖側偐偭偨傜丄壗側偺丠
俿丗惗妶嬻娫乮壠乯偲偄偭偨帪丄偦傟偼壗傕側偄乽擖傟暔乿側偺丠
S丗偄傠傫側儌僲傗僐僩偑偁傞丅偦傟偩偗偠傖側偄傛丅壠懓偑偄側偗傟偽惗妶嬻娫偠傖側偄丅
俿丗壠懓側傫偐偼娭學偩傠丅嬻娫偼娭學偲傕尵偊傞傫偩丅
S丗偦偆偄偊偽丄俼俹俧偺乽僎乕儉嬻娫乿偲偄偆偲悽奅抧恾偩偗偱側偔僗僩乕儕乕慡懱傕偝偟偰偄傞丅
S丗擔杮偱偼摟帇恾朄偵傛傞墦嬤朄偼敪尒偝傟側偐偭偨傫偱偡偐丠
俿丗擔杮偵摟帇恾朄傪揱偊偨偺偼僓價僄儖乮愰嫵巘払乯偲尵傢傟偰偄傞丅晜悽奊偵傕摟帇恾朄偱昤偐傟偨傕偺傕偁傞丅偱傕丄墦嬤朄偼摟帇恾朄偩偗偱偼側偔偰偄傠偄傠偁傞傫偩丅
俿丗擔杮乮搶梞乯偱偼墦偔偺傕偺偑戝偒偔側傞偲偄偆丄摟帇恾朄偺媡偺昤偒曽傑偱偁傞傫偩傛丅椺偊偽嫗搒攷暔娰偺亀朄慠忋恖奊揱亁傪尒偰偔偩偝偄丅
亂嫗搒崙棫攷暔娰亃儕儞僋丂丂亀媉墍嵳楃恾洜晽亁丂亀朄慠忋恖奊揱亁傪扵偟偰壓偝偄丅
S丗偳偆偟偰偙傫側昤偒曽傪偟偨傫偱偡偐丠
俿丗亀媉墍嵳亁偺奊偼丄嫗搒偺挰傪幬傔忋偐傜昤偄偰偄傞丅偙偺帪偵丄摟帇恾朄傪巊偆偲偳偆側傝傑偡偐丅
S丗墦偔偺曽傎偳彫偝偔側傝傑偡丅偱傕丄偙偺奊偺摴偼偢偭偲暯峴偵昤偄偰偁傞丅
俿丗偙偺奊偼墦偔偺曽傕慜偺曽偲摨偠傛偆偵昤偄偰偁傞丅偟偐傕丄晄帺慠偱偼側偄偱偟傚偆丅帪乆塤側傫偐傪巊偭偰徣棯傑偱偟偰偁傞丅偮傑傝丄帇揰傪堏摦偝偣偰偄傞傫偩丅僿儕僐僾僞乕偵忔偭偰僇儊儔傪摦偐偟側偑傜尒傞偺偲摨偠偙偲丅偙傟偔傜偄戝偒側奊偵側傞偲丄巹払偼僿儕偱偦傟偧傟偺強傊峴偭偰尒傞丅
S丗亀朄慠忋恖奊揱亁乮壓偺曽偺奊乯偺偙偺晹壆偼壗偩偐曄偩側偀丅
俿丗偙傟偼媡墦嬤朄偲偄傢傟丄墦偔偵峴偔偵偟偨偑偭偰峀偑偭偰偄傞傫偱偡丅
S丗偦偆尵偊偽丄庤慜偺恖傛傝傕墱偺恖偺曽偑戝偒偔昤偄偰偁傞丅
俿丗尒偰偄偰晄帺慠偵偼姶偠側偄偱偟傚偆丅偙傟偼丄墱偵偄傞恖偑廳梫側恖偺応崌偵巊偆庤朄偱偡丅嶌拞偺庡恖岞偐傜尒傞偲丄庤慜偺曽偺恖暔偼彫偝偔尒偊傞偐傜偱偡傛丅巹偨偪偑偙偺奊偺拞偵擖偭偰丄庡恖岞偵側傞傫偱偡丅
S丗傊乕丄偙傫側昤偒曽偼擔杮偩偗偱偡偐丅
俿丗偄傗丄拞悽偺儓乕儘僢僷傗拞崙丄挬慛偺奊偵傕摨偠傛偆側昤偒曽偑偟偰偁傞傕偺偑偁傞傛丅偮傑傝丄嬻娫偺偲傜偊曽偑堘偆傫偩側丅偲偙傠偑摟帇恾朄偑弌偰偒偰偐傜丄偙偆偄偭偨昤偒曽偼晄崌棟偱偁傞偲峫偊傜傟偨傫偠傖側偄偐側丅
 S丗慜偵暯峴側慄偼寛偟偰岎傢傜側偄偲偄偆偙偲傪廗偭偨傫偱偡偑丄偳偆偟偰暯峴側慄偑徚幐揰偱岎傢傞傫偱偡偐丅
S丗慜偵暯峴側慄偼寛偟偰岎傢傜側偄偲偄偆偙偲傪廗偭偨傫偱偡偑丄偳偆偟偰暯峴側慄偑徚幐揰偱岎傢傞傫偱偡偐丅
俿丗椙偄偲偙傠偵婥偑偮偒傑偟偨偹丅儖僱僒儞僗偺夋壠偨偪偼丄寶暔傪僨儏乕儔乕偺斉夋偺傛偆偵昤偄偰傒偰丄暯峴側慄偑嫹偔側傞偙偲偵婥偑偮偄偨丅偲偡傞偲偦偺慄傪墑挿偡傟偽昁偢岎傢傞偼偢丅偦偙偐傜徚幐揰偑敪尒偝傟偨傫偠傖側偄偐側丅
S丗昤偄偰傒偰傢偐偭偨傢偗偐丅
俿丗僼儔儞僗偺寶抸壠僨僓儖僌乮侾俆俋俁乣侾俇俇俀乯偼崱孨偑峫偊偨傛偆偵丄愗抐偝傟偨暯柺偱偼暯峴慄傕徚幐揰偱岎傢傞偲偙傠偑婥偵側偭偨丅偦偟偰丄幩塭偱愗抐偝傟偨嬻娫乮暯柺乯偱偼暯峴偵尒偊偰偄偰傕丄偦傟傪幩塭偡傟偽岎傢偭偰偄傞偲峫偊偰傕椙偄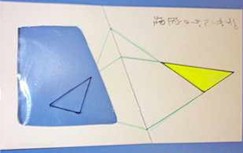 偺偱偼偲傂傜傔偄偨丅
偺偱偼偲傂傜傔偄偨丅
丂偝傜偵尰幚偺嬻娫偱傕丄暯峴慄偼岎傢偭偰偄傞偲峫偊偨曽偑崌棟揑偱偁傞偲峫偊丄偦偺岎傢傞揰傪乽柍尷墦揰乿偲柤晅偗偨丅偦偟偰丄摟帇恾朄傪徻偟偔尋媶偟偰怴偟偄婔壗妛傪憂傝弌偟偨丅偦傟傪乽幩塭婔壗妛乿偲尵偆丅
丂偝偭偒丄巐妏宍偑惓曽宍偵尒偊傞偲偄偆榖偑弌偨偹丅幩塭偝傟傞偲捈慄偼捈慄偵側傞偗偳丄宍傗戝偒偝偼曄傢傞傫偩丅椺偊偽丄墌偼懭墌偵側傞傛丅偦偆傗偭偰幩塭丒愗抐偟偰傕曄傢傜側偄傕偺偼壗偐傪尋媶偡傞婔壗妛偑偱偒傞偺偱偼丄偲峫偊偨偺偩丅
S丗偦傟偼栶偵棫偮偺丠
亂僕僆僕僃僽儔偵傛傞僨僓儖僌偺掕棟偺僔儏儈儗乕僔儑儞亃
俿丗嵟嬤偼僷僜僐儞偺僎乕儉傗僔儈儏儗乕僔儑儞偺攚宨偵巊傢傟偰偄傞丅
S丗僎乕儉偺夋柺偵墱峴偒傪偮偗傞偨傔偵丄幩塭婔壗妛乮摟帇恾朄乯傪巊偭偰偄傞偺偐丅
俿丗偙偙偱丄斵偑敪尒偟偨乽僨僓儖僌偺掕棟乿傪徯夘偟傛偆丅嵍偺擇枃偺幨恀傪尒偰偔偩偝偄丅偁傞帪丄僨僓儖僌偼摟帇恾朄傪巊偭偰嶰妏宍偑偳偆曄壔偡傞偺偐挷傋偰偄偨丅乮忋乯傑偢曅栚偱墿怓偄嶰妏宍傪尒側偑傜丄摟柧側僔乕僩偵廳側傞傛偆偵昤偄偨丅偦偟偰丄偦傟傪峀偘偰傒傞偲丄乮壓乯懳墳偡傞嶰妏宍偺曈偺墑挿慄偼擇偮偺暯柺偺岎傢傞強乮慄乯偱岎傢傞丅偮傑傝丄嶰偮偺岎揰偑堦捈慄忋偵偁傞偲偄偆偙偲偵婥偑偮偄偨偺偩丅
S丗偙傟偼丄堦斣嵟弶偵傗偭偨慄楬偺壓傪昤偄偨帪偺嘊傗嘋偲摨偠偩傛丅幚嵺偺慄楬偲奊乮愗抐暯柺乯偺慄楬偼昁偢岎傢傞丅傑偨丄暯柺偲暯柺偺岎傢傝偼昁偢堦捈慄偵側傞偐傜丄懳墳偡傞嶰妏宍偺曈偺墑挿慄偺岎揰偼堦捈慄忋偵偔傞丅嘊傗嘋偼奊偺掙偺慄偑擇偮偺暯柺偺岎慄側傫偩丅
俿丗偦傟偑偙偺掕棟偺徹柧偱偡傛丅
S丗偲偙傠偱暯柺偵昤偄偨偺偵丄棫懱揑偵尒偊傞偺偼偳偆偟偰偱偡偐丠
S丗椉栚偱尒偰偄傞偐傜偠傖側偄丠
俿丗偙傟傪曅栚偱尒側偑傜傊偙傫偩恀傫拞偺妏傪晜偐傃忋偑傜偣傞傛偆偵偟偰傒偰丅
S丗偁偭両棫曽懱偵尒偊傞丅摦偐偡偲婥帩偪埆偄丅
俿丗偙傟偼嶰偮偺暯峴巐曈宍偐傜偱偒偰偄傞丅嶰偮偺暯峴巐曈宍偼丄曅栚偱尒偰傕棫懱偵尒偊傞丅
S丗儃僋偼椉栚偱傕棫曽懱偵尒偊傞傛丅乮偙傟傪幚嵺偵嶌偭偰傒偰壓偝偄丅乯
俿丗偙偺傛偆偵摟帇恾朄傪巊傢側偔偭偰傕丄墱峴偒偼姶偠傞帠偑弌棃傞傫偱偡傛丅偳偆傗傜巹偨偪偺帇妎乮姶妎乯偼棫懱揑偵尒偊傞乮擣幆偡傞乯傛偆偵偱偒偰偄傞傜偟偄丅偮傑傝丄栚偱棫懱偵尒傞偺偱偼側偔丄摢偱尒偰偄傞傫偩傛丅擼偼棫懱揑偵弌棃偰偄傞傛偆偩丅傕偭偲傕丄偙傟傕孭楙偟偰恎偵偮偗傞傕偺偺傛偆偩偗傟偳丅
亂棫懱帇偺偄傠偄傠亃亀棫懱幨恀娰亁傊偺儕儞僋
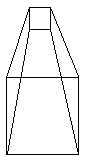
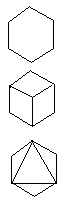 俿丗嵍偺恾偼壗偑尒偊傞丅
俿丗嵍偺恾偼壗偑尒偊傞丅
S丗偙傟偼挼傃敔偲楲壓偑尒偊傑偡丅
S丗慄偑壗杮偐堷偄偰偁傞偩偗側偺偵丄偳偆偟偰擇庬椶偺棫懱偵尒偊傞傫偩傠偆丅
乮懢梲岝慄丄俷俫俹偱塭傪嶌偭偰尒偣傞丅乯
俿丗偙偺榋妏宍偼偁傞棫懱偺塭偱偡丅偙偺棫懱偼壗偩傠偆丠
S丗棫曽懱丅乮榋妏宍偵慄傪擖傟傞偲棫曽懱偵尒偊傞丅乯
俿丗偱偼丄偙傟偼丠
S丗棫曽懱丅摨偠偱偡丅
俿丗杮摉偵偦偆偐側丅乮摦偐偟偰傒傞丅乯
S丗偁傟丄偪偑偆丅偱傕側傫偩傠偆丅
俿丗偙傟偱偡丅乮尒偣傞丅乯
S丗惓敧柺懱偩丅
俿丗惓榋妏宍偵慄傪嶰杮壛偊傞偩偗偱丄棫懱偵側傞傫偱偡偹丅偙傟傕摢偺拞偱棫懱傪嶌傝忋偘偰偄傞偲尵偭偰偄偄偲巚偆丅偙偺偙偲偼儖僱僒儞僗傛傝偼傞偐慜偺恖偨偪傕抦偭偰偄偨丅
俿丗孨偨偪偼嬻娫偲偄偆偲偳傫側僀儊乕僕傪帩偭偰偄傞丠
S丗棫曽懱丅晹壆丅擖傟暔丅僩儞僱儖丅媴丅
俿丗棫曽懱偲媴偺僀儊乕僕偼偪傚偭偲堘偄傑偡偹丅偳偪傜傕峀偑偭偰偄傞僀儊乕僕偑偁傞偗偳丅棫曽懱偼慜屻嵍塃忋壓偵峀偑傞丅
 俿丗師偺奊偱丄慜偼塃偐嵍偐偳偪傜偱偡偐丠
俿丗師偺奊偱丄慜偼塃偐嵍偐偳偪傜偱偡偐丠
S丗(1)偼嵍偱偡丅
S丗(2)偼塃偱偡丅婘偺慜偵棫偪側偝偄偲尵傢傟偨傜丄塃偩傛偹丅
S丗(3)偼嵍偱偡丅
S丗(4)偼嵍偱偡丅偩偭偰枹棃偵岦偐偭偰偄傞偐傜丅
俿丗(4)偼杮摉偐側丅俛丏俠偭偰抦偭偰傞丅俛倕倖倧倰倕丂俠倛倰倝倱倲乮婭尦慜乯偲偄偆傛丅倐倕倖倧倰倕偼栿偡偲埲慜偩傠丅僉儕僗僩傛傝傕愄側傫偩丅偲偙傠偱丄倎倖倲倕倰偼屻丅倐倕倖倧倰倕偼丠
S丗倐倕倖倧倰倕偼慜丅偁傟丠偳偆偟偰丅
俿丗尰嵼偺抧揰偵棫偭偰丄夁嫀偺曽傪岦偄偰偄傞偲峫偊偰傕椙偄偩傠偆丅夁嫀偼屻偵偁傞傫偠傖側偄丅夁嫀乮楌巎乯偼慜偵偁傞傫偩丅擔杮岅偱傕慜悽偲偄偭偰夁嫀偺偙偲傪慜偲巊偆応崌傕偁傞傛丅
S丗(3)偱偼彂偄偰偄偔曽偑慜偩偐傜丄乽傕乿偺曽偑慜偲傕偄偊傞傛丅
俿丗幚嵺偵僶儞僣乕岅偱偼乽傕乿偺曽傪慜偲尵偆偦偆偩丅婘偩偭偰帺暘偵岦偄偨曽傪慜偲尵偭偰傕偄偄丅
丂偙偺傛偆偵乽慜屻苽瀭蓙A壗傪婎弨偵偟偰偄傞偺偐偲峫偊偰傒傞偲丄帺暘偺乽恎懱乿傪尦偵偟偰偄傞丅偲偡傞偲丄嬻娫偼乽恎懱乿偐傜弌偰偒偨偲偄偊傞丅巹偨偪帺恎偺乽恎懱乿偑嵟弶偺嬻娫偱丄偦偺乽恎懱乿偑偳傫偳傫峀偑偭偨傕偺偑乽悽奅乮尰幚嬻娫乯乿側傫偩丅偩偗偳丄巹偨偪偼嬻娫偲恎懱偲偼暿暔偩偲峫偊偰偟傑偭偰偄傞傫偠傖側偄偐側丅傕偆堦搙丄嬻娫傪帺暘帺恎偺乽恎懱乿偐傜偲傜偊捈偟偰傒傛偆傛丅
丂椺偊偽丄幚尡偲偼帺慠傪乽恎懱乿偱峫偊偨傝乽恎懱乿偱尒傞偙偲偱偁偭偰丄摎偊傪妋擣偡傞偙偲偱偼側偄傛丅傠偆偦偔偺壢妛偱桳柤側僀僊儕僗偺暔棟妛幰僼傽儔僨傿乕偼丄懠偺恖偑幚尡偟偨寢壥偵偮偄偰偺堄尒傪媮傔傜傟傞偲丄偦偺幚尡傪帺暘偑傗偭偨偙偲偑側偄偲傎偲傫偳棟夝偱偒側偄偺偱丄帺暘偱幚尡傪傗偭偰偐傜僐儊儞僩偟偨偲尵傢傟偰偄傞傛丅
丂懯栚墴偟偱傕偆堦偮丅乽恎偲怱偼暘偐偮偙偲偑偱偒側偄丅偩偐傜丄怱偺側偄恎偼暔傪姶偢傞偙偲偑偱偒偢丆恎偺側偄怱偼棟傪抦傞偙偲偑偱偒側偄丅鄮q戝塰乮扸堎彺丄娾攇暥屔)
嶲峫暥專
亀捑栙偺僐僗儌儘僕乕亁扥塇晀梇丆梀惎幮丅亀奊夋嬻娫偺揘妛亁嵅摗峃朚丆嶰尦幮丅
亀嬻娫偵偮偄偰偺悢妛亁僋儔僀儞丆搶嫗恾彂丅亀僄僢僔儍乕偺塅拡亁B丏僄儖儞僗僩丆挬擔怴暦幮丅亀恎偺峔憿亁巗愳峗丅