ニューラルネットワークを探る
Rのnnetを使ってNNを調べる
1、ニューラルネットワーク
「AI」についていろいろ調べると、「ニューラルネットワーク」が重要であることがわかった。
その原理は「バックプロパゲーション」といい、微分を使うということが書いてあった。
これについては、統計処理で「回帰直線の求め方」を調べた時、微分を使って求めるというのをやったので大体はわかる。
改めて統計と行列が大事だと思った。
ここまではよかったけど、「デープラーニング」の所で仕組みがわからなくなってきた。
でも、「ニューラルネットワーク」が最初の足掛かりだとわかったので、これを徹底的に調べてみようと思う。
と言っても、実際にやってみることがわかる一番の近道だ。
これから「ニューラルネットワーク」をNNと略す。
NNは脳細胞のモデル化であり、脳の構造を数学的に表している。
脳細胞はネットワークである。ネットワークというと、二つのNNが考えられる。
1つは階層型NN (これがNNのモデル)
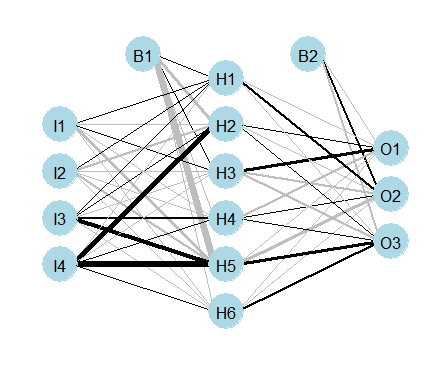
もう一つは相互結合型NN (これは私たちの脳の「意味ネットワーク」)
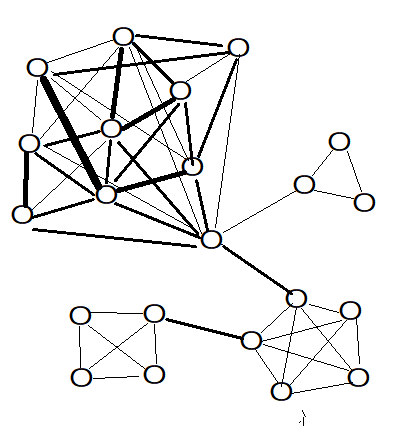
これらは線の太さが結びつきの太さを表わす。(w=「重み」が大きい。wχ=y)
上の図は平面でもわかるけど、つながりが分かりにくい。
下の図はつながりがわかるけど、平面で表すことが難しい。3次元でも同じ。
こうやってまとめると、今まで「〜をめぐる意味宇宙の地図」を描いてきたことは
「意味のネットワーク」であり、「脳内のネットワーク」であることに気がつく。
つまり、紙の上のNNなのだと。そして、その地図によって、新しい課題が見つかり追求していくことができることにも。
これは、知識の「表現」にあたる。
そして、こうやって書くことで「伝達・利用」をはかる。
そして、意味ネットワークは「知識獲得・協働」なのだ。
この意味ネットワーク(紙の上のNN)の働きは未知の課題を見出し、挑んでいくことにある。それこそ脳のやってきたことなのだ。
2、Rのパッケージ「nnet」を使う
「R」という統計処理のとても便利なソフトがある。
これは無料で使えるソフトで、ネットに解説も沢山あり、使ってみようと決意して、昨年来試みている。
使っているとわかるのだけど、すべて巨大な行列で計算をしている。
このRで、しばらく重回帰分析や主成分分析、テキストマイニングなどで遊んでいたのだけど、そのRの中に「nnet」という3層のNNのパッケージがあることを知った。
これを使えば簡単にNNを体験することができる。このnnetにいろいろな値を入力して、どんな出力がされるか確かめてみることで、その働きがわかるはずだ。
さっそく試す。何を入れようか迷ったけど、サイン関数で試すことにした。
学習するデータは、入力が10個で、出力はサイン関数。図にすると下のグラフ。
input output 学習データ(sin9.csv)
1 0.025 0.4530697
2 0.125 0.2878680
3 0.200 0.2146830
4 0.300 0.2146830
5 0.400 0.3236644
6 0.475 0.4530697
7 0.550 0.5927051
8 0.650 0.7427051
9 0.800 0.7853170
10 0.975 0.5469303
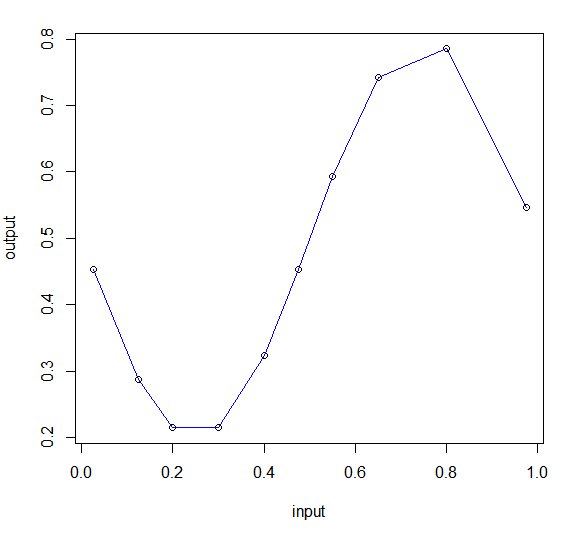
グラフの線はわかり易いように結んだだけでデータには無い。かなりばらつきがあるので、このデータからサイン関数が再現出来たらすごいことだ。
3、シグモイド関数
ここで、ある値域を越えると発火する脳のニューロンの仕組みをモデル化しよう。
ニューロンは多くのニューロンとつながっていて、互いに電気信号を次のニューロンに送っている。ところが、小さな信号にも反応していたらネットが混乱してしまう。
そこで、ニューロンは、他のニューロンたちから来た信号がある一定の値を越えた時に発火して、次のニューロンに信号を送る。
それをモデル化したのがシグモイド関数。
この関数は、ニューロンの発火のモデルの一つで、NNで0か1の値の中間の値を決めるために使われる関数で、確率を表している。
脳のニューロンの働きのように、入力されたxの値(これはプラスからマイナスまでいろいろな値をとる)を0から1までの値に変換して出力する。
例えば、xが−0.5だとすると、yは0.083でほとんど影響を与えない。
この図のa(重み・傾き・太さ)を動かしてみよう。ちなみにこの関数は微分がとても簡単。
4、NNはどんな働きをしているのか・・・バックプロパゲーション
さて、これをNNがどう学習するのかというと、次の図の線の太さ(傾き,重み)を変えて、出力した値が学習データのoutputと一致する様に修正していく。
線の太さは最初は適当にとる。この図でいうとI1は0.025。
線の太さを順にwiとして、かけ合わせてB1(太さは1)と足して、シグモイド関数に入れてH1を出す。
次に、H1からH10までに太さvをかけてシグモイド関数に入れ、それを合計するとO1が出る。
このO1から0.4530697を引くと誤差がわかる。(この時誤差を二乗するのが最小二乗法)
この誤差が0に近付くようにするには、この誤差(の二乗)をwやvの関数とし、それぞれで偏微分するとwやvが誤差に与える影響がわかる。
それを−Δw,−Δvとして仮に与えたwとvに加えていく。
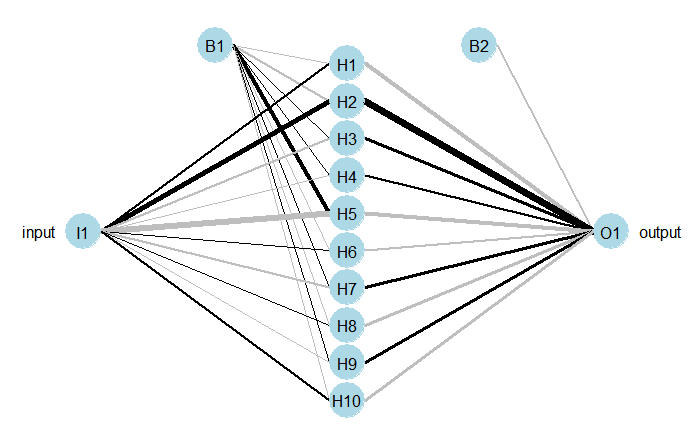
wやvは線の太さを表わす。例えば、I1に0.025を入力すると、f(0.025w1-0.025(=B1))=H1 これをH10まで計算して、今度はf(v1H1+v2H2+・・・+B2)=O1
と計算する。fはシグモイド関数。そして、このO1と0.4530697の差が限りなく0に近づくようにwやv(=線の太さ)を修正していくのがバックプロパゲーション。
これは、手で計算するのは大変だけど、入力した値をNNで計算し、その出力と学習する出力を比べて差の二乗が最小になるように重みwやvを変更していく。
この図のNNはとても単純なネットである。
線の太さは重みの数値の大きさで、黒は正の数で鼠色は負の数だろう。
B1とB2は重み1と決まっている入力。
次に、バックプロパゲーションのイメージ。
出力した値と正答との差が最小になるように中間値を求めれば良い。
そのためには、差を二乗した式が最小になる値、つまりその式を微分して0になれば良い。
このグラフではそれは3か所ある。どうしたら最小値にたどり着けるか?
(スタートを押すと点がどこかへ飛んで行ってしまうので、右上のリセットボタンを押してから再度スタート)
バックプロパゲーションというのは誤差逆伝播法と訳されるが、そのイメージだけでもと思って作成した。
5、Rで実行する
実行したRのスクリプトを書いておく。ちなみにHの数は3にして試してみた。
―――――――――――――――――――――――――――
#バックプロパゲーションによるnnetの学習
library(nnet)
train <- read.csv("sin9.csv",h=T)
train
plot(train)
valid <- read.csv("sin2.csv",h=T)
valid
plot(valid)
#size:中間層、maxit:くりかえし回数 size number of units in the hidden layer. Can be zero if there are skip-layer units.
#それから,predの"type"で出力形式を指定します.通常は"class"でよい
#predic.nnetのhelpより If type = "raw", the matrix of values returned by the trained network;
#if type = "class", the corresponding class
#(which is probably only useful if the net was generated by nnet.formula). weights: 10
sin1 <- nnet(data=train,output~input,size=3,maxit=2000);
yosoku1 <- predict(sin1,valid,type="raw")
plot(valid,type="b")
points(train,type="b",col=2,pch=16)
points(valid$input,yosoku1,type="b",col=4,pch=20)
lines(valid$input,yosoku1,col=4)
―――――――――――――――――――――――――――
#は説明。赤い字がNNのパッケージ。
バックプロパゲーションによってsin1というBBができる。
そこにsin2のxを入力してsin1のyを出したのがyosoku1。
これで結果を出してみると次のグラフになる。
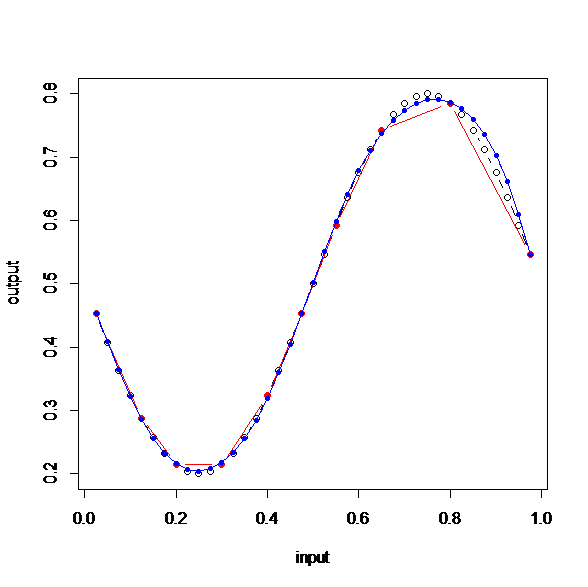
白丸がサインの正しい値(sin2.csvのグラフ)。赤いデータ(学習データ)から青いデータ(nnetからできたsin1)を予測したのだ。
右の上が少しずれているけど、かなり近い。
これはすごいと思う。中間層は3で重みを計算する回数は2000回。
さらに、中間層(size)を10にしてみる(上のNNの図)。
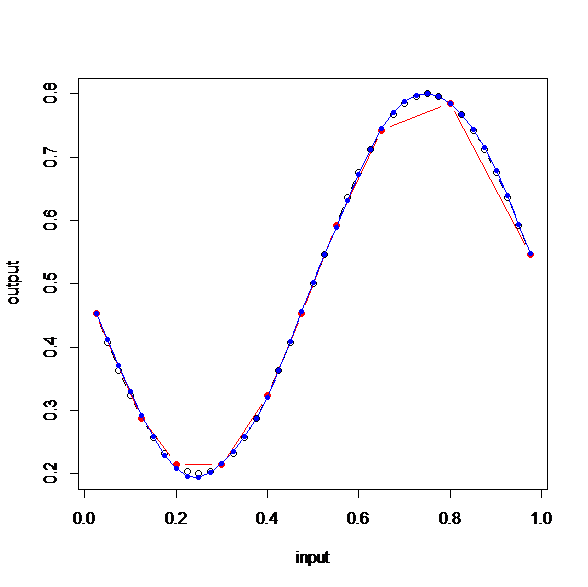
もうほとんどサイン関数だ。
たった10個のデータを与えただけで、サイン関数が再現できたということだ。
これはすごい。
ニューラルネットワーク恐るべし。
6、なぜNNで三角関数が表わせるのか
次は入力層を複数にしたらどうなるのだろう。
線形だったら回帰分析で求めることができるけど、こんな単純なNNなのに三角関数を表わすことがなぜできるのだろう?
これについて、普遍性定理というのがあることを知った。
【ニューラルネットワークと深層学習】
ここにあらすじが書いてある。
「与えられた連続関数をどこまでも近似することができる3層のNNが必ず存在する」
という定理。
これをもっと視覚的にわかりやすく説明してあるのが次のサイト
【初心者向けニューラルネットワークの基礎】
次は、そこからどんな関数でも作れるという原理を考えてみる。
この二つのNNからh−fというパルスを作ることができる。これを沢山集めればどんな関数でもできるはず。
こうやって書いてみるとわからないことだらけ。でも、そのわからない所がわかってくるのがうれしい。
書いてみて感じたことを書いておく。
(1) 「わかる」ということは、古いネットワークと新しいネットワークがつながったときに感じる。
(2) 実際に表現(書く・作る)してみて、このつながりが実感できる。
(3) その時、新しいつながりが見つかればうれしい。
そういう新しいつながりができた時にドーパミンが分泌されるのではないか。
目次へもどる





