地球の公転と日照時間

冬至の後も日の出が遅くなるわけ

　心が落ち着かないので、何か作ろうと考えた。久しぶりにGeoGebraで作ってみよう。
そういえば、冬至を過ぎても日の出が遅くなるのは何故だろうか。 日没の方は冬至の１７日前からすでに遅くなっている。 この表は岐阜市の日の出と日の入の時刻の変化。二日ごとに記録してある。 差も出してみた。→2025年のデータ【日の出日の入時刻】

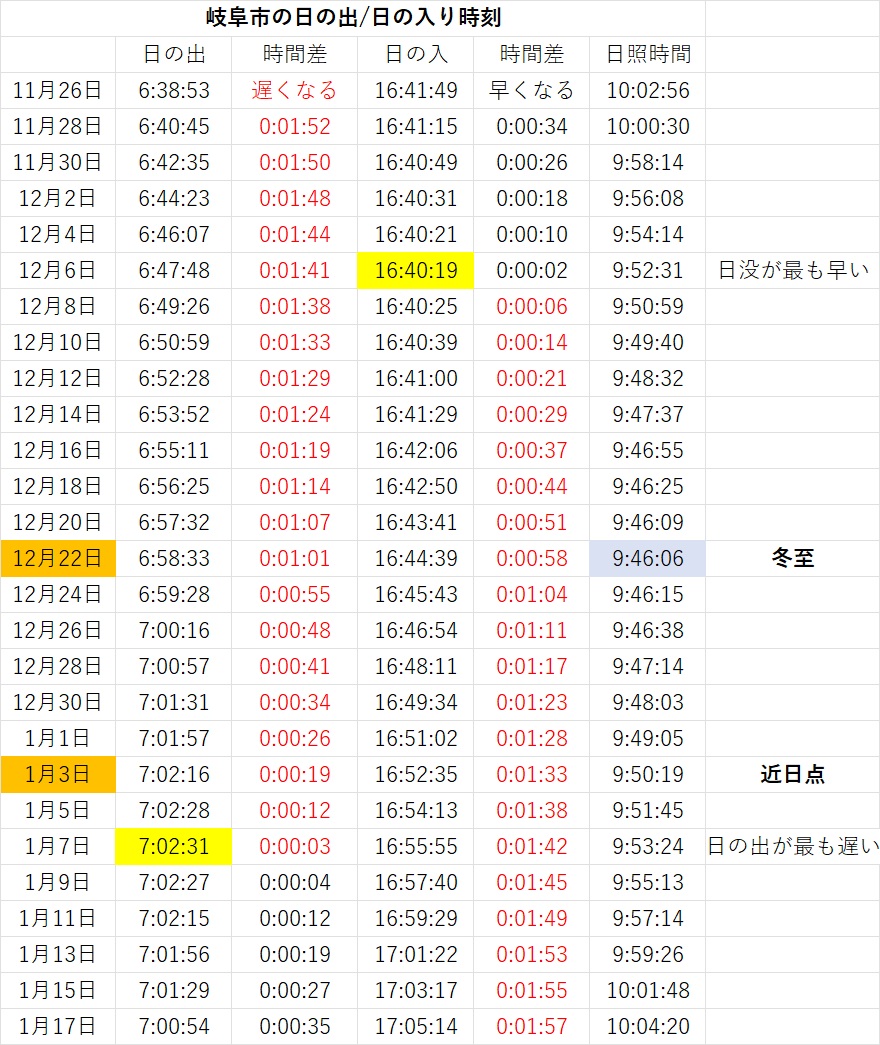
　それは、近日点が冬至の数日後で、近日点では公転の速度が早くなるから。

　近日点では地球は速く動くので、自転の時間に対してより多く進む。 図で日の出と日没（日の入り）を別々に考えてみよう。
　次の図はわかり易くなるように角度を大きくとったもの。 実際は一日で地球が太陽の周りを約１度動く。 しかも驚くべきことに、地球が公転で一日に動く距離は直径の２００倍以上もあった。 そして、近日点と遠日点では動く距離は直径の７倍の距離の差があった。

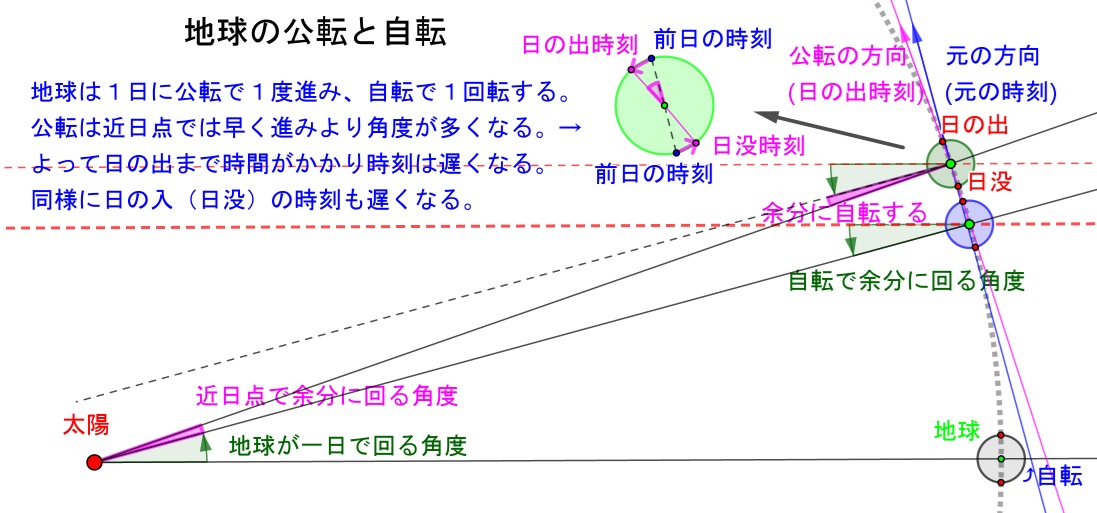
　この図で自転時間は毎日同じなので、回転の位置は同じ。（一日４分のズレは無視する） 近日点では公転はより多くの距離を回る（進む）ので、上の拡大図のように、 前日の日の出の時刻の位置よりも回転しなければならない。したがって、日の出までには時間がかかり時刻は遅くなる。 （私もこれを混乱してしまった。時刻と位置を分けること）
　冬至を過ぎても日の出は遅れて明けるので時刻は遅くなり、同様に日没も遅くなるので時刻も遅くなる。 しかし、日照時間は冬至が一番少なく、もし近日点効果が無ければ冬至以後は、日の出はだんだん早く日の入はだんだん遅くなってくるはずなのに、近日点効果とのズレと競合している。 ただ、日の出と日の入のピークがずれているのはなぜかわからない。

　日照時間の数式については、AIに相談したら次の数式を出したので、それを使い、さらに合うように少し変形した。

基本公式（標準形）

T=215 cos-1(-tanΦtanδ)(時間)\boxed{ T = \frac{2}{15} \cos^{-1}(-\tan\phi \tan\delta) \quad (\text{時間}) }

記号の意味

　どうやって出したのかはわからないが、確かめると正しいようだ。

　次のシートの地球の位置は自由に動かすことができる。北緯も変えられる。 これをいろいろ動かしてみて、内的イメージを構築してみよう。

地球の軌道と日照時間

　地球の公転軌道と北緯３６度の日照時間を表しました。離心率は変更できます。 日数は近日点がスタートです。地球は動かすことができます。北緯も入れてみました。 24時間は白夜、０時間は極夜になります。

　ところで、地球は一日２４時間にするために４分ずつ余分に回転しなければならない。 それは簡単に出せる。 地球は太陽の周りを一年かけて回るのだから、３６０度÷３６５日で、一日に角度で約１度回転する。 つまり、２４時間で１度だから、これを分に直すと、一日２４時間×６０分。
これを３６０度で割ると、４分ぶんだけ余分に回転しているということがわかる。
　絶対位置に関しては２４時間ではなく、４分引いた時間で一回転するということだ。
上の図の一日分は１°で、自転でいうと４分だということ。

　なぜ冬至で日照時間が最小になるのかは、地軸の傾きによる。
角度は公転軌道面に対して２３．４度で、常に北極星の方を指している。
この角度が太陽に対して最大になる位置が冬至で、たまたまこの場所。

　次のシートで、北半球では春夏秋冬がどこだかわかってくる。
さらに、αの角度を９０°にすると真横から見たイメージがわかる。

　近日点で早くなるのは楕円軌道だから。その楕円軌道についての図。

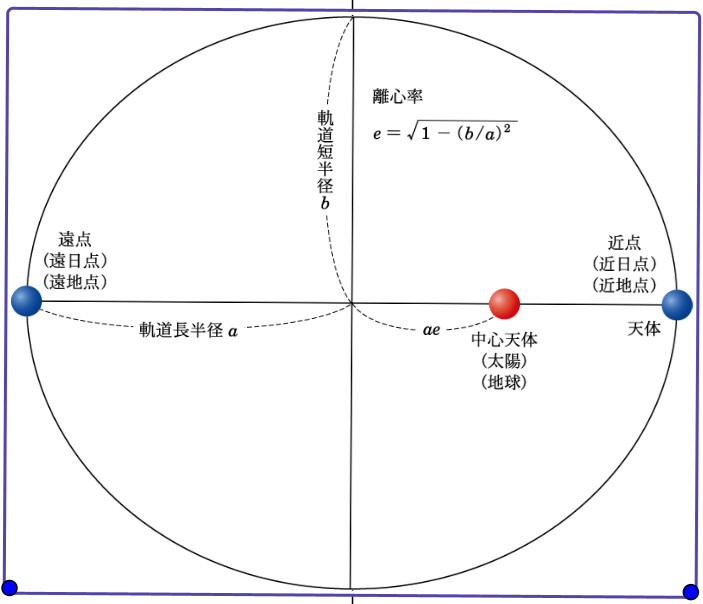
　楕円だと近日点で早くなるのはケプラーが見つけた。

　次のシートは最初の緯度を北緯３５°としてシュミレーションした。
緯度を変化させると仕組みが何となくわかってくる。

太陽の見かけの円が、地平線上にある時が日照時間。
これなら日照時間を計算で出せることが予想できる。
これは昔作ったけど、今見るとこれを理解すること自体が難しいな。
でも、こうやっていくつかのシートを並べるとイメージが膨らむような気がする。

太陽の動き（高度）

　右は地球を固定。左は自分の居る土地から見た図。 この図を作って初めてしくみが分かった。　北極星の高度と緯度が一致することを証明するのも面白い問題だ。　北極や南極での太陽の動きも確かめてみよう。

90－23.4＝66.6　だから北緯66.6度でちょうど太陽が出ない時があることがわかる。
北緯７０度だと白夜もある。

その他の 天体シュミレーション?

AIに聞いてみた。「この日照時間の計算式はどうやって求めたの？」
AIの答え：とても本質的な質問です。
この式は 「地球を球として、天球上の幾何」から 一直線に導かれます。
順にほどいていきますね。

　出発点（考え方の芯）

日照時間 ＝太陽が地平線の上にある間に、地球が回転した角度
　　つまり 角度の問題です。

　　① 天球で考える（図形の舞台）

  • 地球中心を原点とする 天球を考えます。 地平線：天球を切る平面
  • 太陽：赤緯 δ\deltaの位置を回る点
  • 観測者：緯度 Φ\phi 太陽は 赤緯 δ\deltaの小円を 24 時間で1周します。

　　② 日の出・日の入りの条件

  • 日の出・日の入りでは：太陽高度　h=0° 天球の基本公式（球面三角）：sinh=sinΦsinδ+cosΦcosδcosH\sin h = \sin\phi \sin\delta + \cos\phi \cos\delta \cos H ここで、 HH：時角（南中からの角度） 　　日の出・日の入りでは　 h=0h=0： 0=sinΦsinδ+cosΦcosδcosH

　　③ 時角 HHを解く

      整理すると：　cosH=－tanΦtanδ
      ここで H0H_0：日の出（または日の入り）時の時角
    H0=cos‐1(‐tanΦtanδ)

    ④ 日照時間は「この2倍」

    • 太陽は ‐H0-H_0→ +H0+H_0 の間、地平線の上にあります。 よって角度は 2H0

    ⑤ 角度 → 時間に変換

    地球は
    • 360°360^\circを 24 時間で回転
    • 15°=
      1時間
      したがって
    T=2H015T = \frac{2H_0}{15} これに③を代入：

    T=215cos‐1(‐tanΦtanδ)\boxed{ T = \frac{2}{15} \cos^{-1}(-\tan\phi \tan\delta) }

　この計算の仕方が理解できなかったので、具体的にシュミレートしようと考えた。
日があたっている所がわかれば、日照時間を図の中でシュミレーションで出せないだろうか。 面白いシートができたと思う。

北半球を北極星から見た地球です。太陽は左にあります。 地球は左周りに自転しています。 地球の自転と公転は連動しているのでいろいろ試してみましょう。 回転のスピードを変えることができます。

　ところが、シュミレーションする為に交点を求めようと思ったらできない。
そこでAIに聞いたら適切に教えてくれた。
おかげで交点を求めて角度を求めて日照時間を出すことができた。
どうやら私はこういうこまごまとした方法が得意なのだ。

　さらに地図も入れてみた。
少し緯度がおかしいけど、グリーンランドがとても大きいことがわかる。



　　　　　目次へもどる