文字が左右反転しない鏡
― 凹面鏡と凸レンズの研究 ―
1、凹面鏡を作ってみよう
これは、20年以上前にアクリルの鏡で作った放物面の反射鏡です。鏡にして写しました。シャッターを押している手が右手です。手前の赤い線は直線ですが、大きく曲がっています。写した位置は焦点を2倍以上はなれた所です。さて、何かおかしいと感じませんか?



この反射鏡は、二次関数の単元で、平行な光が放物線の焦点に集まることを見せるために作ったものです。苦労して作ったのですが、あまり使いませんでした。【6、ガリレオ と 落体の法則】
最近、これを横にして鏡にすると左右が逆転して映ることに気がつきました。子どもたちに見せても興味を持ちます。
なぜ左右だけが逆転するんだろうか不思議でたまりません。子どもたちも興味を持って、立体視ができると不思議がっています。さあ、いろいろ調べて見ましょう。
Q.1 道路にある凸面鏡は周りが小さく見えます。では、凹面鏡ではどう見えるのでしょうか?
S:凹だから逆に大きく見えるんじゃない。
S:うちに大きく見える鏡があるよ。これって凹面鏡じゃないかな。
T:手鏡で大きく写る鏡だね。確かにそれは凹面鏡ですよ。それがあればすぐにわかるんだけれど、とりあえず凹面鏡を作ってみようか。でも、正確には凹平面鏡だよ。
2、凹平面鏡の作り方
Q.2 エンビの鏡があります。この鏡で(筒型)凹平面鏡を作ります。凹面鏡と比べてどう違うのでしょうか?
まず、作り方。ホームセンターへ行って、アクリルサンデーのエンビ板ミラーを買います。30cm四方で800円ほどで購入できます。エンビですから、簡単に切ったり曲げたりできます。20年でこんなに技術が発展したのですね。


曲げるだけで凹平面ができますが、放物線を描いてダンボールで切り抜き、そこに写真のようにエンビ鏡を放物面になるように曲げて取り付け、セロテープで貼り付けると焦点がわかります。さあ、これを見て確かめましょう。
(なお、焦点をcとすると、放物線の式はy=1/(4×c)*χ^2となります。)
S:あれ?見る位置によって見え方が違うよ。近づけると(横が)大きくなる。だけど、遠ざけるとどんどん大きくなっていって一気に広がり、また小さくなっていく。
S:上下は普通に写っている。
Q.3 凹平面には焦点があります。この焦点内では大きく見えます。そして焦点では無限に大きくなります。では、焦点を過ぎるとどうなるのでしょうか?
S:違いは大きさだけじゃないの?
T:よく見てくださいよ。顔を近づけた時、右目をウインクしてみて。
S:同じだ。
T:今度は顔を遠ざけて、同じ様に右目をウインクしてみて。
S:あれ、反対の目がウインクしている。どうして?
S:左右が逆転しているんだ。
S:それに何だか見にくいな。
3、立体視の原理
Q.4 凹平面鏡では、左右の目に入る像がかなり違います。だから両目で見るとダブって見えます。そこでこれを交差法で立体視します。交差法で見ると、どのように見えるのでしょうか?
S:立体視したら鏡の中が立体的に見るようになったよ。
S:本当だ。手を前にやると浮かび上がって見える。
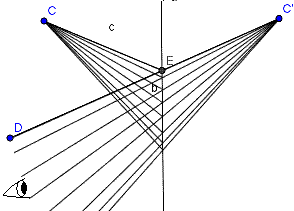
T:その原理はこの図を見るとわかるよ。私たちはこのように反射する物を見ているので、遠近がわかるんだ。
Q.5 縦にするとするとどうなるのでしょう?
S:縦にしても変わらないと思うな。
S:あれ?縦にしたら上下が逆になったよ。世界が逆さになっている。どうしてだろう?
S:左右が逆になると同じ様に、上下が逆になったんだ。
S:ということは、放物平面ではなくて放物面鏡だったら、上下左右が逆転するということかな。
S:それだと、普通のレンズを焦点より外で見るのと同じことだね。
Q.6 文字を映すとどうなる?
平面の鏡は文字が逆転(裏から見た文字)します。では、この鏡で文字を見るとどうなるのでしょうか?
S:右左が逆転した文字が写るはず。
S:あれ?普通の鏡は左右が逆転しているから、それが逆転するということは・・・


S:そうか。元にもどるんだ。書いてあると同じ様に見える。鏡文字ではない。
S:ところで、前にある直線は途中で曲がっていますね。
S:それに、左から見ると、途中で変な所がある。文字が逆転する所があるよ。


S:本当だ。普通の字と鏡文字に分かれて分離している。
S:下の直線も気になるな。なぜ左右だけが逆転するんだろう?
4、左右逆転のヒミツ
Q.7 この鏡を使うと、左右逆転していない自分が向こうにいる。右手は右、左手は左。すると普通の鏡はなぜ左右が逆転しているように見えるのだろうか?
S:そういえば、鏡がなぜ左右逆転するか不思議だよな。
S:この鏡のように上下は逆転しないのはなぜ?
Q.8 凹平面鏡はなぜ左右が逆転して見えるの?
T:では、それを調べてみよう。
S:どうやって調べるんですか?
T:鏡を反射した光がどんな道をたどるのかが分れば理由も分るんじゃないかな?
S:ではどうやって光の道をたどるんですか。光を当てるの?
T:こういうときに便利なのがコンピュータ。
S:ところで、光ってどうやって反射するんだったっけ。
T:では、光の反射と屈折について確かめておきましょう。
ここで素敵なソフトを紹介します。
反射や屈折のシミュレーションをする時に、簡単に作図できるソフトを見つけたのです。
【GeoGebra】というソフトです。
これは、ちょうど「ファンクションビュー」と「GCWin」を合体させたようなソフトです。作図が簡単で、式と表も使えます。
まずは、実際に動かしてみましょう。(Javaをインストールするため初めての方は時間がかかります。)
【光の反射と屈折のシュミレーション】GeoGebra
なお、光の反射や屈折についての理論(最小原理)は、【アリスの水くみ】を参照してください。
S:これを使えば、放物面の反射も分るのですね。
T:そうです。では、放物面鏡の反射についてシミュレーションをしてみよう。
【放物面鏡の鏡像のシミュレーション】GeoGebra
T:Fは焦点。視点をBとすると、鏡像は下の方に見える。Bの周りの物は、見る方向によって位置がずれている。特に、鏡の位置と実際の位置が、左右逆転している所に注意してほしい。Fの少し上に光線が集まる点がある。
Bの位置も動かしてみてください。
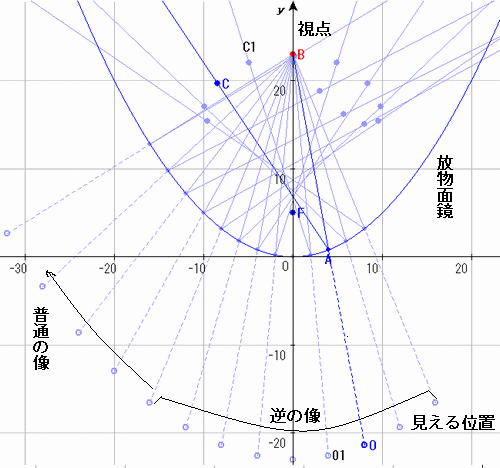
S:なるほど、確かに右へ行くと左へ行く所があるよ。でも、それはなぜなんだろう?
S:焦点で光が集まるんだから、一点から出た光が焦点の付近で集まる。だからそこからは左右が逆になる。
S:でもシミュレーションを見ても、一点に集まっているわけではないよ。
S:見える位置がリボンのようになっている。リボンの先が文字が逆転した所なんですね。
T:そうですね。そこから先は、普通の鏡と同じ様に鏡文字になっています。
S:放物面鏡では、写らない所があるんだ。
Q.9 3−Dミラスコープの仕組みはどうなっているの?
5、実像と虚像
T:今回どうしても欲しくなって「3−Dミラスコープ」1250円を買いました。二つの放物面鏡でできていて、中に蛙が入っており、これが浮かび上がってくるのです。
S:本当だ。この蛙つかめそうな気がするけどつかめない。これって虚像ですか?
T:幻だから虚像と思うのはわかるけど、これは実像です。



S:右側のは何ですか?
T:これは、ミラスコープの平面版。凹平面でも浮かび上がった像が見えるのかを確かめようと思って作ったもの。
S:ちゃんと浮かび上がったんですか?
T:中に豆電球を入れます。そして両目を鏡に沿って見たら(鏡を横にして横に見る)浮かび上がって見えました。やっぱり、両眼視差が大事だということがわかりました。
S:ところで、なぜ3Dに見えるのかがわかりません。
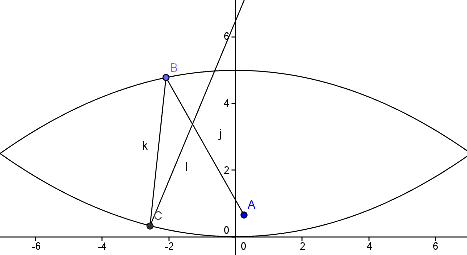
T:それは、この図を見てください。Aから出た光は上の鏡にBで当たって反射し、下の鏡にCで当たってさらに反射します。
S:2回反射しているのですね。
T:Aからは四方八方に光が出ています。その光は上の放物面鏡にも当たります。それはまた反射して下の放物面鏡に当たります。それがさらに反射して上の穴に届きます。そして一つの点Qに集まります。Aが一つの点に集まれば、どこから見てもAがQにあるように見えます。
これを、実際に「GeoGebra」で体験してみてください。
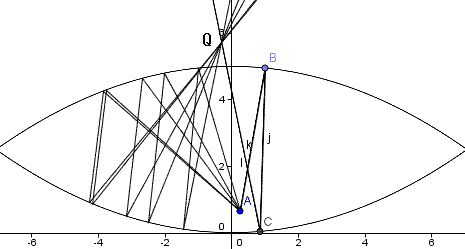
【3-Dミラスコープの実像のシミュレーション】GeoGebra
S:中にある物のそれぞれの位置のから出た光が、ちょうど点対称の位置で再び集まるのですね。
S:それぞれの位置から出た光が一つの点に集まるから、立体視できるんだ。
≪ソフトの作り方≫
Bにおける法線(接線の垂線)を作り、法線に対するAの鏡像を見つける。Cについても同様。なお、焦点はそれぞれの放物線の中心(原点)になっている。放物線の式はy=1/(4・p)χ^2 。pが焦点。
Q.10 実像と虚像の違いは?
S:これが実像だとしたら、凸レンズでも(スクリーンが無くても)立体的な実像が見えるはずだけど。
T:そうです。光が一点に集まったら実像が出来て、立体的に見えるはずですね。実際にやってみましょう。凸レンズを用意して、周りを暗くして豆電球をつけると、浮かび上がって見えるはずです。
S:小さいけど、見えますね。ただし片目だとダメです。両眼で見ると立体的に見えます。
S:レンズを大きくすればミラスコープのように大きく見えるはずですね。
S:レンズの場合も、放物面鏡と同じ様に一点から出た光はレンズのいろいろな位置を通ってまた一点に集まっているのですか?
T:さっそく「GeoGebra」でシュミレーションをしてみましょう。レンズの場合は屈折で光線が曲がります。屈折の角度はスネルの法則によって表で求め、それを図の中に反映させるようにしました。たぶん曲面によって屈折角も違うはずと考え、まず、球面で確かめてみました。どうでしょうか。一点からいろんな方向に出た光が、再び一点に集まるでしょうか。
【球面レンズの屈折と実像のシミュレーション】GeoGebra
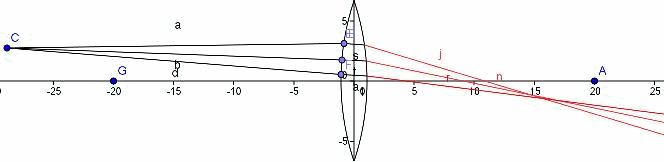
S:ほぼ集まっていると考えてみいいのかな。
S:でも、このシミュレーションは位置によっては一点に集まりませんね。
S:そもそも、平行な光線が一点に集まっているのかな? 試してみよう。
・・・
S:あれ?一点に集まっていない。レンズの場合も放物面でないと一点に集まらないのかな?
T:今度は放物面にしてみましょう。
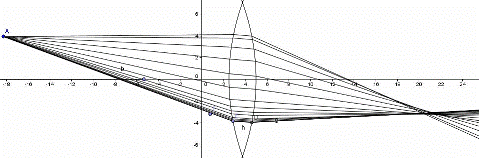
【放物レンズの屈折と焦点のシミュレーション】GeoGebra
S:球面よりは良いけど、放物面でも焦点にきれいに集まりませんね。
S:どんな面だったら焦点にきれいに集まるのでしょうか?
T:これは研究すると面白いかも。でもね、人間の目は多少の誤差があっても修正してしまうから、暗いところで普通の凸レンズを使って像を写すとちゃんと立体視できます。ただ小さくなってしまうからミラスコープのように大きくは見えませんが。
6、まとめ
○虚像はスクリーンを動かしても像を映すことがない。実像はスクリーンを動かすと像をはっきり映すことが出来る。しかし、実像はスクリーンが無くても立体的な像を映すことができる。
○ニュートンの反射鏡は、凸レンズと凹面鏡が同じ働きをするということを見つけた優れた発見だ。
○実像は両眼視差によって立体的に見ることができる。
○物を見るときに大切な見方は、一つの光が届くと考えるのではなく、光の束が目に届いていると考えた方が正しい。
○収差が無いレンズの形は思ったよりも難しそう。
参考文献
【球面鏡と放物面鏡の光線の集まり方の違い】
【「鏡の中の左利き」― 鏡像反転のなぞ】
目次へもどる


















