鏡（テーパー万華鏡）で探る正多面体
１、正多面体万華鏡
S：先生が以前見せてくれた多面体が見える万華鏡を作りたいんだけど、どうやって作るの？
T：もう忘れちゃったよ。それにあの万華鏡はみんなにあげたから手元には一つもない。
S：今、正多面体の勉強をしている。その時に、これ前に見たことがあるぞと思い出して、どうやったら万華鏡が正多面体になるのか知りたいと思ったんだ。
T：ちょうどいい。一緒に考えてみようか。それに前に作ったのは塩ビミラーだったけど、この前ポリカーボネイトミラーをネットで注文したから、それを使って作ってみよう。
（塩ビミラーは少し湾曲しているけど、ポリカーボネイトミラーは平面）
２、鏡は面対称
T：まず、正方形の鏡二面を合わせてみよう。
S：この鏡の角度をいろいろ変えると面白いことがわかってきますね。９０度で平面（２面）。６０度で６面になる。
５面になるのは何度だろう？
T：では、さらにもう一枚鏡を加えて、空間座標のように互いに直角になるようにすると？
S：三面鏡ですね。ここに何か置くとどうなるのだろう？
全部で８個見えますね。
T：ここに（写真）正三角形を描くと、どうなると思う？
S：すごい！ 正八面体だ！ 正八面体の骨組みが立体的に見える。
T：本当に正三角形が８つあるの？
S：さっき、８個見えたから間違いないです。それに、ここにサイコロを置くと・・・
この様に、８つのサイコロが見えます。
T：では、この正八面体の中心はどこにあるのだろう？
S：もちろん、この三面の鏡の交わっている所です。８つのサイコロの中心も同じです。
T：じゃあ、この３面鏡の中心から、同じ大きさの直角二等辺三角形を切り落とすとどうなるのだろう？
S：もしかしたら、正八面体のテーパーの万華鏡になるのですか。
・・・やってみよう。
カッターで２・３回切れば切断できますね。
できた！ 鏡が対称面だから、この角度が同じ（４５＋４５＝９０）になります。
模様を入れると・・・ きれいですね。
３、正八面体から正六面体へ
S：よし、次は正六面体だ。同じように考えると・・・
今度は二等辺三角形が４面が必要ですね。
T：四角錐にするということですね。どんな二等辺三角形になりますか？
S：えーと、一辺を２の正方形とすると、ピタゴラスの定理を二回使うと・・・
中心から頂点までの長さは、√３です。
T：つまり、一辺が２で二辺が√３の二等辺三角形の鏡を４枚張り合わせて、正方形を切り抜けば六面体が見える万華鏡ができるわけですね。
S：でも、四角形ではつぶれるし、先生が見せてくれた万華鏡は切り口も三角形で、３面でした。
T：そうですね。この原理でいくと、正１２面体は５面も必要となりますから、あくまで３面で考えましょう。
S：切口を三角形にするためには、どうすればいいのですか？
T：さっきの正八面体に戻りましょう。この正三角形を半分に切ったらどうなるでしょう？
S：そうか、鏡を９０度から４５度にすれば、面と鏡は垂直になるから一つの平面になる。
T：さっきよりも尖った三角錐になりましたね。この下の面はどんな三角形になるのだろう？
S：４５度の三角形だ。この３つの三角形で三角錐を作って、全く同じように頂点を切ると正８面体ができるわけか。
S：そうすると、正三角形の中心（垂心）で一面を三等分することもできるわけですね。
T：そうです。そうすれば三角錐の万華鏡になります。
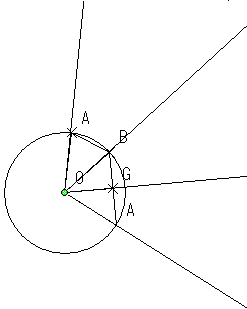
S：計算は、一辺を√２とすると、中心から頂点までは１。中心から三角形の中心（重心＝垂心）までの距離は、√３／３。（下図↓）
ABGOの三角錐を作って、Oの周りを切り抜けば良いわけですね。
設計図は真ん中の図。
これを拡大して、Oの周りを２㎝にして切り取れば出来上がり。三角錐の大きさは１０cmほどが適当。
さあ、覗いてみよう。
計算通りだと嬉しくなりますね。
S：次は正六面体だ。まず、この四角形の対角線を結んで三角形を作る。サイコロの中心から一つの三角形の頂点までの距離を計算すれば良いわけだ。
ABGOの三角錐を作り、△ABGを切り取る。
設計図は右上図のようになる。長方形は切り抜く部分。三角錐の大きさは１０cmほど。
T：二つの直角三角形と一つの二等辺三角形を組み立てて切り抜きます。
S：この直角の所は中心とGが垂直になり、３つの三角形が一つの平面になるのですね。
４、正２０面体
S：よし、この調子で２０面体に挑戦だ。
S：まず、この一面のまま設計図を作ってみよう。
正２０面体の中心から頂点までの長さはどうやって求めるのですか？
T：次のサイトを見てください。⇒【正20面体の頂点座標の求め方】
S：なるほど、黄金比が出てくるのですね。
一辺を２として、中心と頂点までの距離を求めると、√（φ×φ＋１）＝1.9021…
φ＝（√５＋１）／２＝1.618
正三角形になるかと思ったけど、違いますね。
T：これはこれできれいだけど、やっぱり今までと同じように正三角形を三等分してみましょう。今度は三角形の中心(垂心）までの距離を求めなければならなくなって計算が大変。
S：でも、ピタゴラスの定理を知っていれば必ず求められますよ。・・・
設計図は
５、正１２面体
S：今度は正１２面体だ。中心はどうやって求めるの？
T：正１２面体は、正２０面体の頂点を切ったものなんだ。
S：サッカーボールと同じということ？
T：そう。サッカーボールの五角形をもっと大きくし、六角形を無くすと正１２面体になる。
だから、正２０面体を元に計算すれば大丈夫。
今度は五角形を垂心で５等分するよ。
設計図
６、正四面体
S：こうなると正多面体を全部そろえたくなる。正四面体も作ろう。
S：どう三角形を作るかで、いろいろな三角錐の作り方がありますね。
最後に万華鏡の動画。まず、正６面体。
次は、正１２面体。
------------------------------------------------------------
参考サイト
立命館高校の木下侑香里さんの研究｛鏡像による多面体の作成）
http://izumi-math.jp/sanae/Rits11/another/Mirror/Mirror_JSEC/h_right_bottom.pdf
材料は、ホームセンターで「塩ビミラー」だととても安く手に入ります。
５００円ぐらい。
カーボネイトは１３００円ぐらいで、送料込みで１９００円。
目次へもどる