S:共分散を求めるのに2つの偏差をかけ合わせたから、今度は2つのそれぞれの標準偏差をかけ合わせて割ったらどうかな。
S:身長と体重なら共分散は㎝×kgだから、それを標準偏差㎝×kgで割れば単位の違いは無視できるね。
S:それにこの割り算の値は1よりも小さくなる。
(下のシートの式を見ると、Sxy≦(Sx・Sy)だから、Sxy/(Sx・Sy)≦1)
不等式の拡張『相加平均≧相乗平均からコーシーシュワルツの不等式まで』
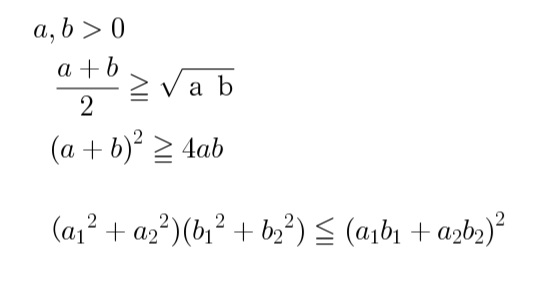
分散から共分散へ、そして相関係数へ
統計を体験する
統計分析では共分散という値がたびたび出てきます。
この共分散という値は、データ分析で威力を発揮するのです。
特に、二つ以上の事柄の相関関係を数値としてはっきり示します。
この共分散の求め方や考え方を調べてみましょう。
最初に、普通の「分散」を体験します。この図はyの数値だけのグラフを横に並べたものです。
S:この図の右と左の二つのデータは、平均は同じだけど散らばりぐあいが違うんだね。
S:この散らばりぐあいを数値で表すにはどうしたら良いのだろうか?
S:散らばりぐあいは平均との差で分かる。
S:だけどマイナスもあるから差し引き0になってしまう。マイナスをプラスにするには2乗すればいい。
S:マイナスの符号を取れば良いと思うけど、なぜ2乗するの?
S:ピタゴラスの定理では距離を求めるのに2乗して足しているよ。
S:そうか、三次元だったらそれぞれ2乗して足して平方根を取っているね。4次元でも5次元でも同じだよね。
S:それで、標準偏差は平方根を取っているんだ。それに分散は図には表せないけど、標準偏差は図の中に示すことができる。
S:つまり、この図の標準偏差は距離の相乗平均ということか。 (a+b)/2≧√(a^2×b^2)
次の図は、Aというデータにはx座標とy座標の二つの値があります。それらの分散はどう考えたら良いでしょうか?
①例えば、Aさんの(英語)と(数学)の点数を平面上の点として表すことができます。
S:テストの点数なんだね。
S:身長と体重でもいいんでしょ。
S:気温とアイスクリームの販売数でもいい。
S:英語の点数が高い人は数学も高そう。
②五つの点ABCDEの分布(散らばりぐあい)がどのようになっているのか調べるには?
S:だいたい右肩上がりの傾向がある。
S:このグループの二つの性質には相関関係がある。
S:それを数値で表すにはどうしたら良いの?
③ これらの点は自由に移動でき、シュミレーション(体験)することができます。
S:数学はできるけど英語は苦手という人もいるから、
S:右下がりになることもあるよ。
S:団子みたいにかたまることもある。
④ そういう性質の違いを何とか数値で表すことができないでしょうか?
S:まず、英語なら英語の平均点aを求める。数学の平均点bも求める。
S:平均点が基準になるね。これで線を引くと4つに仕切れる。
S:この平均点との差が大事なんだ。差(偏差)を求めてみよう。
S:差には±があるから二乗して足して平均を求める。(これが分散)
S:そうすると、英語の場合と数学の場合の散らばり具合の違いが分かる。
S:分散の平方根を取ると標準偏差だ。
S:確かにそれぞれの散らばり具合はわかるけど、この全体の散らばり具合(分布)はどうやって求めればいいのだろうか?
S:英語と数学の偏差をそれぞれ2乗するのではなく、代りにかけ合わせたらどう?
⑤ それぞれの分散は1つの偏差を2乗したけど、2つの偏差を掛け合わせるとどうなるのでしょうか?
S:まず、2つの偏差をかけ合わせたらどうなるか調べてみよう。点Cを動かしてみると、プラスになる時と-になる時がある。
S:xもyも正の時と両方とも負の時はプラスで、どちらかが負の時はマイナスだ。
S:中心から離れると値が大きくなる。この値は散らばり具合をうまく表している。
S:だとすると、5点の平均を求めるとどうなるんだろうか?
⑥ これを分散の時のように全部足して平均を出してみましょう。
S:表計算でやった方がわかり易いね。
S:まず、平均がプラスかマイナスかでどこに分散しているのかわかる。
S:二つの平均がそれぞれx軸とy軸のようなものだから、全体の傾向がわかる。
⑦これを両方の数値を含んでいるので共分散といいます。
S:団子状にすると、値は0に近くなる。
S:直線状に持っていくと共分散は大きくなる。
S:この共分散の値はまちまちだから、標準偏差みたいな基準が欲しいな。
⑧ この 共分散をさらに加工してわかり易くしたいのですが。
S:共分散を何かで割って最大値を1にすればいい。
S:共分散を求めるのに2つの偏差をかけ合わせたから、今度は2つのそれぞれの標準偏差をかけ合わせて割ったらどうかな。
S:身長と体重なら共分散は㎝×kgだから、それを標準偏差㎝×kgで割れば単位の違いは無視できるね。
S:それにこの割り算の値は1よりも小さくなる。
(下のシートの式を見ると、Sxy≦(Sx・Sy)だから、Sxy/(Sx・Sy)≦1)
不等式の拡張『相加平均≧相乗平均からコーシーシュワルツの不等式まで』
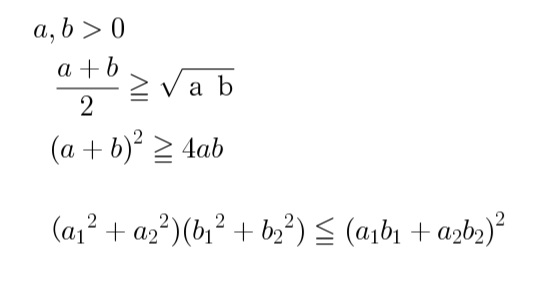
⑨ これ(分散÷(xの標準偏差×yの標準偏差))が相関係数で、-1から+1までの値を取るので見やすくなります。
S:相関係数0.9はかなり直線に近いよ。つまり、相関が大きい。
S:0.5だと少し関係しているかという感じ。
S:この係数によって全体の傾向がどうなっているのかつかめるね。
S:マイナスの場合は相関が逆になっているんだ。
⑩ 相関係数は傾きも表しているから、これらのデータに最も近い直線を表せないでしょうか?
S:この直線は必ず平均の交点(中央)を通るはず。
S:だから後は傾きが分かれば引ける。
S:傾き=共分散÷xの分散で求まる。共分散というのは色々な意味を含んでいるんだな。
これを回帰直線といいます。
(上図により、Sxy/Sxx=Sy/Sx=傾き)
⑪ 三次元でこれを考えるとどうなるのでしょうか?
S:発展とは拡張することだからね。
S:我々を常に拡張せよ!