三角形の「心」から極点・極線へ
三角形の極線と内接二次曲線のつながりを探る
1、三角形の極線と三角形の心
極線のことを調べてみようと思ったのは、
三角形の「心」を調べていると、心がオイラー線や外接円・9点円の周上に並ぶことが確認でき、
さらに一直線上に並んでいる所があると気がついた時に、
この線は何だろうと疑問を持ったのがきっかけだった。
結論を先に言うと、この線は内心を極とする極線。
下の図で確かめてみよう。
n1は三角形の中心を変えて極線(赤)を求めるスライダー。
(三角形の心には番号がふられており、X(1)は内心、X(2)は重心、X(3)は外心、X(4)は垂心、・・・)
nは心を表わすスライダーで、一度に3053個まで出せる。【三角形の心】
いろいろ試していると、なんと極X(648)の極線はオイラー線になっている。
まず、nを3053にしてみよう。3053個の「心」が出てくる。
見ると、たくさん並んでいる所がある。この緑の線はオイラー線で、その上に多くの心が並んでいる。
次に、n1を1(=内心)にしてみよう。
すると、内心を極とする極線が出てきて、その上に心が多く並んでいることがわかる。
2、極と極線
ここで極線の作り方を説明しておこう。
極Iを最初に作って、頂点からIに直線を引いて(ピンク)、対辺との交点を直線(緑)で結び、各辺との交点を求めると、一直線上(赤)に並ぶ。
この赤い線が極線。
ただ、なぜこのような線を考えたのかは、後からわかってくる。
極線は極から作られ、オイラー線や内心の極線になるから、極と極線は1:1対応している。
さらに、極線の意味(調和共役点)について→【三角形の極と極線の関係】
3点が一直線に並ぶのは【メネラウスの定理】から。(この定理から全てが出てくる)
ここで大事なことに気がつく。
それは作図の順番だ。
例えば比から作図するのと極線から作図するのは、結果だけ見ると同じ図だけど過程は全く異なる。
例えば極線から極を求める作図と極から極線を求めることは違う。
定理と逆の定理の関係と同じで、作図の過程そのものが大事なのだ。
では、極線の上に極点を持っていったらその極線はどうなるのだろうか。
・・・(左上の□をクリック)
極線MN上の点Dから極線(青)を作ってみる。
Dを動かしてみると、極線(青)はどう動くのだろうか。
・・・
この極線の包絡線は何かを示しているようだ。
極から作った極線、その極線から作った極線が・・・。
なお、Iを三角形の外に出すと、Dが三角形の中に来て、極と極線の関係がよくわかる。
3、楕円に外接する三角形
ここで、なぜこのような極線を考えたのかを考えてみよう。
左の図は楕円(ピンク)を先に描いてから、接線を引いて三角形を作ったもの。
不思議なことに、頂点と接点を結ぶと一点で交わる。
【一点で交わることの証明】その原理として【チェバの定理】
右の図は当たり前の図だが、左との関連でKLMを通り三角形に内接する楕円が描けないものだろうかと思う。
左の図を見ていると【ブリアンションの定理】との関係が気になる。
ブリアンションの定理は【パスカルの定理】の双対の定理で、外接する六角形の対応する頂点を結ぶと一点で会するというもの。
でも、ここには三角形しかなく、六角形は見えない。
ところが、六角形はちゃんとあるのだ。
そのためには、次の課題を考えてみる。
右図の点KLMで△GHIに内接する楕円をどう描けばいいのだろうか?
・・・実はこの作図には極線が必要となる。
極線がこの二つの絵を繋ぐ媒介となっているのだ。
4、△ABCに内接する楕円の作図
三角形の辺上に二点DEを取り、FからGが求める。あと2点を求めれば楕円が作図できる(5点で二次曲線ができるから)。
この時に極線を使う。
まず、BEと極線との交点PとDを結ぶと、AFとの交点Nは楕円上にある。
同様に、PGとDCの交点も楕円上にある。(あと一つの交点は?)
この2点とDEGから楕円を作図することができる。(これは内接円の拡張でとても面白い。)
この作図によって、極線の働きがわかってくる。
そして、楕円の働きから六角形も見えてくる。
ちなみにこの楕円の最後の一つの交点を作図してみよう。
そうすると、この六角形からパスカルの定理も見えてくる。(これも作図してみよう)
そして、ここにできる六角形は(楕円の)外接六角形でもある。→【パスカルとブリアンションと楕円】
外接三角形と「内接・外接六角形」の関係→【楕円の接線三角形と極線について】
5、極線の極線が指し示すもの
極と極線の不思議な関係について少しずつわかってきた。
この図の作り方は、
(1)楕円を作り、
(2)その楕円に外接する三角形の極線(赤)を作り、
(3)その上の点Mの極線(青)を作図する。
すると、その極線は元の楕円に接する直線になる。
つまりこの極線の包絡線は元の楕円なのだ。
(スライダーで作図のし方をたどることができる)
Mを動かしてみよう。(右クリックのアニメーションでもOK)
Mの極線は確かに元の楕円に接している。
つまり、極線の極線は、元になっている楕円を指し示している。
これはすごいことだ。
いろいろ試していると、Mの位置と極線(青)の位置の関連がわかり、接する理由も少しずつわかってくる。
なお、ここで扱ったのは楕円のみだけど、極点から作図すると、全ての二次曲線を描くことがわかる。
【三角形の極と極線と内接する二次曲線】
【オイラー線の内接二次曲線は放物線】
極線とは何か? なぜ極線が大事なのか? つかめてきただろうか。
パスカル線もパップス線もオイラー線も極線であり、そこに二次曲線に外接したり内接する六角形があったのだ。
二次曲線においては、六角形が基本であり、この六角形のパスカル線と三角形の極線が一致するのである。
「三角形の極の作る内接楕円が六角形を作り出し、その六角形は内接していると同時に外接していて、極線に収束している。」
「極線(赤)上の点と楕円と極線(青)の接点は対応している。L―D,U―P,J―E,T―W,K―F,V―Zに。
つまり、極線を無限遠点でつないだ輪をひっくり返すと内接楕円になっている。」
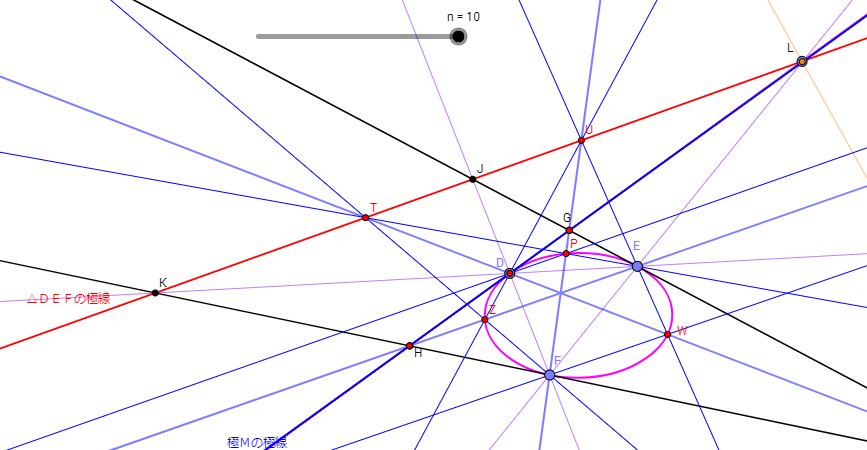
できるだけ単純になるようにまとめたつもりだけど、いろいろ錯綜していて分かりにくいと思う。
でも、これは和算の継承であり、新しい和算の創造でもあると思っている。
もっと詳しく調べるための≪ジオジェブラブック≫
【三角形の極と極線】
【パップスの定理とパスカルの定理】
【円に外接する多角形(証明と作図)作図だけでなく証明を試みました!】
目次へもどる
