S:上下対称のきれいな写真ですね。
T:じゃあこの写真をよく見て。

S:大きな湖があって水面が鏡のようになっている。
S:その湖面には近くの木や遠くの山が映っている。
【問1】これは上下対称?
S:違う。水面の遠くの山が低く見える。なぜだろう?
S:遠近が違うからだよ。遠くの山だと湖面がもっと遠くなるからね。
T:例えば高いところから水面に映った像を見ると、近くの物は下に見える。
S:それは水面が低くなっているからだ。
S:つまり遠くのものほど水面は高くなっている。
S:どういうこと?
S:水面は水平だから遠くになるにしたがって高くなるんだ。
【問2】
S:じゃあ、水面はどこまでも高くなるの?
S:水平線は目の高さだと聞いたことがあるよ。
S:どんな高い山に登っても見える水平線は目の高さということ?
S:そうだよ。見たことある。下の方に水平線があったらおかしい。
S:図にしてみるとすぐにわかるよ。
横から見た図ね。鼠色の線が映った像(写真)だとすると遠くに行くにしたがってだんだん高くなる。
そして、視点の下になっている。
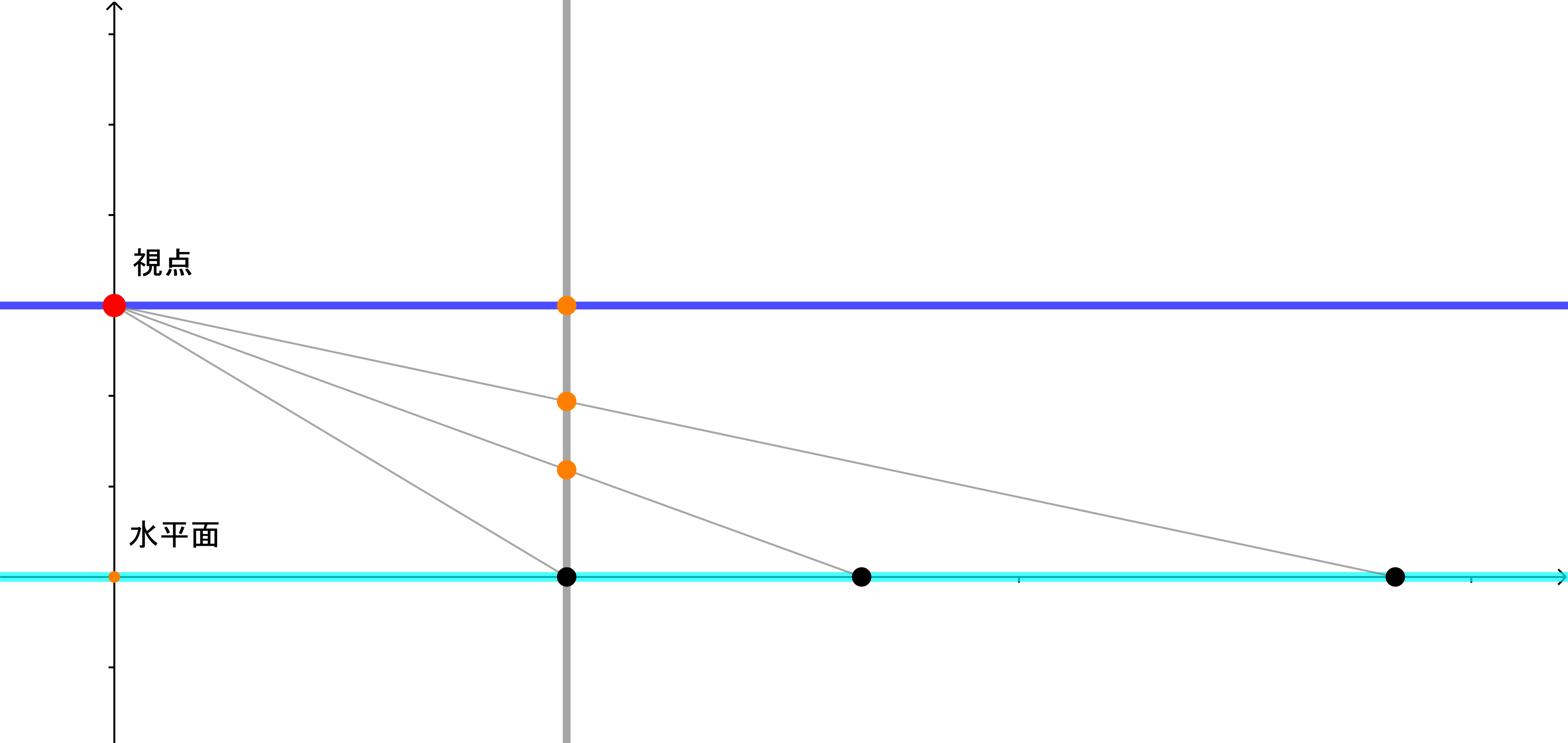
【問3】
S:水面に映る山ってどうやって反射しているのかな?
T:とても良い質問だね。光は最短コースを通るということは知っているね。
S:反射も最短コースをたどるということですか?
T:そうです。次の図のスライダーgを動かしてみてください。
S:なるほど。直線が最短だから、鏡の反対側の同じ位置と直線で結べばいいんだ。
S:これを応用すると、水面の反対側に同じ長さを取って視点と結ぶ・・・。
T:この写真には遠くの山が湖面に映っている。だったら、
【問4】この遠くの山に対する水面の位置を求めることができるのでは?
S:そうだね。鏡と水面は同じと考えると・・・この時、水面は実像と逆像の真ん中にある。
S:これを図で示してみよう。矢印の頂点やGは動かすことができるよ。
S:実際の中点が写真の中点になっていることが不思議だ。
S:中線は中点を通るからだ。
S:実像と逆像の中点が水面ということだね。
【問5】
S:水平線は地球が平面でもできるんだろうか?
S:平行線を考えるとわかるよ。まっすぐな線路は一点で交わっている。
T:Cを動かすと視点が上下するよ。
S:視点が上下しても水平線は変わらないということか。
S:つまり水平線は平面でもできるんだ。
T:地球は大きいから平面と考えても大丈夫。
【問6】
T:影と実物の中点で水面の位置がわかるとすると、水面の高さによって距離がわかるのではないか?
S:なるほど、遠くなれば水面(中点)は高くなるんだから、その比率が距離を表していると考えられるね。
S:問題はその比率だ。そうか、こういう時は単純な図にして調べるんだ。
S:基準になるものと比較するものの距離を比べてみる。その時の中点の位置がどうなっているか?
S:Bは1だからCを2に持っていくと・・・。さらに3にすると・・・。わかってきたぞ。
S:△AJK∽△CJBだ。
S:その比はAK:BC=KJ:JB。
S:もっと言えば、AK:IC=KJ:KB。つまりIC/AK=KB/KJ。
S:これを最初の写真に当てはめてみよう。
S:でもこれでは水平線の位置がわからない。
S:そこが問題だったんだよな。
S:そうだ!水平線の増え方は遠くなればなるほど小さくなるから、一番遠いと思われる山の中点(M)を水平線とみなせばいいんじゃないかな。
S:シュミレートしてみよう。⇒【仮の水平線のシュミレーション】
S:手前にある山は湖の長さの7倍以下の距離にあるということですね。
S:これは鏡があれば他にも応用できますね。⇒【鏡を使って距離を求める】
S:面白かった。
目次へもどる