マクスウェルの独楽 （実験で認識を深める）
コマはなぜ倒れないのか？
子どもの頃から、コマがなぜ倒れずに回りつづけるのか不思議でした。でも、本を読んでも角運動量とか理解できませんでした。ある時、岐阜物理サークル「のらねこ学会」の例会報告に次の文が載っていました。
「植木鉢用の皿にボールペンの軸をつけたコマです。コマの重心がほぼ軸の先端（支点）にあり，重力による力のモーメントを受けないので軸が鉛直でなくても歳差運動することなく安定して回り続けます。（確か〈マクスウェルの独楽〉という名前で呼ばれてたはず）重力の影響を受けないので，力のモーメントと角運動量の変化の関係がよく分かります。」
このニュースを読んで、さっそくこのコマを作ってみました。作って回してみると、確かに歳差運動をすることがなく常に一定の方向を指しながら回っています。実に不思議な気がします。土台を動かしても、向きは変わりません。簡単なジャイロスコープです。
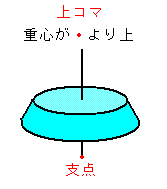
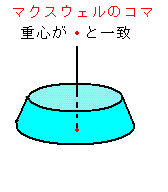
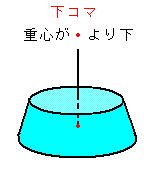
（上の絵をクリックするとそれぞれの動画が出ます。このコマはおもりをつけて重心を調節してあります。この調節が難しい。）
『重心が軸の先端よりも下にあるコマ』
このコマで遊びながら考えたのは、重心が軸の先端よりも下にある場合はどうなるのかということです。ちょうどやじろべえみたいなコマなので、きっと起き上がるコマができると思って作ってみました。
すると、このコマも斜めにまわすとやはり歳差運動をするではありませんか。重心が上にある普通のコマとどう違うんだと考え、普通のコマも作って比べてみました。(動画)
重心が上にあるコマ(上コマ)は、右回しの場合は歳差運動も右回りです（時計回り）。重心が支点にあるコマは、歳差運動をしません。ところが、重心が下にあるコマ(下コマ)は右回しで歳差運動は左回りになります。何と、上コマと下コマは対称になっているではありませんか。
どうしてこうなるのか考えてみました。まず参考にしたのは、次の文です。（エンサイクロペディアから）
------------------------------------------------------------
ジャイロスコープ
たがいに垂直な軸の周りを回転できる３つの輪形の支持台で独楽(こま)のようにまわる回転子をささえ、回転子の回転軸が、３次元のどの方向にも自由にうごくような装置。回転儀ともいう。
ジャイロスコープには、
(1)回転軸が空間で一定方向をたもつ(回転体の慣性)
(2)回転軸に直角な力をくわえると、回転軸は力の方向と垂直な方向にふれる(歳差運動)
(3)歳差運動の妨害に対しては反作用を生じない
という３つの性質がある。
回転体の慣性
回転体の慣性は、ニュートンの運動の第一法則から明らかである。この第一法則によれば、物体が力をうけない場合は、静止していた物体はいつまでも静止し、うごいている物体は等速直線運動をつづけようとする。したがってジャイロの回転子は、１度回転をはじめると、同じ回転面と、ほぼ同じ回転軸で空間の中で回転しつづけようとする。
歳差運動
回転軸に方向をかえようとする外力がはたらくと、外力の方向に対して垂直の方向に軸がふれる。このふれは、回転体の角運動量と、外力をあわせてできた力によっておきる。これを歳差運動という。
歳差運動の身近な例としては、自転車の車輪をまわすあそびがある。輪を回転させて軸の向きを変えようとする場合、その方向におせばよいと思いがちだが、加えた力に対して垂直に回転軸のふれがおきるわけだから、まげたいと思う反対方向にたおせば、輪軸は方向をかえることになる。
------------------------------------------------------------
これを読んでもさっぱりわかりませんでした。ところが、この３種類のコマを回してみると、上コマと下コマは対称であることがわかります。今までコマの運動が分かりにくかったのは非対称であったからです。そして、重力や起き上がる力を受けなければ、マクスウェルのコマのように慣性の法則で同じ方向でいつまでも回り続けようとすることが分かりました。回転体（コマ）の慣性の法則はイメージとしてつかみにくいのですが、こうやって実験してみると、よく分かります
さて、次に重心が上にあるコマ（上コマ）は、どうして倒れないのかと前から不思議に思っていたことを考えてみました。慣性の法則があっても、重力で下に引かれているわけですから倒れてもよさそうなものです。ところが倒れないのは、歳差運動をすることで倒れる向きを常に変えているからなのだろうと思いました。
『では、その歳差運動はなぜ起こるのか?』
重心が下にあるコマ（下コマ）と上コマを比べてみると、歳差運動はまったく逆になります。つまり、まったく逆の力が働いていることになります。上コマは軸を下に倒そうとする力です。では、下コマは？
そうです、起きあがろうとする力が働いているので、軸を上に起こそうとする力が働いていることになります。すると、下に引く力が右に回る力に変化し、起こそうとする力が左に回る力に変化したことがわかります。
そこで「(2)の回転軸に直角な力をくわえると、回転軸は力の方向と垂直な方向にふれる(歳差運動)」ということを考えてみました。なぜ加えた力の方向とは垂直にふれるのでしょうか。そして、その二方向ある垂直の向きはどうやって決まるのでしょうか。
上コマは重心に下向きに重力がかかっています。それとコマの右回りの回転とが絡み合って軸に対して垂直に横ぶれの動きがおきると考えられます。下コマは上向きに起こす力と右回りの回転によって反対の動きが起きるのでしょう。
しかし、２つのコマを比べるからそうなることが分かるのであって、一体どうして、力の方向と垂直な力が起きるのか分かりません。
サイトで検索してみると、【EMANの物理学・力学・コマの歳差運動】に面白いことが書いてありました。
ポイントはコマの「回転体の慣性の法則」です。
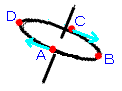まず、水平に回転しているコマには歳差運動は起こりません。斜めに回転している上コマには重心に重力がかかって倒そうとします。回転していなければ倒れます。下コマの場合は起こそうという力が働きます。
ここで、上コマの円周の回転する方向に注目します。斜めになったコマは、Ａ,Ｂ,Ｃ,Ｄそれぞれの回転する方向が違ってきます。ＤとＢは水平ですがＡは斜め上向き、Ｃは斜め下向きです。
重力がコマを動かそうとすると、Ｄ,Ｂは水平に動くだけですから向きは変わっていないので影響を与えませんが、Ａ,Ｃはそうはいきません。Ａにはさらに上に向かそうとする力が働くので、それに反発して下を向こうという反作用が働きます。これがＡを下げます。逆にＣには斜め下に向いていたものをさらに下を向かそうとする力が働くので、反作用で上に向かう力が働きＣは上がります。
そうすると、こちら側（Ａ）へ倒れることになります。これが連続的に起こり、右回りの歳差運動になります。Ａの気持ちになれば、自分の方へ倒れながらだと向きを向きを変えるのが少なくてすむといっても良いのかもしれません。
下コマは全く逆になることが分かります。つまり対称性が見事に説明されてしまうわけです。いや、対称性によって説明されると言った方が良いのかもしれません。
これを実感するには、昔懐かしい「地球ゴマ」を回します。回転させたコマを横に（ＤＢを）持って手前（Ｂの方向）に倒してみると、丁度直角の左側（Ａの方向）へ倒れるのです。向こう側（Ｄ）へ倒すと右（Ｃ）に倒れます。
何回やってみても変な感じがします。まさに、ここで説明した力が起きているのです。こちら側へ倒そうとする力が、左側に連続して移るので歳差運動になり、コマは倒れないということが実感できます。【地球ゴマの動画】（この動きを使った案内ジャイロ"ジャイロ キューブ センサス"が発明されているそうです。【地球ゴマの加工について】）
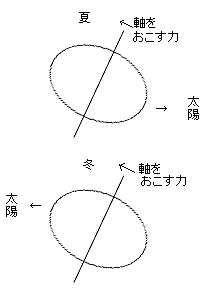『地球もコマ――地球の歳差運動』
さて、次に考えたのは、地球の歳差運動です。地球は北極から見ると左回転(自転)をしながら、2.6万年周期の右回りの歳差運動をしています。これは「下コマ」と同じ運動です。ということは、地球にも軸を起こそうといいう力が働いていることが分かります。
傾いている地球を起こそうとする力とはどういう力なのでしょうか。いろいろ調べましたが、はっきりしたことは書いてありませんでした。私が想像するのに、地球は回転楕円体をしているので、傾いている地球（夏と冬）は太陽（月）の引力で冬の場合は北半球がより引っ張られ、夏の場合は、南半球がより引っ張られるのでそれが地球を起こそうとする力なのではないかということです。
この三つのコマを作ってみて、コマの性質が初めてわかったように思います。実際に物を作って考えるとよくわかります。
もどる