『計算する生命』を読んで
計算と思考
はじめに
幾何の定理（現象）の証明をしていて、補助線を使って証明するとなるほどと思うのに、計算で証明するとそう思わないのはなぜか気になっていた。
計算するのは、考えることを省略しているように感じるからだ。
でも、この本を読んで計算することも思考と同じなんだと感じたので、いろいろ感じたことを書いてみた。
思いつくことをその度にブログに別々に書いていた。
それをまとめようと思ったけど、まとめるとすっきりしすぎて面白くないと感じる。
そこで別々に関連することをまとめてみることにした。
そもそも解析幾何学はデカルトの座標から始まる。
彼はユークリッド原論を学び、そこに厳密で論証的な真理を見出した。
そして、それを自分の哲学にも当てはめようと考えた。
その過程も面白いので図で現わしてみる。
「問題を文字式に置き換えて計算する」という革命はどうやって生まれたのか、それを少しでも明かにできると面白いと思う。
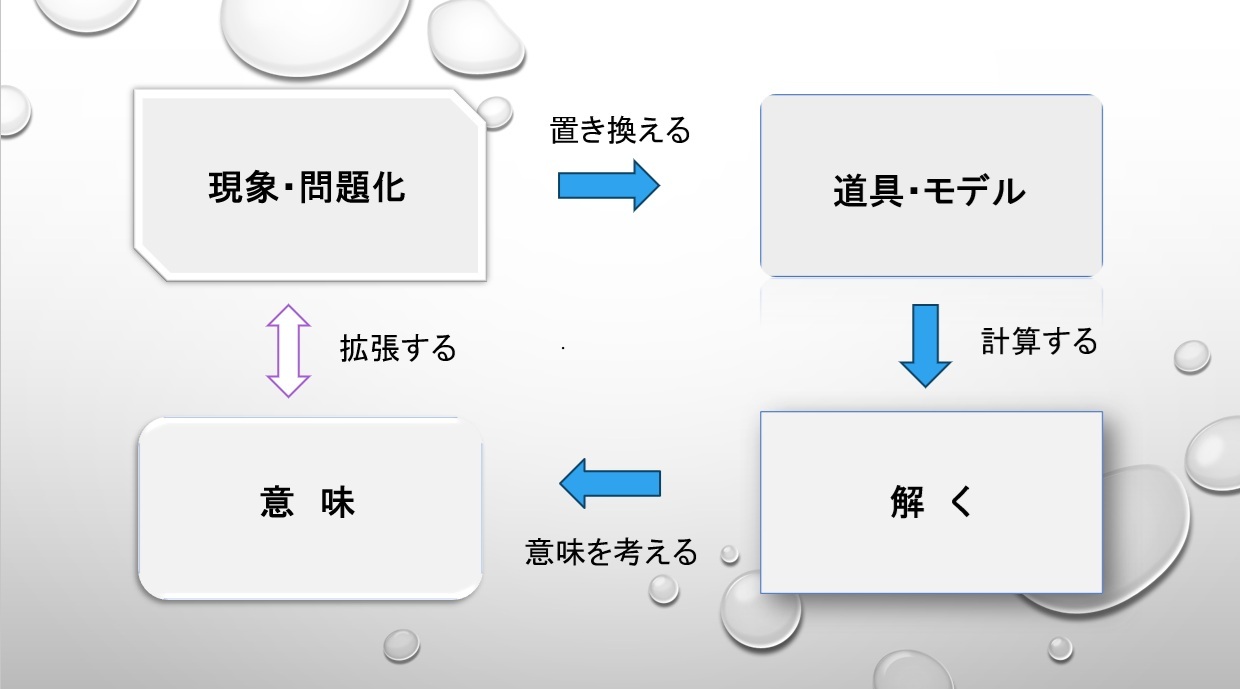
ここで考えたことを「回り道」で表すと次のようになる。
今まで、四つ目の四角を「確かめること」だと考えていたけど、これが「意味を考えること」だと納得した。
つまり、この回り道は答えにたどり着く道だけではなく循環する生命の方法なのだ。
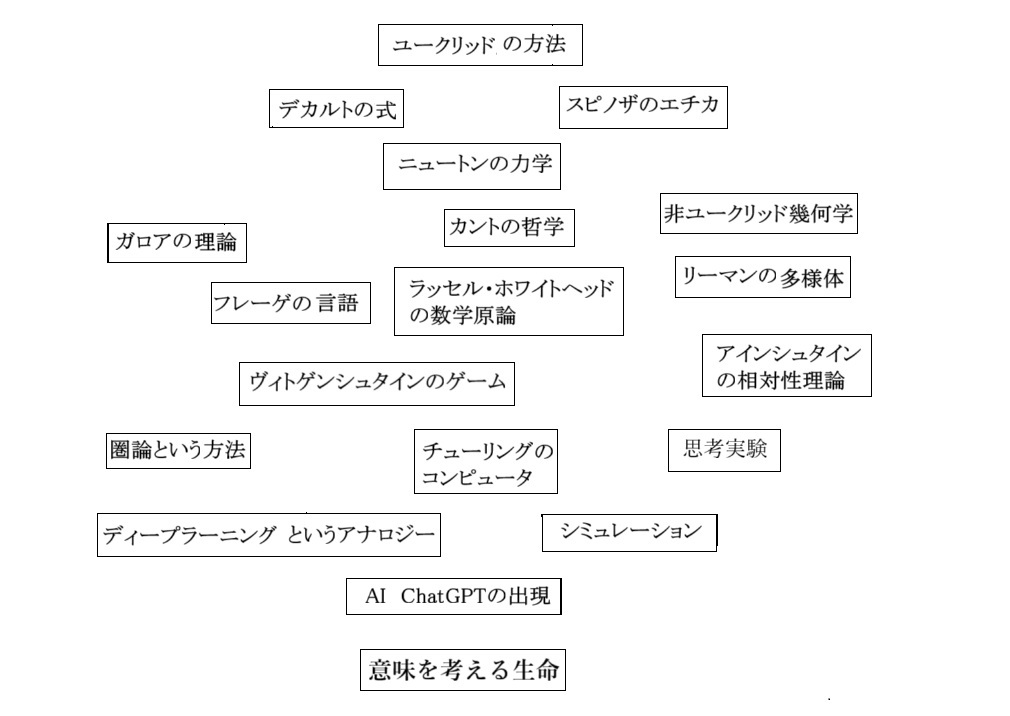
ついでに、AIに至る大きな歴史を図にしてみた。
これを見ると、「ユークリッドの方法」が大きな影響を与えていることに気がつく。
それは、「現象の原理を探り、根本的な定義や公理や法則を探り出していく」というもの。
「ユークリッドの方法」がヨーロッパの学問に及ぼした影響はとても大きい。
ガリレオは「自然の真理は数学で表現されている」と言った。
そして、デカルトは確かな哲学を構築する為にユークリッドの方法を応用した。
現象学の創始者フッサールも数学を研究していた。
①計算と思考
②『計算する生命』
③ネガティブ・ケイパビリティと数学の問題
④「証明」と「わかる」というコト
⑤「認知歴史学」
⑥カントの「５＋７＝１２」について
⑦「鶴亀算」と「式の計算」
回り道の図が一番わかり易いので現わしてみる。
１．ユークリッドの方法
［ユークリッドの方法］ → ［現象の原理を探る］
↓↑ ↓
［原理を生み出す公理］ ← ［その原理を使うと説明できる］
２．問題を解く
［わからない現象］ → ［よく似ている現象に当てはめる］
↓↑ ↓
［元の現象に当てはめる］ ← ［その原理を使うと説明できる］
３．非ユークリッド幾何学
［第五公準は証明できないか］ → ［別の公準にして矛盾を引き出す］
↓↑ ↓
［公準は仮説である］ ← ［どこにも矛盾が出なかった］
４．ガリレオの自然科学
［ 感覚 ］ → ［はかり］ （生活世界）
予見 ↓↑ ↓
［法則の発見］ ← ［計測データ］ （理論世界）
５．アブダクション
［ 現象 ］ → ［ 仮説 ］
↓↑ ↓
［ 意味 ］ ← ［ 検証 ］ 意味を捨象してしまては自然科学や数学は成り立たない
６．フッサールの本質観取の例
［具体的例を挙げる］ → ［その対象や状況の特徴は何か］
↓↑ ↓
［心の動き・条件などを総括的に考察］ ← ［その感情はどんな特徴を持っているか］
７．コンピュータのシミュレーション
［ 複雑な計算 ］ → ［道具を使う（ソロバン・方程式・PC）］
↓↑ ↓
［その結果の意味は］ ← ［途中の計算はわからないけど結果は出た］
目次へもどる